目次
概要
OpenCV で k 平均法 (k-means) を使って、画像の代表色を取得する方法を紹介します。
cv2.kmeans
retval, bestLabels, centers = cv2.kmeans(
data, K, bestLabels, criteria, attempts, flags[, centers])
引数
| 名前 | 型 | デフォルト値 |
|---|---|---|
| data | ndarray | |
| 入力データ。形状が (M, N) の numpy 配列。 | ||
| K | int | |
| クラスタ数 | ||
| criteria | list of int | |
| アルゴリズムの終了条件 | ||
| attempts | int | |
| k 平均法を何回実行するか | ||
| flags | int | |
| アルゴリズムに関するフラグ | ||
返り値
| 名前 | 説明 | ||
|---|---|---|---|
| retval | compactness measure の値 | ||
| bestLabels | 各サンプルに割り当てられたクラスタ | ||
| centers | クラスタの中心の一覧 | ||
criteria
criteria は最大反復回数及び移動量の閾値を 2 通りの方法で指定します。
- 最大反復回数: 反復回数がこの値に達した場合、アルゴリズムを終了する
- 移動量の閾値: 各反復でクラスタの中心を移動するが、この移動量が閾値未満になった場合はアルゴリズムを終了する
attempts
最初、クラスタの中心は適当な点で初期化されるので、アルゴリズムの結果は毎回異なります。attempts に 2 以上の値を指定した場合、アルゴリズムをその回数分実行し、compactness measure の値が最小となる結果、つまり、最良の結果を返します。
retval
サンプルとそのサンプルが属するクラスタの中心との 2 乗距離になります。
サンプルを $\bm{x}_1, \bm{x}_2, \cdots, \bm{x}_N$ としたとき、
$$ \text{retval} = \sum_{i = 1}^N \| \bm{x}_i – \bm{x}_i が属するクラスタの中心 \|^2 $$画像の代表色を取得する
画像で使われているすべての色に対して、$k$ 平均法を適用し、代表色を $k$ 色取得します。
In [1]:
import cv2
import numpy as np
from IPython.display import Image, display
from matplotlib import pyplot as plt
def imshow(img):
"""ndarray 配列をインラインで Notebook 上に表示する。"""
ret, encoded = cv2.imencode(".jpg", img)
display(Image(encoded))
# 画像を読み込む。
img = cv2.imread("sample.jpg")
# 画像で使用されている色一覧。(W * H, 3) の numpy 配列。
colors = img.reshape(-1, 3).astype(np.float32)
# クラスタ数
K = 5
# 最大反復回数: 10、移動量の閾値: 1.0
criteria = cv2.TERM_CRITERIA_MAX_ITER + cv2.TERM_CRITERIA_EPS, 10, 1.0
ret, labels, centers = cv2.kmeans(
colors, K, None, criteria, attempts=10, flags=cv2.KMEANS_RANDOM_CENTERS
)
print(f"ret: {ret:.2f}, label: {labels.shape}, center: {centers.shape}")
labels = labels.squeeze(axis=1) # (N, 1) -> (N,)
centers = centers.astype(np.uint8) # float32 -> uint8ret: 131459173.92, label: (140500, 1), center: (5, 3)
- labels は各サンプルが割り当てられたクラスタを表す (NumSamples, 1) の numpy 配列
- centers はクラスタの中心点を表す (K, M) の numpy 配列
例えば、$i$ 番目のサンプルが割り当てられたクラスタの中心点を取得したい場合は、centers[labels[i]] とします。
In [2]:
# 各クラスタに属するサンプル数を計算する。
_, counts = np.unique(labels, axis=0, return_counts=True)
# 可視化する。
fig, [ax1, ax2] = plt.subplots(1, 2, figsize=(10, 3))
fig.subplots_adjust(wspace=0.5)
# matplotlib の引数の仕様上、[0, 1] にして、(R, G, B) の順番にする。
bar_color = centers[:, ::-1] / 255
bar_text = list(map(str, centers))
# 画像を表示する。
ax1.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB))
ax1.set_axis_off()
# ヒストグラムを表示する。
ax2.barh(np.arange(K), counts, color=bar_color, tick_label=bar_text)
plt.show()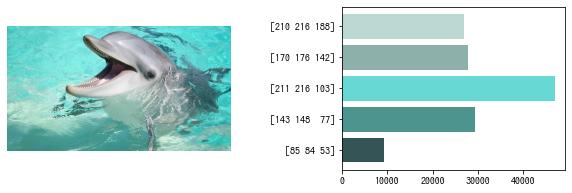
画像の各画素をクラスタの色で置き換える
In [3]:
# 各画素を k平均法の結果に置き換える。
dst = centers[labels].reshape(img.shape)
imshow(dst)



コメント