目次
概要
numpy の複素数に関係する関数について解説します。
一覧
| 名前 | 説明 |
|---|---|
| numpy.real | 複素数の実部を返す。$\Re(z)$ |
| numpy.imag | 複素数の虚部を返す。$\Im(z)$ |
| numpy.real_if_close | 虚部が0に近い場合は実数にして返す。 |
| numpy.conj | 複素共役を返す。$\bar{z}$ |
| numpy.angle | 複素数の偏角を返す。$arg(z)$ |
| numpy.isreal | 要素ごとに実数かどうか判定し、bool 配列を返します。 |
| numpy.iscomplex | 要素ごとに複素数かどうか判定し、bool 配列を返します。 |
| numpy.real_if_close | 複素数型である、または配列に複素数が1つでも含まれる場合は True を返します。 |
| numpy.isreal | 複素数型でない、または配列に複素数が1つも含まれない場合は True を返します。 |
numpy.real
複素数数の実部を返します。ndarray.real と同じです。
numpy.real(val)
引数
| 名前 | 型 | デフォルト値 |
|---|---|---|
| val | array_like | |
| 入力配列。 | ||
返り値
| 名前 | 説明 |
|---|---|
| out | 複素数の実部。型は a が実数の場合は a の型、a が複素数の場合は float になります。 |
In [1]:
import numpy as np
a = np.array([1.2, 3.4 + 5j, 6j])
# numpy.real()
print(np.real(a)) # [1.2 3.4 0. ]
# ndarray.real
print(a.real) # [1.2 3.4 0. ][1.2 3.4 0. ] [1.2 3.4 0. ]
numpy.real_if_close
配列のすべての複素数の虚部が 0 に近い場合は、実数にして返します。
虚部が 0 に近いかどうかは、入力配列の型の計算機イプシロンを eps としたとき、$\Im(z) < eps \times tol$ を満たすかどうかで判定します。
numpy.real_if_close(a, tol=100)
引数
| 名前 | 型 | デフォルト値 |
|---|---|---|
| a | array_like | |
| 入力配列。 | ||
| tol | float | 100 |
| 配列内の虚部の許容誤差をマシンイプシロン単位で指定します。 | ||
返り値
| 名前 | 説明 |
|---|---|
| out | 型は a が実数の場合は a の型、a が複素数の場合は float になります。 |
In [2]:
a = np.array([1.2, 6 + 4e-15j])
print(np.real_if_close(a)) # [1.2 6. ]
# すべての虚部の値が閾値以下でない場合、実数を返さない。
a = np.array([1.2, 2 + 4j, 6 + 4e-15j])
print(np.real_if_close(a)) # [1.2+0.e+00j 2. +4.e+00j 6. +4.e-15j][1.2 6. ] [1.2+0.e+00j 2. +4.e+00j 6. +4.e-15j]
numpy.imag
複素数の虚部を返します。ndarray.imag と同じです。
numpy.imag(val)
引数
| 名前 | 型 | デフォルト値 |
|---|---|---|
| val | array_like | |
| 入力配列。 | ||
返り値
| 名前 | 説明 |
|---|---|
| out | 複素数の実部。型は a が実数の場合は a の型、a が複素数の場合は float になります。 |
In [3]:
a = np.array([1.2, 3.4 + 5j, 6j])
# numpy.imag()
print(np.imag(a)) # [0. 5. 6.]
# ndarray.imag
print(a.imag) # [0. 5. 6.][0. 5. 6.] [0. 5. 6.]
numpy.conj
複素数の複素共役を返します。
numpy.conj(x, /, out=None, *, where=True, casting="same_kind", order="K", dtype=None, subok=True[, signature, extobj]) = <ufunc "conjugate">
引数
| 名前 | 型 | デフォルト値 |
|---|---|---|
| x | array_like | |
| 入力配列。 | ||
返り値
| 名前 | 説明 |
|---|---|
| y | 複素共役 |
In [4]:
a = np.array([1.2, 3.4 + 5j, 6j])
print(np.conj(a)) # [1.2-0.j 3.4-5.j 0. -6.j][1.2-0.j 3.4-5.j 0. -6.j]
numpy.angle
複素数の偏角を返します。
numpy.angle(z, deg=0)
引数
| 名前 | 型 | デフォルト値 |
|---|---|---|
| z | array_like | |
| 入力配列。 | ||
| deg | bool | 0 |
| True の場合は角度を度数で、False (デフォルト) の場合はラジアンで返します。 | ||
返り値
| 名前 | 説明 |
|---|---|
| angle | 複素平面上の正の実軸からの反時計回りの角度で、型は numpy.float64 になります。 |
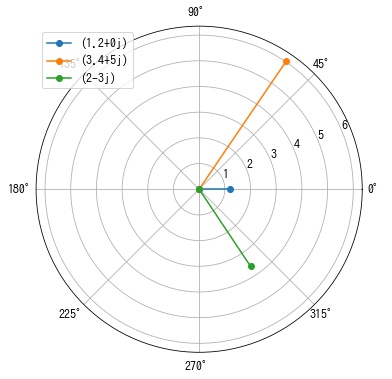
In [5]:
import numpy as np
from matplotlib import pyplot as plt
arr = np.array([1.2, 3.4 + 5j, 2 - 3j])
print("angle (radian)", np.angle(arr))
print("angle (degree)", np.angle(arr, deg=True))
fig = plt.figure(figsize=(6, 6))
ax = fig.add_subplot(111, projection="polar")
ax.grid(True)
for x in arr:
ax.plot([0, np.angle(x)], [0, np.abs(x)], label=x, marker="o")
ax.legend()
plt.show()angle (radian) [ 0. 0.97361967 -0.98279372] angle (degree) [ 0. 55.78429787 -56.30993247]
numpy.isreal
要素ごとに実数かどうか判定し、bool 配列を返します。
numpy.isreal(x)
引数
| 名前 | 型 | デフォルト値 |
|---|---|---|
| x | array_like | |
| 入力配列。 | ||
返り値
| 名前 | 説明 |
|---|---|
| out | 出力配列。 |
In [6]:
a = np.array([1.2, 3.4 + 5j, 6j])
print(np.isreal(a))[ True False False]
numpy.iscomplex
要素ごとに複素数かどうか判定し、bool 配列を返します。
numpy.iscomplex(x)
引数
| 名前 | 型 | デフォルト値 |
|---|---|---|
| x | array_like | |
| 入力配列。 | ||
返り値
| 名前 | 説明 |
|---|---|
| out | 出力配列。 |
In [7]:
a = np.array([1.2, 3.4 + 5j, 6j])
print(np.iscomplex(a))[False True True]
numpy.iscomplexobj
複素数型である、または配列に複素数が1つでも含まれる場合は True を返します。
numpy.iscomplexobj(x)
引数
| 名前 | 型 | デフォルト値 |
|---|---|---|
| x | any | |
| 入力配列。 | ||
返り値
| 名前 | 説明 |
|---|---|
| iscomplexobj | x が複素数型である、または配列に複素数が1つでも含まれる場合は True を返します。 |
In [8]:
print(np.iscomplexobj([1.2, 3.4 + 5j, 6j]))
print(np.iscomplexobj([1.2, 3.4, 6]))
print(np.iscomplexobj(np.array([1.2, 3.4, 6], dtype=np.complex64)))True False True
numpy.isrealobj
複素数型でない、または配列に複素数が1つも含まれない場合は True を返します。
numpy.isrealobj(x)
引数
| 名前 | 型 | デフォルト値 |
|---|---|---|
| x | any | |
| 入力配列。 | ||
返り値
| 名前 | 説明 |
|---|---|
| y | x が複素数型でない、または配列に複素数が1つも含まれない場合は True を返します。 |
In [9]:
print(np.isrealobj([1.2, 3.4 + 5j, 6j]))
print(np.isrealobj([1.2, 3.4, 6]))
print(np.isrealobj(np.array([1.2, 3.4, 6], dtype=np.complex64)))False True False


コメント