概要
麻雀において裏ドラが乗る確率について考察します。
ドラが1枚の場合の裏ドラが乗る確率
槓ドラがないドラが1枚の場合の裏ドラが乗る確率について考えます。 場に見えていない牌の枚数が $N$ 枚、手牌の $i, (i = 1, 2, 3, 4)$ 枚の牌のドラ表示牌の残り枚数の合計を $h_i$ としたとき、
- 裏ドラが乗らない確率: $\frac{N – \sum_{i = 1}^4 h_i}{N}$
- 裏ドラが1枚乗る確率: $\frac{h_1}{N}$
- 裏ドラが2枚乗る確率: $\frac{h_2}{N}$
- 裏ドラが3枚乗る確率: $\frac{h_3}{N}$
- 裏ドラが4枚乗る確率: $\frac{h_4}{N}$
で計算できます。次の和了形で具体的に計算してみましょう。

今回はこれ以外の牌はまだ場に見えていないものと仮定すると、各牌の残り枚数は以下の表になります。実際は自分の手牌、河及び他プレイヤーの河、副露している牌を除いたものが場に見えていない牌になります。
| 1萬 | 2萬 | 3萬 | 4萬 | 5萬 | 6萬 | 7萬 | 8萬 | 9萬 |
| 4枚 | 1枚 | 4枚 | 4枚 | 3枚 | 3枚 | 3枚 | 4枚 | 4枚 |
| 1筒 | 2筒 | 3筒 | 4筒 | 5筒 | 6筒 | 7筒 | 8筒 | 9筒 |
| 4枚 | 4枚 | 3枚 | 3枚 | 3枚 | 4枚 | 4枚 | 4枚 | 4枚 |
| 1索 | 2索 | 3索 | 4索 | 5索 | 6索 | 7索 | 8索 | 9索 |
| 4枚 | 4枚 | 2枚 | 4枚 | 3枚 | 3枚 | 3枚 | 4枚 | 4枚 |
| 東 | 南 | 西 | 北 | 白 | 発 | 中 | ||
| 4枚 | 4枚 | 4枚 | 4枚 | 4枚 | 4枚 | 4枚 |
手牌の牌の種類を枚数別に分類し、その牌が裏ドラとなるドラ表示牌の残り枚数を数えます。
| 牌の枚数 | 牌 | ドラ表示牌 | ドラ表示牌の残り枚数 |
|---|---|---|---|
| 1枚 | 567m345p567s | 456m234p456s | 4 + 3 + 3 + 4 + 3 + 3 + 4 + 3 + 3 = 30 |
| 2枚 | 3s | 2s | 4 |
| 3枚 | 2m | 1m | 4 |
| 4枚 |
よって、この手牌の裏ドラの乗る確率は $N = 136 – 14 = 122, h_1 = 30, h_2 = 4, h_3 = 4, h_4 = 0$ より、以下のように計算できます。
- 裏ドラが乗らない確率: $\frac{122 – (30 + 4 + 4)}{122} = 0.69$
- 裏ドラが1枚乗る確率: $\frac{30}{122} = 0.25$
- 裏ドラが2枚乗る確率: $\frac{4}{122} = 0.03$
- 裏ドラが3枚乗る確率: $\frac{4}{122} = 0.03$
- 裏ドラが4枚乗る確率: $\frac{0}{122} = 0$
平和形の手牌で31%の確率で裏ドラが乗るという結果になりました。実際は和了の時点では残り枚数は122枚より少なくなっているので、もう少し確率は高くなり、およそ3回に1回は裏が乗ります。
槓ドラがある場合の裏ドラが乗る確率
次に槓ドラがある場合の裏ドラが乗る確率を考えます。 厳密に計算するのは大変そうなので、シミュレーションで求めることにします。 設定は簡単で、123567m123567p33s という平和形で手牌以外の牌からドラの枚数分ランダムに裏ドラ表示牌を選択して、乗った裏ドラの枚数を数えるという試行を1000万回行い集計します。 その結果、以下のようになりました。
| 裏ドラの枚数 | 0枚 | 1枚 | 2枚 | 3枚 | 4枚 | 5枚 | 6枚 | 7枚 | 8枚 | 1枚以上 |
|---|---|---|---|---|---|---|---|---|---|---|
| 表ドラの枚数 | ||||||||||
| 1枚 | 63.95% | 32.78% | 3.27% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 36.05% |
| 2枚 | 40.67% | 42.28% | 14.80% | 2.17% | 0.08% | 0.00% | 0.00% | 0.00% | 0.00% | 59.33% |
| 3枚 | 25.75% | 40.68% | 24.69% | 7.58% | 1.22% | 0.08% | 0.00% | 0.00% | 0.00% | 74.25% |
| 4枚 | 16.22% | 34.65% | 30.15% | 14.24% | 4.01% | 0.66% | 0.06% | 0.00% | 0.00% | 83.78% |
| 5枚 | 10.18% | 27.53% | 31.37% | 20.19% | 8.18% | 2.15% | 0.36% | 0.04% | 0.00% | 89.82% |
検証に使用したコード: mahjong-cpp/create_uradora_table.cpp
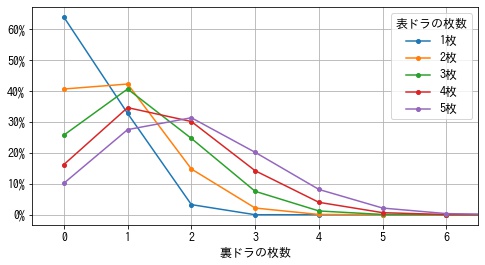
表ドラが2枚 (槓1回) の場合は1枚以上裏ドラが乗る確率は60%、3枚 (槓2回) の場合は75%とかなり高い確率で裏ドラが期待できることがわかりました。
何切るで裏ドラを考慮したほうがよいか
何切る問題を考える際に裏ドラが乗る確率まで考慮して打牌したほうがいいかどうかを次の手牌で考えます。

手牌以外に場には白や発は見えていないものとします。 ここから白または発どちらを切ってもよいように思えますが、発のドラ表示牌である白は1枚見えているため残り3枚、一方、白のドラ表示牌である中は4枚残っているため、若干白のほうが裏ドラが乗る確率が高くなります。
では、その差がどの程度なのかを麻雀何切るシミュレーター で計算してみます。すると、以下のようになりました。
## 場況
場風牌: 東, 自風牌: 東, 1巡目, 手牌の種類: 一般手, ドラ: [南]
手牌: 123m999p789s北北北白発 (0向聴)
## 計算結果
打: 発, 受け入れ枚数: 1種3枚, 有効牌: [白]
期待値: 5032点, 和了確率: 39.85%, 聴牌確率: 100.00%
打: 白, 受け入れ枚数: 1種3枚, 有効牌: [発]
期待値: 5017点, 和了確率: 39.85%, 聴牌確率: 100.00%発、白どちらを切っても和了確率は39.85%ですが、裏ドラが乗る確率が発のほうが高い分、期待値が15点高くなっています。期待値計算において、この15点というのはほぼ差がないと言えるレベルなので、裏ドラを気にするよりも、他家に対する危険度や他家からの出やすさなどの基準を優先して打牌したほうがよいと言えます。


コメント