概要
Python の数値計算ライブラリ NumPy を使って、フラクタルであるマンデルブロ集合 (Mandelbrot set) を作成し、画像で可視化する方法を解説します。
マンデルブロ集合
$$ \begin{cases} z_0(c) = 0 \\ z_{n + 1}\ (c) = (z_n(c))^2 + c \end{cases} $$で定義される複素数列 $\{z_n(c)\}$ が $n \to \infty$ で無限大に発散しない条件を満たす複素数 $c \in \mathbb{C}$ 全体の集合をマンデルブロ集合 (Mandelbrot set) といい、$\mathbb{M}$ で表します。
例:
- $c = 1$ のとき、数列 $\{z_n\}$ は $0, 1, 2, 5, 26, \cdots$ となり発散するので、マンデルブロ集合に含まれます。
- $c = -1$ のとき、数列 $\{z_n\}$ は $0, -1, 0, -1, 0, \cdots$ となり発散しないので、マンデルブロ集合に含まれません。
マンデルブロ集合の性質
コンピューターでは、極限 $\displaystyle \lim_{n \to \infty} z_n$ は計算できないため、発散するかどうかをどのように判定するかが問題になります。この問題に以下の定理が活用できます。
証明は以下を参照してください。
この定理により、第 $n$ 項まで計算した時点で $|z_n(c)| > 2$ となれば、$c$ はマンデルブロ集合に含まれないと判定できます。
Numpy による実装例
マンデルブロ集合を作成する
先にマンデルブロ集合を作成するコードを示します。
import numpy as np
from PIL import Image
def generate_mandelbrot(
real_range=(-2.0, 2.0),
imag_range=(-2.0, 2.0),
resolution=(400, 400),
iterations=100,
):
"""マンデルブロ集合を作成する。
Keyword Arguments:
real_range: 実軸の範囲を (下限, 上限) のタプルで指定する。
imag_range: 虚軸の範囲を (下限, 上限) のタプルで指定する。
resolution: 解像度を (実軸の解像度, 虚軸の解像度) のタプルで指定する。
max_iters: 反復回数
"""
# 複素平面上に格子状の点を作成する。
R, I = np.meshgrid(
np.linspace(*real_range, resolution[0]),
np.linspace(*imag_range, resolution[1]),
)
C = R + I * 1j
# 複素数列 z_i(c)
Z = np.zeros_like(C)
# 発散が確定するまでの反復回数 (|z_i(c)| <= 2 を満たす最大の i)
step = np.zeros(C.shape, dtype=int)
for i in range(iterations):
# 複素数列 z_i(c) を計算する。|z_i(c)| > 2 の場合、オーバーフローを防ぐために更新しない。
Z = np.where(np.abs(Z) <= 2, Z ** 2 + C, Z)
# |z_i(c)| <= 2 なら +1 する。
step += np.abs(Z) <= 2
return Z, step
# マンデルブロ集合を作成する。
real_range = (-2.0, 2.0) # 実軸の範囲
imag_range = (-2.0, 2.0) # 虚軸の範囲
resolution = (500, 500) # (実軸の解像度, 虚軸の解像度)
iterations = 300 # 反復回数
Z, step = generate_mandelbrot(real_range, imag_range, resolution, iterations)実軸、虚軸の範囲をそれぞれ real_range、imag_range で指定します。
複素平面のこの範囲に解像度 resolution で格子状の点を作成します。
real_range = (-2.0, 2.0)
imag_range = (-2.0, 2.0)
resolution = (10, 10)
R, I = np.meshgrid(
np.linspace(*real_range, resolution[0]), np.linspace(*imag_range, resolution[1]),
)
for 内では、複素数列 $z_i(c)$ を計算します。
$z_{i + 1}(c) = (z_i(c))^2 + c$ で数列を更新していきますが、$|z_i(c)| > 2$ の場合は発散することは確定しているので、更新を続けた結果、オーバーフローしてしまうのを防ぐために更新を止めます。
また、$|z_i(c)| \le 2$ を満たす最大の $i$ も計算します。 この計算には、True は1、False は0と同値であることを利用し、比較 $|z_i(c)| \le 2$ の結果である bool 値を足していきます。 この情報はマンデルブロ集合を色付きで画像化する際に利用します。
for i in range(iterations):
# 複素数列 z_i(c) を計算する。|z_i(c)| > 2 の場合、オーバーフローを防ぐために更新しない。
Z = np.where(np.abs(Z) <= 2, Z ** 2 + C, Z)
# |z_i(c)| <= 2 なら +1 する。
step += np.abs(Z) <= 2マンデルブロ集合を白黒画像で可視化する
マンデルブロ集合を白黒画像で画像化する例を示します。
$|z_i(c)| \le 2$ である複素数 $c$ は、発散していないので黒色 (0)、そうでないなら発散しているので白色 (255) で画像にします。
def simple_colorize(Z):
# マンデルブロ集合は黒、それ以外は白として2値画像を作成する。
img = np.where(np.abs(Z) <= 2, 0, 255).astype(np.uint8)
img = Image.fromarray(img)
return img
simple_colorize(Z)
マンデルブロ集合をカラー画像で可視化する
マンデルブロ集合をカラー画像で画像化する例を示します。
マンデルブロ集合に含まれる点 ($|z_i(c)| \le 2$ である点 $c$) の色は、前項と同様に黒色 $(0, 0, 0)$ にします。
発散している点も発散が確定した反復回数によって色を変えます。step / iterations で $[0, 1]$ の範囲の値にし、matplotlib のカラーマップで色に変換します。
def colorize(Z, step, iterations, cmap_name="jet"):
# 各点を発散が確定した反復回数に応じて色分けする。
cmap = plt.cm.get_cmap(cmap_name)
img = cmap(step / iterations, bytes=True)
# マンデルブロ集合に含まれる点の色は黒にする。
img[np.abs(Z) <= 2] = 0
img = Image.fromarray(img)
return img
img = colorize(Z, step, iterations)
img
cmap_name に matplotlib のカラーマップ名を指定し、カラーマップを変更すると、また違った雰囲気の画像が作成できます。

マンデルブロ集合の一部を拡大する
マンデルブロ集合の一部を拡大して描画したい場合は、real_range、imag_range の範囲を狭くします。
以下、$c = -0.75 + 0.1i$ の周辺を画像化した例になります。
タツノオトシゴのような模様があるので、sea horse valley (タツノオトシゴの谷) と呼ばれています。
# マンデルブロ集合の -0.75 + 0.1i 近辺の図
center = -0.75 + 0.1j
offset = 0.005
real_range = (center.real - offset, center.real + offset)
imag_range = (center.imag - offset, center.imag + offset)
resolution = (500, 500)
iterations = 1000
Z, step = generate_mandelbrot(real_range, imag_range, resolution, iterations)
img = colorize(Z, step, iterations)
img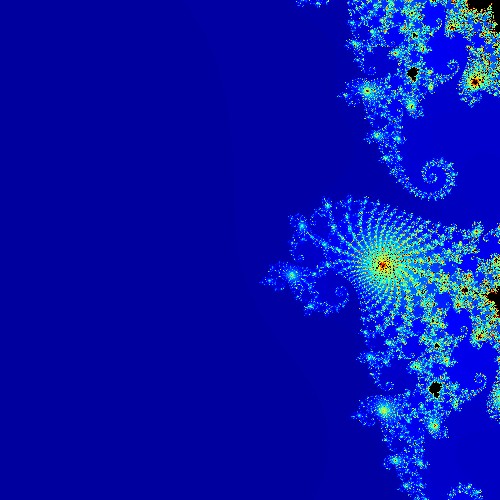


コメント