概要
バイラテラルフィルタについて解説し、OpenCV の cv2.bilateralFilter でバイラテラルフィルタを適用する方法を紹介します。
バイラテラルフィルタ
バイラテラルフィルタとは、エッジを保存しつつ、平均化を行うように設計された次で紹介するフィルタです。
ガウシアンフィルタの欠点
分散を $\sigma$、カーネルサイズを $n$ としたガウシアンフィルタの重みは以下のようになっていました。
$$ f(x, y) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left( -\frac{x^2 + y^2}{2 \sigma^2} \right) $$$$ \text{dst}(x, y) = \sum_{i = 0}^{n – 1} \sum_{j = 0}^{n – 1} f(x + i, y + j) \text{src}(x + i, y + j) $$ガウシアンフィルタは対象の画素値をより強調するように平均化を行うフィルタですが、以下の画像のようにエッジも平均化されてしまうため、物体の輪郭がぼやけた画像になります。
画像のエッジとは輝度値が大きく変わる部分です。
ガウシアンフィルタでエッジがぼやけてしまう原因は対象画素と輝度値の差が大きい画素まで考慮してしまうためです。
バイラテラルフィルタの変更点
対象画素と輝度値の差が大きい画素は小さい重み付けになるようにガウシアンフィルタの重みを以下のように変更します。
$$ f(x, y, x’, y’) = \exp \left( -\frac{x’^2 + y’^2}{2 \sigma^2} \right) \exp \left( -\frac{((\text{src}(x, y) – \text{src}(x’, y’))^2}{2 \sigma^2} \right) $$新たに追加された項の $(\text{src}(x, y) – \text{src}(x’, y’))^2$ は対象の画素値 $\text{src}(x, y)$ と周辺の画素値 $\text{src}(x’, y’)$ との距離の2乗です。これを $d$ としたとき、
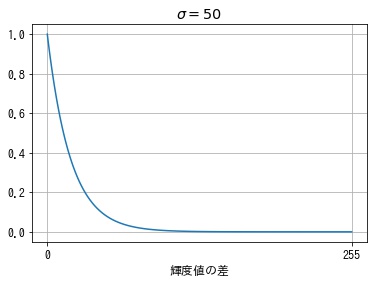
$\exp \left( -\frac{d^2}{2 \sigma^2} \right)$ のグラフを描画すると以下のようになります。 距離 $d = 0$ のとき $1$ をとり、差が大きくなるにつれ、指数関数的に $0$ に近づいていきます。この仕組みにより対象画素と輝度値の差が大きい画素について、小さな重みがつくようになります。
上の重み関数 $f(x, y, x’, y’)$ を使って、出力値は次のように計算されます。
$$ \text{dst}(x, y) = \frac{1}{c} \sum_{i = 0}^{n – 1} \sum_{j = 0}^{n – 1} f(x, y, x + i, y + j) \text{src}(x + i, y + j) $$ただし、$c$ は $\frac{1}{c} \sum_{i = 0}^{n – 1} \sum_{j = 0}^{n – 1} f(x, y, x + i, y + j) = 1$ とするための正則化項で
$$ c = \sum_{j = 0}^{n – 1} f(x, y, x + i, y + j) $$cv2.bilateralFilter
cv2.bilateralFilter() でバイラテラルフィルタを適用できます。
引数の sigmaColor、sigmaSpace は以下に対応します。
import cv2
import numpy as np
from IPython.display import Image, display
def imshow(img):
"""ndarray 配列をインラインで Notebook 上に表示する。
"""
ret, encoded = cv2.imencode(".jpg", img)
display(Image(encoded))
# 画像を読み込む。
img = cv2.imread("sample.jpg")
# バイラテラルフィルタ
dst = cv2.bilateralFilter(img, 15, sigmaColor=50, sigmaSpace=20)
imshow(dst)エッジは保持したまま、平均化ができていることが確認できます。



コメント