概要
cv2.matchShape() で 2 つの輪郭の類似度を算出し、マッチングを行う方法について解説します。
cv2.matchShape
retval = cv2.matchShapes(contour1, contour2, method, parameter)| 名前 | 型 | デフォルト値 |
|---|---|---|
| contour1 | ndarray | |
| 比較する輪郭 | ||
| contour2 | ndarray | |
| 比較する輪郭 | ||
| method | int (ShapeMatchModes) | |
| 比較方法 | ||
| parameter | float | |
| 比較方法に関するパラメータ (現在は使用されていない) | ||
| 名前 | 説明 | ||
|---|---|---|---|
| retval | 類似度 | ||
サンプルコード
import cv2
# 画像を読み込む。
img = cv2.imread("sample.jpg")
# グレースケールに変換する。
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# 2値化する。
binary = cv2.threshold(gray, 100, 255, cv2.THRESH_BINARY)[1]
# 輪郭を抽出する。
contours, hierarchy = cv2.findContours(
binary, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE
)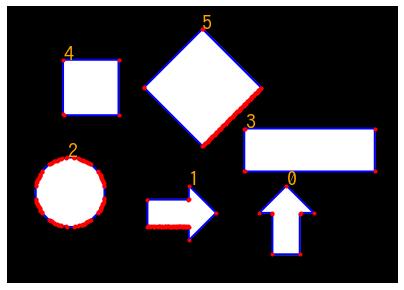
サンプル画像の図形には以下の特徴があります。
- No0 と No1 は形状と大きさが同じですが、角度が異なります。
- No4 と No5 は形状が同じですが、大きさと角度が異なります。
cv2.matchShapes() は、2 つの輪郭を渡すとその類似度を返します。類似度は小さいほど、形状がより似ていることを意味します。各輪郭同士の類似度を計算し、$M_{ij}$ を輪郭 $i$ と輪郭 $j$ の類似度を表す行列としてまとめてみます。
import cv2
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
num_cnts = len(contours)
# 類似度を計算する。
matches = np.empty((num_cnts, num_cnts))
for i, j in np.ndindex(*matches.shape):
matches[i, j] = cv2.matchShapes(contours[i], contours[j], cv2.CONTOURS_MATCH_I1, 0)
# 行列を可視化する。
fig, ax = plt.subplots(figsize=(7, 7))
ax = sns.heatmap(
matches, annot=True, cmap="Reds", ax=ax, fmt=".2f", annot_kws={"size": 16}
)
plt.show()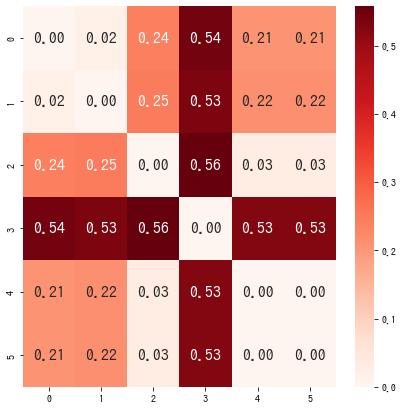
対角成分 $M_{ii}$ は同じ輪郭同士の比較なので、類似度は 0 になります。2 つの輪郭が近いほど類似度は 0 に近くなるため、ある閾値を設定し、その値未満の類似度を持つ輪郭同士を同一であると判定することができます。
threshold = 0.02
tril_indices = np.triu_indices(len(matches), k=1)
for i, j in zip(*tril_indices):
if matches[i, j] < threshold:
print(f"輪郭{i} vs 輪郭{j}: 類似度: {matches[i, j]:.2f}")輪郭0 vs 輪郭1: 類似度: 0.02 輪郭4 vs 輪郭5: 類似度: 0.00
その結果、No0 と No1、No4 と No5 が同じ輪郭であると判定されました。
比較方法 – method
輪郭の類似度を算出する際、スケール、位置、回転に不変な 7 つの要素で表される HuMoments を各輪郭に対して計算し、その HuMoments の距離を算出します。この距離の計算方法は method 引数で指定できます。
2 つの輪郭 $A, B$ が与えられたとき、それぞれの HuMoments を $h_i^A, h_i^B, (i = 1, 2, \cdots, 7)$ とします。
HuMoments の値に対して、以下のように定義された距離指標が使用されます。
cv2.CONTOURS_MATCH_I1
$$ I_1(A,B) = \sum_{i = 1}^7 \left| \frac{1}{m^A_i} – \frac{1}{m^B_i} \right| $$
cv2.CONTOURS_MATCH_I2
$$ I_2(A,B) = \sum_{i = 1}^7 \left| m^A_i – m^B_i \right| $$
cv.CONTOURS_MATCH_I3 $$ I_3(A,B) = \max_i \frac{ \left| m^A_i – m^B_i \right| }{ \left| m^A_i \right| } $$
ここで、$m_i^A = \text{sign}(h_i^A) \log h_i^A, m_i^B = \text{sign}(h_i^B) \log h_i^B$ です。


コメント