目次
概要
平均化フィルタとガウシアンフィルタについて解説し、OpenCV での適用方法について紹介します。
平均化フィルタ
平均化フィルタ (averaging filter) は、カーネル内の画素の平均を計算するフィルタです。
$$ \text{dst}(x, y) = \frac{1}{N^2} \sum_{i = 1}^N \sum_{j = 1}^N \text{src}(x + i, y + j) $$フィルタのサイズが $N \times N$ の場合、各フィルタの値を $f(i, j) = \frac{1}{N^2}$ とすることで実現できます。
(3, 3) の平均化フィルタ
| $\frac{1}{9}$ | $\frac{1}{9}$ | $\frac{1}{9}$ |
| $\frac{1}{9}$ | $\frac{1}{9}$ | $\frac{1}{9}$ |
| $\frac{1}{9}$ | $\frac{1}{9}$ | $\frac{1}{9}$ |
平均化フィルタは画像のエッジを滑らかにします。
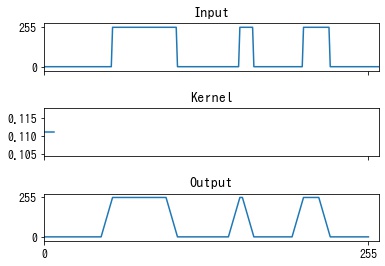
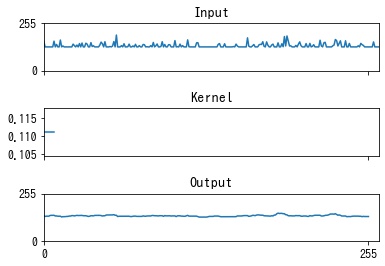
エッジが滑らかになることで、ノイズが軽減します。
cv2.blur
cv2.blur() で平均化フィルタを適用できます。
In [1]:
import cv2
import numpy as np
from IPython.display import Image, display
def imshow(img):
"""ndarray 配列をインラインで Notebook 上に表示する。
"""
ret, encoded = cv2.imencode(".jpg", img)
display(Image(encoded))
# 画像を読み込む。
img = cv2.imread("sample.jpg")
# フィルタリングを行う。
dst = cv2.blur(img, (3, 3))
imshow(dst)
エッジが滑らかになることで、画像全体がぼやけた感じになります。
ガウシアンフィルタ
ガウシアンフィルタ (Gaussian filter) は、ガウス分布 (正規分布)で重み付けしたカーネルを使用するフィルタです。ガウス分布は以下のような単峰型の分布です。
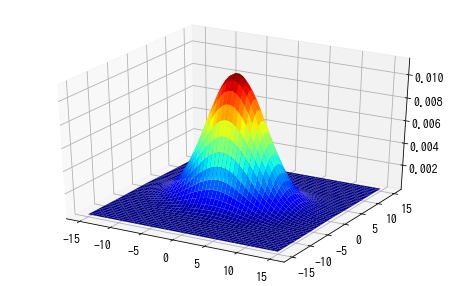
ガウシアンフィルタは以下のように導出できます。
多次元正規分布の確率密度関数
$$ f(\bm{x}) = \dfrac{1}{(2\pi)^{\frac{n}{2}}\sqrt{|\Sigma|}} \exp \left\{ -\dfrac{1}{2}(\bm{x} – \bm{\mu})^T \Sigma^{-1} (\bm{x} – \bm{\mu})\right\} $$について、
$ \Sigma = \begin{pmatrix} \sigma_x & 0 \\ 0 & \sigma_y \\ \end{pmatrix} $, $n = 2$, $\bm{x} = (x, y)^T$, $\bm{\mu} = \bm{0}$ とおくと、
$$ f(x, y) = \frac{1}{\sqrt{2 \pi \sigma_x \sigma_y}} \exp \left( -\frac{1}{2} \left(\frac{x^2}{\sigma_x} + \frac{y^2}{\sigma_y} \right) \right) $$$\sigma_x = \sigma_y = \sigma$ の場合は
$$ f(x, y) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left( -\frac{x^2 + y^2}{2 \sigma^2} \right) $$ガウシアンフィルタは画像のエッジを滑らかにします。
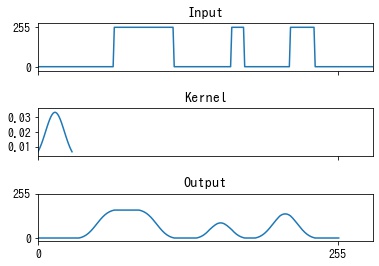
エッジが滑らかになることで、ノイズが軽減します。
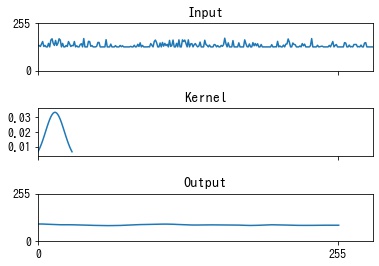
cv2.GaussianBlur
cv2.GaussianBlur() でガウシアンフィルタを適用できます。
dst = cv2.GaussianBlur(src, ksize, sigmaX[, dst[, sigmaY[, borderType]]])simgaX のみ指定した場合は、sigmaX = sigmaY となります。
In [2]:
dst = cv2.GaussianBlur(img, (5, 5), sigmaX=1)
imshow(dst)



コメント