概要
OpenCV でテンプレートマッチングを行う方法について解説します。
テンプレートマッチング
検出対象の物体が映るテンプレート画像を用意します。
入力画像に対して、テンプレート画像と同じ大きさの検索窓を左上から右下にかけてスライドさせながら移動させます。 移動する検索窓の各位置において、「入力画像の検索窓の範囲」と「テンプレート画像」の類似度を計算します。 検索窓のすべての位置で計算された類似度が最終的な出力結果になります。
cv2.matchTemplate
result = cv2.matchTemplate(image, templ, method[, result[, mask]])公式リファレンス: cv2.matchTemplate
| 名前 | 型 | デフォルト値 |
|---|---|---|
| image | ndarray | |
| 入力画像 | ||
| templ | ndarray | |
| テンプレート画像 | ||
| method | TemplateMatchModes | |
| 類似度の計算方法 | ||
| 名前 | 説明 | ||
|---|---|---|---|
| result | 検索窓の各位置での類似度 | ||
サンプルコード
入力画像からテンプレート画像の ❓ ボックスを探します。
入力画像
テンプレート画像
import cv2
import numpy as np
from IPython.display import Image, display
from matplotlib import pyplot as plt
def imshow(img):
"""ndarray 配列をインラインで Notebook 上に表示する。"""
ret, encoded = cv2.imencode(".jpg", img)
display(Image(encoded))# 入力画像、テンプレート画像を読み込む。
img = cv2.imread("sample1.jpg") # 入力画像
templ = cv2.imread("template.jpg") # テンプレート画像
# テンプレートマッチングを行う。
result = cv2.matchTemplate(img, templ, cv2.TM_CCOEFF_NORMED)result について
返り値 result は、検索窓の各位置でのテンプレート画像との類似度を表す 2 次元配列です。
入力画像の大きさを $(W, H)$、テンプレート画像の大きさを $(w, h)$、検索窓の左上の点を $(x, y)$ としたとき、
検索窓は $(x, y) \in (W − w + 1, H − h + 1)$ の範囲でスライドします。
result[y, x] は検索窓が位置 (x, y) から $(x + w, y + h)$ にあるときの類似度の値になります。
print("img.shape", img.shape) # (380, 694, 3)
print("template.shape", templ.shape) # (30, 31, 3)
print("result.shape", result.shape) # (380 - 30 + 1, 694 - 31 + 1) = (351, 664)img.shape (380, 694, 3) template.shape (29, 33, 3) result.shape (352, 662)
matplotlib で類似度のヒートマップを描画します。黄色のところは類似度が高いことを意味します。
fig, ax = plt.subplots(figsize=(10, 5))
im = ax.imshow(result, cmap="jet")
fig.colorbar(im)
plt.show()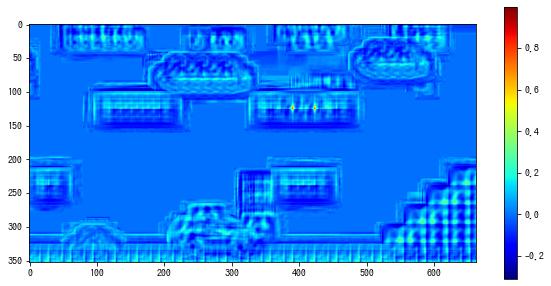
類似度が最も高い場所を探す
テンプレート画像が最もマッチする位置を探すには、cv2.minMaxLoc() を使用します。
この関数は、配列の最大値、最小値およびそれぞれの位置を返します。
# 最も類似度が高い位置を取得する。
minVal, maxVal, minLoc, maxLoc = cv2.minMaxLoc(result)
print(f"max value: {maxVal}, position: {maxLoc}")
# max value: 0.9999998211860657, position: (392, 124)
# 描画する。
tl = maxLoc[0], maxLoc[1]
br = maxLoc[0] + templ.shape[1], maxLoc[1] + templ.shape[0]
dst = img.copy()
cv2.rectangle(dst, tl, br, color=(0, 255, 0), thickness=2)
imshow(dst)max value: 0.997153639793396, position: (390, 124)

類似度が閾値以上の場所を探す
類似度が最も高い場所を探した場合、2 つある ❓ ブロックのうち 1 つしか検出されません。 類似度が一定以上の場所はすべて検出するように変更するには、以下のようにします。
# 最も類似度が 0.9 以上の位置を取得する。
ys, xs = np.where(result >= 0.9)
# 描画する。
dst = img.copy()
for x, y in zip(xs, ys):
cv2.rectangle(
dst,
(x, y),
(x + templ.shape[1], y + templ.shape[0]),
color=(0, 255, 0),
thickness=2,
)
imshow(dst)
類似度の計算方法
method 引数で指定できる類似度の計算方法には以下があります。とくに拘りがなければ、cv2.CCOEFF_NORMED にしておくとよいでしょう。
入力画像を $I$、テンプレート画像を $T$、出力結果を $\text{result}$ とします。 検索窓が位置 $(x, y)$ にあり、入力画像の検索窓の領域およびテンプレート画像の画素を 1 次元配列としたものを $\bm{u}_{xy}, \bm{v}_{xy}$ としたとき、類似度の計算はこの 2 つのベクトルの類似度を計算することに他なりません。
cv2.TM_SQDIFF
類似度を二乗差 (sum of square difference, SQDIFF) で計算します。
$$ \begin{aligned} \text{result}(x, y) &= \sum_{i, j} {(T(i, j) – I(x + i, y + j))^2} \\ &= \|\bm{u}_{xy} – \bm{v}_{xy}\|^2 \end{aligned} $$cv2.TM_SQDIFF_NORMED
類似度を正規化二乗差 (normalized square difference) で計算します。
$$ \begin{aligned} \text{result}(x, y) &= \frac {\sum_{i, j} (T(i, j) – I(x + i, y + j))^2} {\sqrt{\sum_{i, j} T(i, j)^2} \sqrt{\sum_{i, j} I(x + i, y + j)^2}} \\ &= \frac{\|\bm{u}_{xy} – \bm{v}_{xy}\|^2}{\|\bm{u}_{xy}\| \|\bm{v}_{xy}\|} \end{aligned} $$cv2.TM_CCORR
類似度を相互相関 (cross correlation, CCORR) で計算します。
$$ \begin{aligned} \text{result}(x, y) &= \sum_{i, j} T(i, j) I(x + i, y + j) \\ &= \bm{u}_{xy} \cdot \bm{v}_{xy} \end{aligned} $$cv2.TM_CCORR_NORMED
類似度を正規化相互相関 (normalized cross correlation) で計算します。 これはベクトル $\bm{u}_{xy}, \bm{v}_{xy}$ のなす角を $\theta$ としたときの $\cos \theta$ であり、コサイン類似度と呼ばれます。 出力値は $[-1, 1]$ の範囲になります。
$$ \begin{aligned} \text{result}(x, y) &= \frac{\sum_{i, j} T(i, j) I(x + i,y + j)} {\sqrt{\sum_{i, j} T(i, j)^2} \sqrt{\sum_{i, j} I(x + i, y + j)^2}}] \\ &= \frac{\bm{u}_{xy} \cdot \bm{v}_{xy}}{\|\bm{u}_{xy}\| \|\bm{v}_{xy}\|} \end{aligned} $$cv2.TM_CCOEFF
類似度を相関係数 (correlation coefficient, COOEFF) で計算します。
$$ \begin{aligned} \text{result}(x, y) &= \sum_{i, j} (T'(i, j) \cdot I'(x + i, y + j)) \\ &= (\bm{u}_{xy} – \bar{\bm{u}}_{xy}) \cdot (\bm{v}_{xy} – \bar{\bm{v}}_{xy}) \end{aligned} $$ただし、
$$ \begin{aligned} T'(i, j) &= T(i, j) – \frac{1}{wh} \sum_{i’, j’} T(i’, j’) \\ I'(x + i, y + j) &= I(x + i, y + j) – \frac{1}{wh} \sum_{i’, j’} I(x + i’, y + j’) \end{aligned} $$cv2.TM_CCOEFF_NORMED
類似度を正規化相関係数 (normalized correlation coefficient) で計算します。 出力値は $[-1, 1]$ の範囲になります。
$$ \begin{aligned} result(x, y) &= \frac {\sum_{i, j} (T'(i, j) \cdot I'(x + i, y + j))} {\sqrt{\sum_{i, j} T'(i, j)^2 \cdot \sum_{i, j} I'(x + i, y + j)^2}} \\ &= \frac{(\bm{u}_{xy} – \bar{\bm{u}}_{xy}) \cdot (\bm{v}_{xy} – \bar{\bm{v}}_{xy})} {\|\bm{u}_{xy} – \bar{\bm{u}}_{xy}\| \|\bm{v}_{xy} – \bar{\bm{v}}_{xy}\|} \end{aligned} $$各 method のよる結果の違い
params = [
"TM_SQDIFF",
"TM_SQDIFF_NORMED",
"TM_CCORR",
"TM_CCORR_NORMED",
"TM_CCOEFF",
"TM_CCOEFF_NORMED",
]
fig = plt.figure(figsize=(10, 10))
for i, param in enumerate(params, 1):
result = cv2.matchTemplate(img, templ, getattr(cv2, param))
ax = fig.add_subplot(3, 2, i)
ax.set_title(param)
ax.imshow(result, cmap="jet")
plt.show()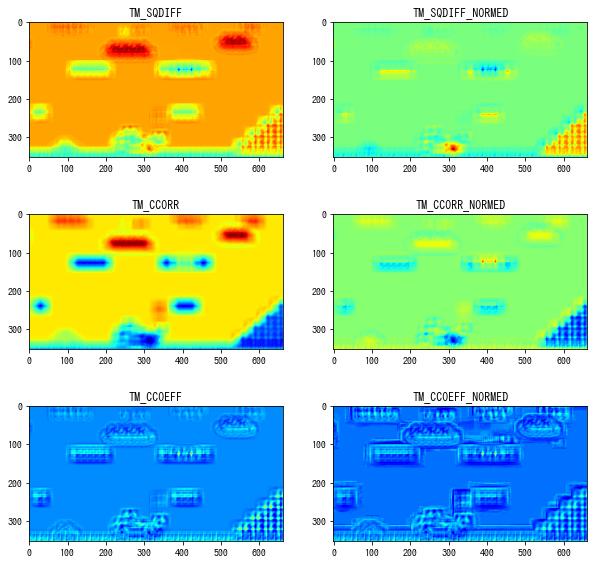




コメント