OpenCV – watershed セグメンテーションの仕組み

概要

画像の各画素をインスタンスごとにラベル付けするセグメンテーションタスクで使用される watershed アルゴリズムを解説します。

watershed アルゴリズムの概要

下記のグレースケール画像をセグメンテーションすることを考えます。

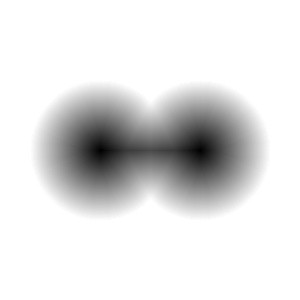
グレースケール画像を位置 $(x, y)$ が画素値 $I(x, y)$ に対応する関数と考えて可視化すると、下記のような形状になります。

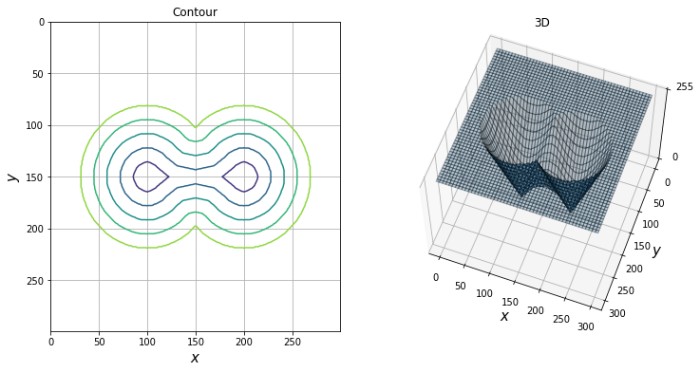
$I(x, y) \ne 255$ である傾斜 (relief) がある領域 $R$ をセグメンテーション (下図の緑の枠の内側) することを考えます。

Watershed

マーカー基準の watershed アルゴリズム

Relief の領域に対して、背景ラベルとセグメンテーションのシードとなるラベルを予め用意します。

Watershed

$R$: 傾斜の領域。各要素 $(i, r_i) \in R$ は、位置 $i$ 及びその位置の画素値 $r_i$ を表します。
$M$: 傾斜の領域に対応するマーカー。各要素 $(i, m_i) \in M$ は、位置 $i$ 及びその位置のラベル $m_i$ を表します。ラベルが未確定の領域 (灰色) は、背景 $m_i = BG$ を設定します。

入力として、$R, M$ が与えられたとき、watershed アルゴリズムでは、次のようにセグメンテーションを行います。

位置 $i$ に隣接する $M$ の要素の集合を $N_D(i, m_i)$ とします。このとき、傾斜の領域で背景でない各要素 $(i, r_i) \in R, m_i \ne BG$ について、$(j, m_j) \in N_D(i, m_i), m_j \ne BG$ が存在するか調べます。存在する場合、位置 $i$ を値、画素値 $r_i$を優先度として、優先度キューに追加します。つまり、背景とそれ以外のラベルの境界の要素を優先度キューに追加します。

Watershed

キューから優先度が一番高い要素、つまり、画素値 $r_i$ が一番小さい要素を取り出します。キューが空の場合はアルゴリズムを終了します。
キューから取り出された位置が $i$ であるとき、$(j, m_j) \in N_D(i, m_i), m_j = BG$ が存在するか調べます。存在する場合、そのラベルを位置 $i$ のラベル $m_i$ に変更します。
ラベルの変更が行われた要素は、値を $j$、優先度を $max(r_i, r_j)$ として優先度キューに追加します。その後、2 に戻ります。

上記の仕組みは簡単にいうと、背景との境界の要素を起点として、背景以外のラベルを隣へと広げています。広げる際は、画素値が小さい要素から順番に広げていきますが、この画素値が小さい要素を探す作業を効率的に行うために、優先度キューを使用しています。背景の要素が無くなったらアルゴリズムが終了します。

以下に Python による実装を示します。

In [1]:

import cv2
from IPython.display import Image, display


def imshow(img):
    """ndarray 配列をインラインで Notebook 上に表示する。"""
    ret, encoded = cv2.imencode(".jpg", img)
    display(Image(encoded))

マーカーを以下の手順で作成します。

ネガポジ反転
2 値化
ラベリング

マーカー作成

以上により、背景(値=0)、ラベル赤(値=1)、ラベル青(値=2) の 3 種類のラベルを持つマーカーが作成できました。

In [2]:

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 画像を読み込む。
I = cv2.imread("sample1.png", cv2.IMREAD_GRAYSCALE)
imshow(I)

# マーカーを作成する。
INV_I = 255 - I
ret, INV_I_thresh = cv2.threshold(INV_I, 0.8 * INV_I.max(), 255, cv2.THRESH_BINARY)
ret, init_M = cv2.connectedComponents(INV_I_thresh)

# マーカーを可視化する。
fig, ax = plt.subplots(figsize=(6, 6))
ax.imshow(init_M, cmap="tab20b")
ax.set_xlabel("$x$", fontsize=15)
ax.set_ylabel("$y$", fontsize=15)
plt.show()

傾斜 (Relief) の領域の位置の一覧、その各位置ごとに隣接する位置の一覧を予め作成しておきます。

In [3]:

BG = 0  # 背景ラベル
h, w = I.shape  # 画像の幅、高さ

# Relief の位置の一覧を作成する。
indices = [tuple(i) for i in np.mgrid[:h, :w].reshape(2, -1).T]
R = [i for i in indices if I[i] != 255]


def get_neighbors(h, w, i, I):
    i1_min = max(0, i[0] - 1)
    i1_max = min(h, i[0] + 2)
    i2_min = max(0, i[1] - 1)
    i2_max = min(w, i[1] + 2)
    indices = [
        tuple(j) for j in np.mgrid[i1_min:i1_max, i2_min:i2_max].reshape(2, -1).T
    ]
    N = [j for j in indices if j != i and I[j] != 255]

    return N


# Relief の各位置について、Relief の隣接する位置の一覧を作成する。
N = {
    i: get_neighbors(h, w, i, I) for i in R
}  # N[i] = 位置 i に隣接する要素の位置の一覧

Relief の要素について、周囲の要素に背景ラベルが存在する場合、その要素を優先度キューに追加します。

In [4]:

import heapq

queue = []  # 優先度キュー
M = init_M.copy()  # マーカー

for i in R:
    if M[i] == BG:
        continue

    if any(M[j] == BG for j in N[i]):
        # 周囲の要素に背景ラベルが存在する場合、その要素を優先度キューに追加する。
        heapq.heappush(queue, (I[i], i))

Python の優先度キューは pop すると、優先度が最小の要素が返ります。優先度は画素値としていたので、つまり、画素値が最小の要素が取得できます。取り出した要素の周囲に背景ラベルがある場合、取り出した要素のラベルに張替え、張り替えた要素を優先度キューに追加します。優先度キューが空になった場合、処理を終了します。

In [5]:

while queue:
    # 優先度キューから画素値が最小の位置を取り出す。
    _, i = heapq.heappop(queue)

    for j in N[i]:
        if M[j] == BG:
            # 隣接する要素のラベルが背景の場合、要素 i のラベルに張り替える。
            M[j] = M[i]

            # ラベルを更新した要素を優先度キューに追加する。
            heapq.heappush(queue, (min(I[i], I[j]), j))

以下のように、$R$ の要素がすべてラベル付けされたことが確認できます。

In [6]:

# マーカーを可視化する。
fig, ax = plt.subplots(figsize=(6, 6))
ax.imshow(M, cmap="tab20b")
ax.set_xlabel("$x$", fontsize=15)
ax.set_ylabel("$y$", fontsize=15)
plt.show()