scipy – scipy.stats の使い方まとめ

概要
確率変数
1. scipy.stats.rv_discrete
2. scipy.stats.rv_continuous

概要

確率分布を扱う scipy のモジュールである scipy.stats の使い方について解説します。

確率変数

離散型及び連続型確率変数を表すクラスが提供されています。

scipy.stats.rv_discrete

scipy.stats.rv_discrete は離散型確率変数を表すクラスです。

In [1]:

import numpy as np
from matplotlib import pyplot as plt
import scipy.stats as stats

# ポアソン分布に従う確率変数を作成する。
X = stats.poisson(2)

サンプリング

scipy.stats.rv_discrete.rvs() で確率変数から観測値を取得します。

In [2]:

print(X.rvs(size=20))

[4 1 0 2 1 1 3 1 2 0 2 1 1 3 3 2 3 1 0 1]

確率質量関数

scipy.stats.rv_discrete.pmf() は、確率質量関数の値 $f_X(x)$ を返します。

In [3]:

fig, ax = plt.subplots()

x = np.arange(20)
y = X.pmf(x)

ax.stem(x, y, use_line_collection=True)
ax.grid()
ax.set_xticks(np.arange(0, 21, 2))

plt.show()

scipy.stats.rv_discrete.logpmf() は、確率質量関数の対数をとった値 $\log f_X(x)$ を返します。

In [4]:

fig, ax = plt.subplots()

x = np.arange(20)
y = X.logpmf(x)

ax.stem(x, y, use_line_collection=True)
ax.grid()
ax.set_xticks(np.arange(0, 21, 2))

plt.show()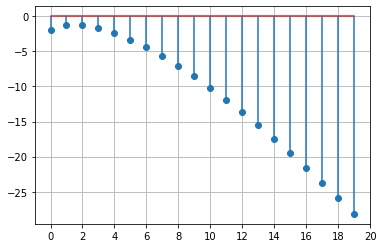

累積分布関数

scipy.stats.rv_discrete.cdf() は、累積分布関数 $F_X(x) = P(X \le x)$ の値を返します。

In [5]:

fig, ax = plt.subplots()

x = np.linspace(0, 20, 100)
y = X.cdf(x)

ax.plot(x, y)
ax.grid()
ax.set_xticks(np.arange(0, 21, 2))

plt.show()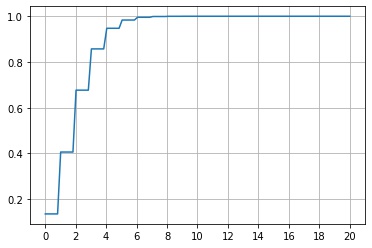

scipy.stats.rv_discrete.logcdf() は、累積分布関数の対数をとった値 $\log F_X(x)$ を返します。

In [6]:

fig, ax = plt.subplots()

x = np.linspace(0, 20, 100)
y = X.logcdf(x)

ax.plot(x, y)
ax.grid()
ax.set_xticks(np.arange(0, 21, 2))

plt.show()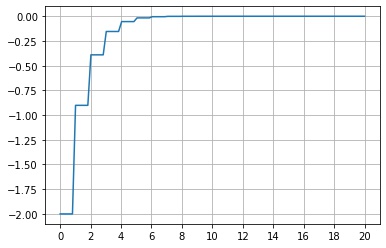

生存関数

scipy.stats.rv_discrete.sf() は、生存関数 $S_X(x) = P(X > x) = 1 – F_X(x)$ の値を返します。

In [7]:

fig, ax = plt.subplots()

x1 = np.linspace(0, 20, 100)
y1 = X.cdf(x1)

x2 = np.linspace(0, 20, 100)
y2 = X.sf(x2)

ax.plot(x1, y1, label="cdf")
ax.plot(x2, y2, label="sf")
ax.legend()
ax.grid()
ax.set_xticks(np.arange(0, 21, 2))

plt.show()

scipy.stats.rv_discrete.logsf() は、生存関数の対数をとった値 $\log S_X(x)$ を返します。

In [8]:

fig, ax = plt.subplots()

x1 = np.linspace(0, 20, 100)
y1 = X.logcdf(x1)

x2 = np.linspace(0, 20, 100)
y2 = X.logsf(x2)

ax.plot(x1, y1, label="logcdf")
ax.plot(x2, y2, label="logsf")
ax.legend()
ax.grid()
ax.set_xticks(np.arange(0, 21, 2))

plt.show()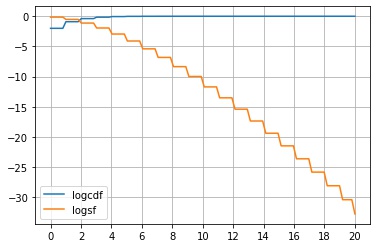

分位関数 (累積分布関数の逆関数)

scipy.stats.rv_discrete.ppf() は分位関数 $Q(p) = \inf \{ x \in \R \mid p \le F(x) \}$ の値を返します。

In [9]:

fig, ax = plt.subplots()

p = np.linspace(0, 1, 100)
x = X.ppf(p)

ax.plot(p, x)
ax.grid()

plt.show()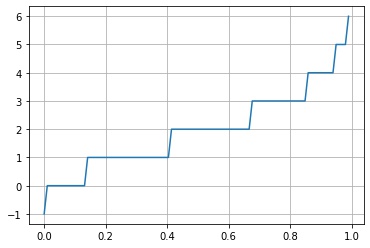

生存関数の逆関数

scipy.stats.rv_discrete.isf() は生存関数の逆関数の値 $Q(p) = \inf \{ x \in \R \mid p \le S_X(x) \}$ を返します。

In [10]:

fig, ax = plt.subplots()

p = np.linspace(0, 1, 100)
x = X.isf(p)

ax.plot(p, x)
ax.grid()

plt.show()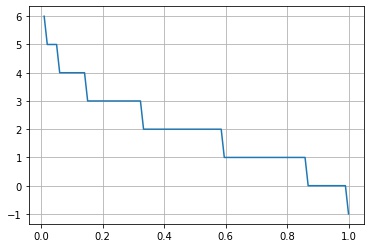

モーメント

scipy.stats.rv_discrete.moment() は $n$ 次のモーメントを計算します。

In [11]:

for i in range(1, 5):
    m = X.moment(i)
    print(fr"E[X^{i}] = {m:.2f}")

E[X^1] = 2.00
E[X^2] = 6.00
E[X^3] = 22.00
E[X^4] = 94.00

平均情報量 / エントロピー

scipy.stats.rv_discrete.entropy() で平均情報量を計算します。

In [12]:

print(X.entropy())

1.7048826439329838

統計量

scipy.stats.rv_discrete.stats() で次の統計量を計算できます。計算対象の統計量は文字列で指定します。

“m”: 期待値
“v”: 分散
“s”: 歪度 (skewness)
“k”: 尖度 (kutosis)

In [13]:

mean, var, skew, kutosis = X.stats("mvsk")
print(f"mean = {mean:.2f}")
print(f"var = {var:.2f}")
print(f"skew = {skew:.2f}")
print(f"kutosis = {kutosis:.2f}")

mean = 2.00
var = 2.00
skew = 0.71
kutosis = 0.50

In [14]:

print(f"median = {X.median():.2f}")
print(f"mean = {X.mean():.2f}")
print(f"var = {X.var():.2f}")
print(f"std = {X.std():.2f}")

median = 2.00
mean = 2.00
var = 2.00
std = 1.41

確率変数を引数にとる関数 $f$ の期待値 $E[f(X)]$ を計算する場合は scipy.stats.rv_discrete.expect() を使用します。

In [15]:

def f(x):
    return x ** 2 + 1


print(X.expect(f))

6.999999999999999

信頼区間

scipy.stats.rv_discrete.interval() は、 $\alpha$ が与えられたとき、 $P(median[X] – t \le X \le median[x] + t) = \alpha$ を満たす区間 $[median[X] – t, median[x] + t]$ を計算します。

In [16]:

a, b = X.interval(0.95)
print(f"P[{a}, {b}]")

P[0.0, 5.0]

台

scipy.stats.rv_discrete.support() は、確率質量関数の台 $\text{supp}(pmf) = \{x \in \R \mid f_X(x) > x \}$ を返します。

In [17]:

print(X.support())

(0, inf)

scipy.stats.rv_continuous

scipy.stats.rv_continuous は連続型確率変数を表すクラスです。

In [18]:

# 平均0、分散1に従う確率変数を作成する。
X = stats.norm(0, 1)

loc, scale パラメータ

すべての連続型確率変数の分布は、位置やスケールを調整するためのパラメータ loc, scale をとります。調整前の確率変数が $X$ としたとき、調整後の確率変数は以下のように計算されます。

$X’ = \frac{X – loc}{scale}$

In [19]:

fig, ax = plt.subplots()

x = np.linspace(-10, 10, 100)
y1 = stats.norm.pdf(x)
y2 = stats.norm.pdf(x, loc=2, scale=2)

ax.plot(x, y1)
ax.plot(x, y2)
ax.grid()

plt.show()

サンプリング

scipy.stats.rv_continuous.rvs() で確率変数から観測値を取得します。

In [20]:

print(X.rvs(size=20))

[ 0.52587614 -1.07375603 -1.24883296 -0.59328601  0.17404647 -0.30302527
 -1.12587053  0.47764943 -0.81734939  0.16761539 -0.09701077  1.01066471
  0.58933414  1.44496678 -0.34886864 -2.59756075  0.07253381  1.07815998
 -0.56592292  0.26258007]

確率密度関数

scipy.stats.rv_continuous.pdf() は、確率密度関数の値 $f_X(x)$ を返します。

In [21]:

fig, ax = plt.subplots()

x = np.linspace(-5, 5, 100)
y = X.pdf(x)

ax.plot(x, y)
ax.grid()

plt.show()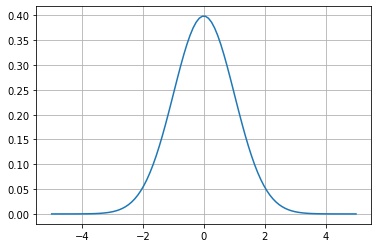

scipy.stats.rv_continuous.logpdf() は、確率密度関数の対数をとった値 $\log f_X(x)$ を返します。

In [22]:

fig, ax = plt.subplots()

x = np.linspace(-5, 5, 100)
y = X.logpdf(x)

ax.plot(x, y)
ax.grid()

plt.show()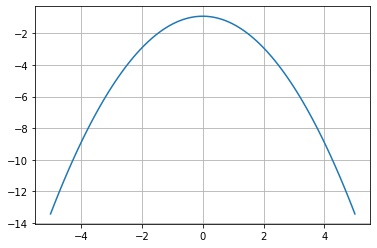

累積分布関数

scipy.stats.rv_continuous.cdf() は、累積分布関数 $F_X(x) = P(X \le x)$ の値を返します。

In [23]:

fig, ax = plt.subplots()

x = np.linspace(-5, 5, 100)
y = X.cdf(x)

ax.plot(x, y)
ax.grid()

plt.show()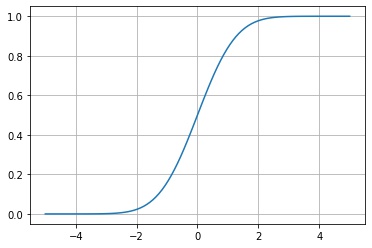

scipy.stats.rv_continuous.logcdf() は、累積分布関数の対数をとった値 $\log F_X(x)$ を返します。

In [24]:

fig, ax = plt.subplots()

x = np.linspace(-5, 5, 100)
y = X.logcdf(x)

ax.plot(x, y)
ax.grid()

plt.show()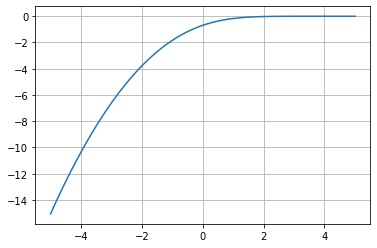

生存関数

scipy.stats.rv_continuous.sf() は、生存関数 $S_X(x) = P(X > x) = 1 – F_X(x)$ の値を返します。

In [25]:

fig, ax = plt.subplots()

x1 = np.linspace(-5, 5, 100)
y1 = X.cdf(x1)

x2 = np.linspace(-5, 5, 100)
y2 = X.sf(x2)

ax.plot(x1, y1, label="cdf")
ax.plot(x2, y2, label="sf")
ax.legend()
ax.grid()

plt.show()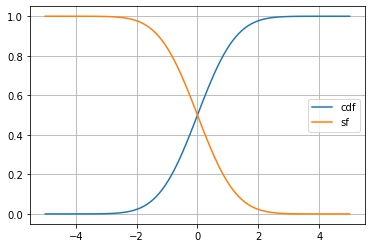

scipy.stats.rv_continuous.logsf() は、生存関数の対数をとった値 $\log S_X(x)$ を返します。

In [26]:

fig, ax = plt.subplots()

x1 = np.linspace(-5, 5, 100)
y1 = X.logcdf(x1)

x2 = np.linspace(-5, 5, 100)
y2 = X.logsf(x2)

ax.plot(x1, y1, label="logcdf")
ax.plot(x2, y2, label="logsf")
ax.legend()
ax.grid()

plt.show()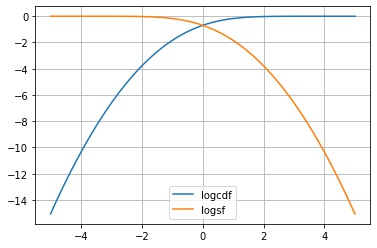

分位関数 (累積分布関数の逆関数)

scipy.stats.rv_continuous.ppf() は分位関数 $Q(p) = \inf \{ x \in \R \mid p \le F(x) \}$ の値を返します。

In [27]:

fig, ax = plt.subplots()

p = np.linspace(0, 1, 100)
x = X.ppf(p)

ax.plot(p, x)
ax.grid()

plt.show()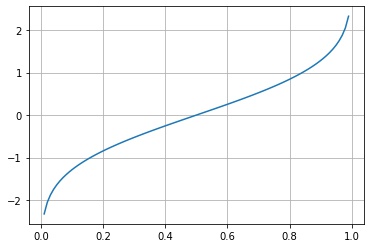

生存関数の逆関数

scipy.stats.rv_continuous.isf() は生存関数の逆関数の値 $Q(p) = \inf \{ x \in \R \mid p \le S_X(x) \}$ を返します。

In [28]:

fig, ax = plt.subplots()

p = np.linspace(0, 1, 100)
x = X.isf(p)

ax.plot(p, x)
ax.grid()

plt.show()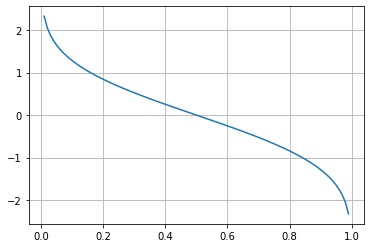

モーメント

scipy.stats.rv_continuous.moment() は $n$ 次のモーメント $E[X^n]$ を計算します。

In [29]:

for i in range(1, 5):
    m = X.moment(i)
    print(fr"E[X^{i}] = {m:.2f}")

E[X^1] = 0.00
E[X^2] = 1.00
E[X^3] = 0.00
E[X^4] = 3.00

平均情報量 / エントロピー

scipy.stats.rv_continuous.entropy() で平均情報量を計算します。

In [30]:

print(X.entropy())

1.4189385332046727

統計量

scipy.stats.rv_continuous.stats() で次の統計量を計算できます。計算対象の統計量は文字列で指定します。

“m”: 期待値
“v”: 分散
“s”: 歪度 (skewness)
“k”: 尖度 (kutosis)

In [31]:

mean, var, skew, kutosis = X.stats("mvsk")
print(f"mean = {mean:.2f}")
print(f"var = {var:.2f}")
print(f"skew = {skew:.2f}")
print(f"kutosis = {kutosis:.2f}")

mean = 0.00
var = 1.00
skew = 0.00
kutosis = 0.00

In [32]:

print(f"median = {X.median():.2f}")
print(f"mean = {X.mean():.2f}")
print(f"var = {X.var():.2f}")
print(f"std = {X.std():.2f}")

median = 0.00
mean = 0.00
var = 1.00
std = 1.00

確率変数を引数にとる関数 $f$ の期待値 $E[f(X)]$ を計算する場合は scipy.stats.rv_continuous.expect() を使用します。

In [33]:

def f(x):
    return x ** 2 + 1


print(X.expect(f))

2.000000000000001

信頼区間

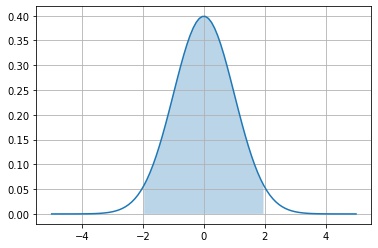
scipy.stats.rv_continuous.interval() は、 $\alpha$ が与えられたとき、 $P(median[X] – t \le X \le median[x] + t) = \alpha$ を満たす区間 $[median[X] – t, median[x] + t]$ を返します。

In [34]:

a, b = X.interval(0.95)
print(f"P[{a}, {b}]")

fig, ax = plt.subplots()

x1 = np.linspace(-5, 5, 100)
y1 = X.pdf(x1)

x2 = np.linspace(a, b, 100)
y2 = X.pdf(x2)

ax.plot(x1, y1)
ax.fill_between(x2, np.zeros_like(y2), y2, alpha=0.3)
ax.grid()

plt.show()

P[-1.959963984540054, 1.959963984540054]

台

scipy.stats.rv_continuous.support() は、確率質量関数の台 $\text{supp}(pdf) = \{x \in \R \mid f_X(x) > 0 \}$ を返します。

In [35]:

print(X.support())

(-inf, inf)

最尤推定

scipy.stats.rv_continuous.fit() でその分布の最尤推定を行います。

In [36]:

data = X.rvs(size=100)

mean, std = stats.norm.fit(data)
print(f"mean: {mean}, std: {std}")

mean: 0.18434298655426873, std: 1.038091568649953

scipy.stats.rv_continuous.fit_loc_scale() は loc, scale を推定します。

In [37]:

data = stats.uniform.rvs(loc=5, scale=1, size=1000)

loc, scale = stats.uniform.fit_loc_scale(data)
print(f"loc: {loc}, scale: {scale}")

loc: 4.986848789248153, scale: 1.0205864431590375

対数尤度関数

scipy.stats.rv_continuous.nnlf() で対数尤度関数の負をとった値を返します。 theta には、分布を表すパラメータ (loc、scale を含む) を theta = (*args, loc, scale) とタプルで渡します。

In [38]:

loc, scale = 0, 1
data = stats.norm.rvs(loc=loc, scale=scale, size=100)

nnl = stats.norm.nnlf((loc, scale), data)
print(nnl)

144.17743898141782