目次
概要
連続確率分布の1つである指数分布について解説します。
確率関数
確率変数 $X$ が次の確率密度関数をもつとき、$X$ はパラメータ $\beta$ の指数分布 (exponential distribution) に従うという。
$$ f_X(x) = \begin{cases} \beta e^{- \beta x} & x > 0 \\ 0 & その他の場合 \end{cases} $$ただし、$\Gamma(\cdot)$ はガンマ関数、$\beta > 0$ とする。
確率密度関数である
(!) 非負性
$\beta > 0$ であるから、$f_X(x) \ge 0$
(2) 規格化
$$ \begin{aligned} \int_0^\infty \beta e^{- \beta x} dx &= \beta \left[-\frac{e^{-\beta x}}{\beta}\right]_0^\infty \\ &= -\left[e^{-\beta x}\right]_0^\infty \\ &= 1 \end{aligned} $$ガンマ分布との関係
指数分布はパラメータ $\alpha = 1, \beta$ としたときのガンマ分布である。
分布関数
$x \le 0$ のとき、$f_X(x) = 0$ なので、$F_X(x) = 0$
$x > 0$ のとき、
$$ \begin{aligned} \int_0^x \beta e^{- \beta t} dt &= \beta \left[-\frac{e^{-\beta t}}{\beta}\right]_0^x \\ &= -\left[e^{-\beta t} \ \right]_0^x \\ &= 1 – e^{-\beta x} \end{aligned} $$よって、
$$ F_X(x) = \begin{cases} 1 – e^{-\beta x} & x > 0 \\ 0 & その他の場合 \end{cases} $$期待値
$$ \begin{aligned} E[X] &= \int_0^\infty x \beta e^{- \beta x} dx \\ &= \left[-x e^{-\beta x}\right]_0^\infty – \int_0^\infty -e^{-\beta x} dx \quad \because 部分積分 \\ &= \int_0^\infty e^{-\beta x} dx \\ &= \left[-\frac{1}{\beta} e^{-\beta x}\right]_0^\infty \\ &= \frac{1}{\beta} \end{aligned} $$分散
$$ \begin{aligned} E(X) &= \int_0^\infty x^2 \beta e^{- \beta x} dx \\ &= \left[-x^2 e^{-\beta x}\right]_0^\infty – 2x \int_0^\infty -e^{-\beta x} dx \quad \because 部分積分 \\ &= \int_0^\infty 2x e^{-\beta x} dx \quad \because 第1項は \lim_{x \to \infty} \ \ \frac{x^2}{e^{\beta x}} = 0 \\ &= \frac{2}{\beta} \int_0^\infty x \beta e^{-\beta x} dx \\ &= \frac{2}{\beta^2} \quad \because 第2項は E[X] \end{aligned} $$なので、
$$ \begin{aligned} Var[X] &= E[X^2] – (E[X])^2 \\ &= \frac{2}{\beta^2} – \left(\frac{1}{\beta}\right)^2 \\ &= \frac{1}{\beta^2} \end{aligned} $$標準偏差
$$ \begin{aligned} Std[X] &= \sqrt{Var[X]} \\ &= \sqrt{\frac{1}{\beta^2}} \\ &= \frac{1}{\beta} \quad \because \beta > 0 \end{aligned} $$積率母関数
$$ \begin{aligned} m_X(t) &= E[e^{tX}] \\ &= \int_0^\infty e^{tx} \beta e^{- \beta x} dx \\ &= \int_0^\infty \beta e^{- (\beta – t) x} dx \end{aligned} $$$t < \beta$ の場合、$-(\beta – t) < 0$ なので、
$$ \begin{aligned} \int_0^\infty \beta e^{- (\beta – t) x} \quad dx &= \left[-\frac{\beta}{\beta – t} e^{- (\beta – t) x} \quad \right]_0^\infty \\ &= \frac{\beta}{\beta – t} \end{aligned} $$$t = \beta$ の場合、
$$ \begin{aligned} \int_0^\infty \beta e^{- (\beta – t) x} dx &= \beta \int_0^\infty dx \\ \end{aligned} $$となり、発散する。
$t > \beta$ の場合、$-(\beta – t) > 0$ なので、
$$ \begin{aligned} \int_0^\infty \beta e^{- (\beta – t) x} \quad dx &= \left[-\frac{\beta}{\beta – t} e^{- (\beta – t) x} \quad \right]_0^\infty \end{aligned} $$は発散する。
したがって、積率母関数は $t < \beta$ のとき
$$ m_X(t) = \begin{cases} \frac{\beta}{\beta – t} & t < \beta\\ 定義されない & その他の場合 \end{cases} $$再生性
$X_1, X_2, \cdots, X_n$ が独立で同一なパラメータ $\beta$ の指数分布に従うとき、 $S = X_1 + X_2 + \cdots + X_n$ はパラメータ $n, \beta$ のアーラン分布に従う。
証明:
$X_i$ の積率母関数を $m_{X_i}(t)$ とすると、
$$ m_S(t) = \prod_{i = 1}^n m_{X_i}(t) = \left(\frac{\beta}{\beta – t}\right)^n $$これはパラメータ $n, \beta$ のアーラン分布の積率母関数と一致する。 積率母関数の一意性より、題意は示された。
scipy.stats の指数分布
scipy.stats.expon で指数分布に従う確率変数を作成できます。
In [1]:
import numpy as np
import seaborn as sns
from matplotlib import pyplot as plt
from scipy.stats import expon
sns.set(style="white")
beta = 2
X = expon(scale=1 / beta)サンプリング
In [2]:
x = X.rvs(size=5)
print(x)[0.43342208 0.57263643 0.537089 0.99356528 2.09360259]
確率質量関数
In [3]:
x = np.linspace(0, 5, 100)
y = X.pdf(x)
fig, ax = plt.subplots()
ax.plot(x, y)
ax.grid()
plt.show()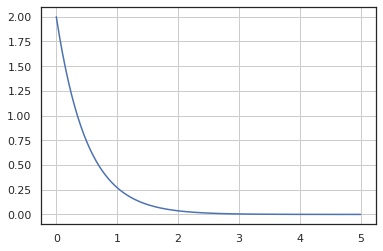
累積分布関数
In [4]:
x = np.linspace(0, 5, 100)
y = X.cdf(x)
fig, ax = plt.subplots()
ax.plot(x, y)
ax.grid()
plt.show()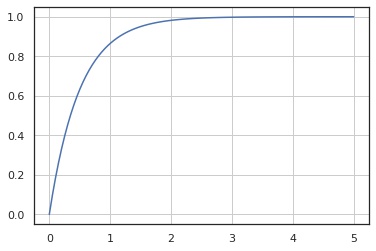
統計量
In [5]:
print("mean", X.mean())
print("var", X.var())
print("std", X.std())mean 0.5 var 0.25 std 0.5


コメント