MENU

Pytorch – 確率的勾配降下法 (SGD)、Momentum について解説

Pytorch
Pytorch ディープラーニング
  1. ホーム
  2. 機械学習
  3. Pytorch
  4. Pytorch – 確率的勾配降下法 (SGD)、Momentum について解説
目次

概要

確率的勾配降下法 (Stochastic Gradient Decent, SGD)、重み減衰 (weight decay)、Momentum、Nesterov’s Momentum について解説します。

確率的勾配降下法 (Stochastic Gradient Decent, SGD)

勾配降下法 (Gradient Decent) は、各ステップ $t$ でその時点でのパラメータ $\theta_{t – 1}$ の目標関数 (objective function) の勾配 (gradient) $\nabla_{\theta} f (\theta_{t – 1})$ を計算します。目標関数とは損失関数 (loss function) など最小化したい関数のことです。勾配は、その地点で関数の値が最も増加する方向を表しているので、勾配と反対の方向は関数の値が最も減少する方向を表しています。どのくらい動くかは学習率 (learning rate, lr) というハイパーパラメータによって決めます。

勾配降下法のアルゴリズム

$$ \begin{aligned} % 入力 &\rule{110mm}{0.4pt} \\ &\textbf{input}: \gamma \text{(lr)}, \: \theta \text{(params)}, \: f(\theta) \text{ (objective)} \: \\ % アルゴリズム &\rule{110mm}{0.4pt} \\ &\theta_0 \leftarrow \textbf{initial value} \\ &\textbf{for} \: t = 1 \: \textbf{to} \: \ldots \: \textbf{do} \\ &\hspace{5mm} g_t \leftarrow \nabla_{\theta} f_t (\theta_{t – 1}) \\ &\hspace{5mm} \theta_t \leftarrow \theta_{t – 1} – \gamma g_t \\ % 返り値 &\rule{110mm}{0.4pt} \\ &\bf{return} \: \theta_t \\ &\rule{110mm}{0.4pt} \\ \end{aligned} $$

目標関数は入力データにも依存するので、$\nabla_{\theta} f (\theta_{t – 1};x)$ と表記しますが、この $x$ に学習データのうち、どのくらいのデータを使用するかによって次の種類があります。

  • 学習データの中の1個のサンプルを使用する: 確率的勾配降下法 (Stochastic Gradient Decent, SGD)
  • 学習データの一部のサンプルを使用する: ミニバッチ勾配降下法 (Minibatch Gradient Descent)
  • 学習データのすべてのサンプルを使用する: バッチ勾配降下法 (Batch Gradient Descent)

バッチ (batch) とは学習データのすべてのサンプルのことをいうのに対し、ミニバッチ (minibatch) は一部のサンプルのことをいいます。ディープラーニングの文脈では、上記3つをあわせて確率的勾配降下法といい、使用するサンプルの数をバッチサイズ (batch size)といいます。

重み減衰 (weight decay)

目標関数を $f(\theta)$、パラメータを $\theta$ としたとき、最小化対象を $f(\theta) + \lambda \|\theta\|$ と変更することを重み減衰 (weight decay)といいます。$\lambda \|\theta\|$ は正則化項といい、$\lambda$ はどのくらい正則化を強くするかを制御するハイパーパラメータです。正則化項が加わったことにより、$\|\theta\|$ の値も小さくする制約を考慮しつつ、目標関数 $f(\theta)$ を最小化することができます。制約の追加は、ネットワークは大量のパラメータがあり自由度が高いため、過学習を防ぎ、汎化能力を高めるために行います。

通常、2ノルム $\|\cdot\|_2$ を使用する $L_2$ 正則化を使用します。2ノルムは微分した際に $\nabla_\theta \|\theta\|_2 = \frac{1}{2} \theta$ となるので、ステップ $t$ の勾配を計算する際は、実装上は目標関数の勾配に $\lambda \theta$ を加えます。

$$ g_t \leftarrow \nabla_\theta f(\theta_{t – 1}) + \lambda \theta_{t – 1} $$

Momentum

Momentum が有効の場合、今回の勾配に過去の勾配を加えます。これにより、勾配が振動して学習が不安定になる問題を防ぎます。$\mu$ の値が大きいほど過去の勾配の影響が大きくなります。

Momentum

$$ \begin{aligned} % 入力 &\rule{110mm}{0.4pt} \\ &\textbf{input}: \gamma \text{ (lr)}, \: \theta \text{ (params)}, \: f(\theta) \text{ (objective)}, \: \mu \text{ (momentum)}, \: \\ % アルゴリズム &\rule{110mm}{0.4pt} \\ &\theta_0 \leftarrow \textbf{initial value} \\ &v_0 \leftarrow 0 \\ &\textbf{for} \: t = 1 \: \textbf{to} \: \ldots \: \textbf{do} \\ &\hspace{5mm} g_t \leftarrow \nabla_{\theta} f_t (\theta_{t – 1}) \\ &\hspace{5mm} v_t \leftarrow \mu v_{t – 1} + g_t \\ &\hspace{5mm} \theta_t \leftarrow \theta_{t – 1} – \gamma v_t \\ % 出力 &\rule{110mm}{0.4pt} \\ &\bf{return} \: \theta_t \\ &\rule{110mm}{0.4pt} \\ \end{aligned} $$

$v_t$ の漸化式を展開すると、

$$ v_t = \mu^t g_1 + \mu^{t – 1} g_2 + \cdots + g_t = \sum_{i = 1}^t \mu^{t – i + 1} g_i $$

であるから、Momentum は通常の SGD の勾配をこれまでの勾配の指数移動平均に置き換えたアルゴリズムであると言えます。

※ 上記で紹介した Pytorch の実装とは異なり、元の論文 (Sutskever et. al.) では学習率を乗算する部分に Momentum の項 $\mu v_{t – 1}$ を含まないので、その点の差異があります。

$$ \begin{aligned} % 入力 &\rule{110mm}{0.4pt} \\ &\textbf{input}: \gamma \text{ (lr)}, \: \theta \text{ (params)}, \: f(\theta) \text{ (objective)}, \: \mu \text{ (momentum)}, \: \\ % アルゴリズム &\rule{110mm}{0.4pt} \\ &\theta_0 \leftarrow \textbf{initial value} \\ &v_0 \leftarrow 0 \\ &\textbf{for} \: t = 1 \: \textbf{to} \: \ldots \: \textbf{do} \\ &\hspace{5mm} g_t \leftarrow \nabla_{\theta} f_t (\theta_{t – 1}) \\ &\hspace{5mm} v_t \leftarrow \mu v_{t – 1} + g_t \\ &\hspace{5mm}\theta_t \leftarrow \theta_{t – 1} – \mu v_{t – 1} – \gamma g_t \\ % 出力 &\rule{110mm}{0.4pt} \\ &\bf{return} \: \theta_t \\ &\rule{110mm}{0.4pt} \\ \end{aligned} $$

Nesterov’s Momentum

Nesterov’s Momentum またはネステロフの加速勾配法 (Nesterov’s Accelerated Gradient method, NAG) は、Momentum のアルゴリズムにおいて、勾配を計算する位置を $\theta_{t – 1}$ から $- \gamma \mu v_{t – 1}$ だけ移動した位置 $\theta_{t – 1} – \gamma \mu v_{t – 1}$ に変更したものです。少し進んだ先で勾配の方向が変わる場合にその事を考慮に入れて、次の移動する方向を決めれるため、より効率的に移動できます。

$$ \begin{aligned} % 入力 &\rule{110mm}{0.4pt} \\ &\textbf{input}: \gamma \text{ (lr)}, \: \theta \text{ (params)}, \: f(\theta) \text{ (objective)}, \: \mu \text{ (momentum)}, \: \\ % アルゴリズム &\rule{110mm}{0.4pt} \\ &\theta_0 \leftarrow \textbf{initial value} \\ &v_0 \leftarrow 0 \\ &\textbf{for} \: t = 1 \: \textbf{to} \: \ldots \: \textbf{do} \\ &\hspace{5mm} g_t \leftarrow \nabla_\theta f_t(\theta_{t – 1} – \gamma \mu v_{t – 1}) \\ &\hspace{5mm} v_t \leftarrow \mu v_{t – 1} + g_t \\ &\hspace{5mm} \theta_t \leftarrow \theta_{t – 1} – \gamma v_t \\ % 出力 &\rule{110mm}{0.4pt} \\ &\bf{return} \: \theta_t \\ &\rule{110mm}{0.4pt} \\ \end{aligned} $$

Nesterov’s Momentum

以下の式変形を行うと、Pytorch の SGD に記載されているアルゴリズムと一致します。

$\theta’_t = \theta_t – \gamma \mu v_t$ とおくと、

$$ \begin{aligned} \theta’_t &= \theta_t – \gamma \mu v_t \\ &= \theta_{t – 1} – \gamma v_t – \gamma \mu v_t \\ &= \theta’_{t – 1} + \gamma \mu v_{t – 1} – \gamma v_t – \gamma \mu v_t \quad \because \theta’_{t – 1} = \theta_{t – 1} – \gamma \mu v_{t – 1} \\ &= \theta’_{t – 1} – \gamma (v_t – \mu v_{t – 1} + \mu v_t) \\ &= \theta’_{t – 1} – \gamma (\nabla_{\theta’} f(\theta’_{t – 1}) + \mu v_t) \quad \because v_t – \mu v_{t – 1} = \nabla_{\theta’} f(\theta’_{t – 1}) \\ \end{aligned} $$

よって

$$ \begin{aligned} v_t &= \mu v_{t – 1} + \nabla_{\theta’} f(\theta’_{t – 1}) \\ \theta’_t &= \theta’_{t – 1} – \gamma (\nabla_{\theta’} f(\theta’_{t – 1}) + \mu v_t) \\ \end{aligned} $$

Nesterov’s Momentum のアルゴリズム (Pytorch 版)

$$ \begin{aligned} % 入力 &\rule{110mm}{0.4pt} \\ &\textbf{input}: \gamma \text{ (lr)}, \: \theta \text{ (params)}, \: f(\theta) \text{ (objective)}, \: \mu \text{ (momentum)}, \: &\hspace{13mm} \\ % アルゴリズム &\rule{110mm}{0.4pt} \\ &\theta_0 \leftarrow \textbf{initial value} \\ &v_0 \leftarrow 0 \\ &\textbf{for} \: t = 1 \: \textbf{to} \: \ldots \: \textbf{do} \\ &\hspace{5mm} g_t \leftarrow \nabla_{\theta} f (\theta_{t – 1}) \\ &\hspace{5mm} v_t \leftarrow \mu v_{t – 1} + g_t \\ &\hspace{5mm} \theta_t \leftarrow \theta_{t – 1} – \gamma (g_t + \mu v_t) \\ % 出力 &\rule{110mm}{0.4pt} \\ &\bf{return} \: \theta_t \\ &\rule{110mm}{0.4pt} \\ \end{aligned} $$

※ 公式ドキュメントの記載において、$g_t \leftarrow g_{t – 1} + \mu b_t$ と記載されていますが、ソースコードを見ると、$g_t \leftarrow g_t + \mu b_t$ が正しいと思われます。

Pytorch で SGD を使用する

確率的勾配降下法は、SGD で実装されています。

torch.optim.SGD(params, lr, momentum=0, dampening=0, weight_decay=0, nesterov=False)
パラメータ 意味 初期値 範囲
lr 学習率 0 0より大きい小数
momentum momentum の係数 0 0以上の小数
dampening momentum の係数 0 小数
weight_decay weight decay の係数 0 0以上の小数
nesterov Nesterov’s Momentum を有効にするかどうか FALSE bool

dampening は Momentum の値を更新する部分で $v_t \leftarrow \mu v_{t – 1} + (1 – \text{dampening}) g_t$ として、加算される現在の勾配の値の影響を小さくするパラメータです。dampening=0 で前の項で紹介したアルゴリズムと同じになります。

SGD を使用して関数の最小値を探す

$f(x, y) = x^2 + y^2 + xy$ という関数の最小値を SGD を使用して探索してみます。

この関数は次のような形状をしています。

In [1]: 
import torch


def f1(x):
    return x[0] ** 2 + x[1] ** 2 + x[0] * x[1]


def sgd_optimize(f, init, lr, max_iter=100, **params):
    x = torch.tensor(init, dtype=torch.float32, requires_grad=True)
    optimizer = torch.optim.SGD([x], lr, **params)

    xs = [x.clone()]
    x_old = x.clone()
    for i in range(max_iter):
        # 関数値を計算する。
        y = f(x)
        # 勾配を計算する。
        optimizer.zero_grad()
        y.backward()
        # 更新する。
        optimizer.step()

        if (x - x_old).norm() < 0.01:
            break  # 収束した場合は途中で抜ける
        x_old = x.clone()

        xs.append(x.clone())

    xs = torch.stack(xs).detach().numpy()

    return xs

xs = sgd_optimize(f1, init=[3, 7], lr=0.1)
  1. torch.tensor(init, dtype=torch.float32, requires_grad=True) で変数を定義します。requires_grad=True とした場合、勾配の計算を行えるテンソルになります。
  2. optimizer = torch.optim.SGD([x], lr) で SGD の Optimizer を定義します。第1引数には最適化を行う変数をリストで渡します。
  3. y = f(x) で x に対する関数値を計算します。
  4. y.backward() で x に対する f(x) の勾配を計算します。計算前に optimizer.zero_grad() を呼び出し、前回のステップの勾配情報をクリアする必要があります。勾配をクリアしない場合、前回の勾配に今回の勾配が加算される形になります。
  5. optimizer.step() で計算された勾配を元に、SGD で変数 x を更新します。
  6. 変数 $x$ の移動量 $\|x_{old} – x\|$ を計算し、この値が十分小さい場合は収束したと判断して、最大のステップ数に達していない場合でも途中で抜けます。
  7. 上記のステップを指定回数繰り返します。

変数 x の推移を等高線及びグラフに描画し、確認します。

In [2]: 
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.lines import Line2D
from mpl_toolkits.mplot3d import Axes3D


def draw_history(f, xs, elev=70, azim=-70):
    fig = plt.figure(figsize=(14, 6))

    X1, X2 = np.mgrid[-10:11, -10:11]
    Y = f((X1, X2))  # 各点での関数 f の値を計算する。

    ys = [f(x) for x in xs]

    # 勾配のベクトル図を作成する。
    ax1 = fig.add_subplot(121)
    ax1.set_title("Contour")
    ax1.set_xticks(np.arange(-10, 11, 2))
    ax1.set_yticks(np.arange(-10, 11, 2))
    ax1.set_xlabel("$x$", fontsize=15)
    ax1.set_ylabel("$y$", fontsize=15)
    ax1.grid()
    ax1.plot(xs[:, 0], xs[:, 1], "ro-", mec="b", mfc="b", ms=4)
    contours = ax1.contour(X1, X2, Y, levels=15)
    ax1.clabel(contours, inline=1, fontsize=10, fmt="%.2f")

    # グラフを作成する。
    ax2 = fig.add_subplot(122, projection="3d")
    ax2.set_title("Surface")
    ax2.set_xlabel("$x$", fontsize=15)
    ax2.set_ylabel("$y$", fontsize=15)
    ax2.set_zlabel("$z$", fontsize=15)
    ax2.plot(xs[:, 0], xs[:, 1], ys, "ro-", mec="b", mfc="b", ms=4)
    ax2.plot_surface(X1, X2, Y, alpha=0.3, edgecolor="black")
    ax2.view_init(elev=elev, azim=azim)

    plt.show()


draw_history(f1, xs)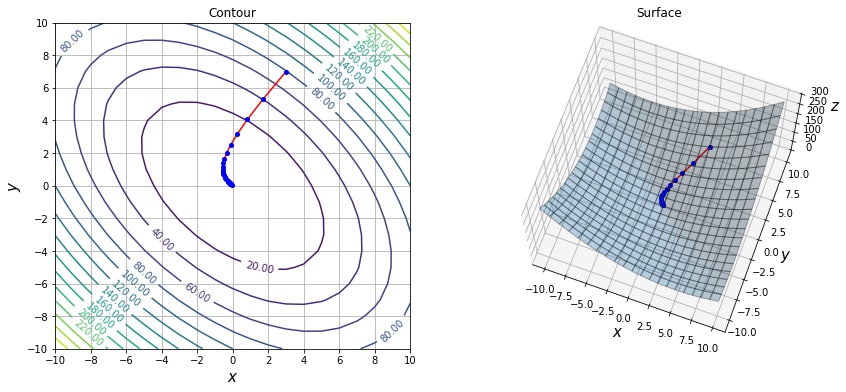

学習率の影響

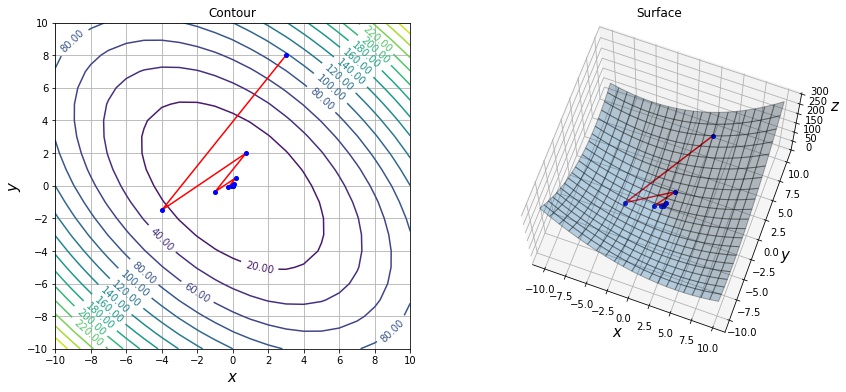
学習率がパラメータの更新にどう影響するかを可視化して考察します。 学習率が大きい場合は、移動方向で最も関数が最小となる点を通り過ぎてしまうため、下記のように振動しながら収束します。

In [3]: 
xs = sgd_optimize(f1, init=[3, 8], max_iter=1000, lr=0.5)
print(len(xs))
draw_history(f1, xs)
12

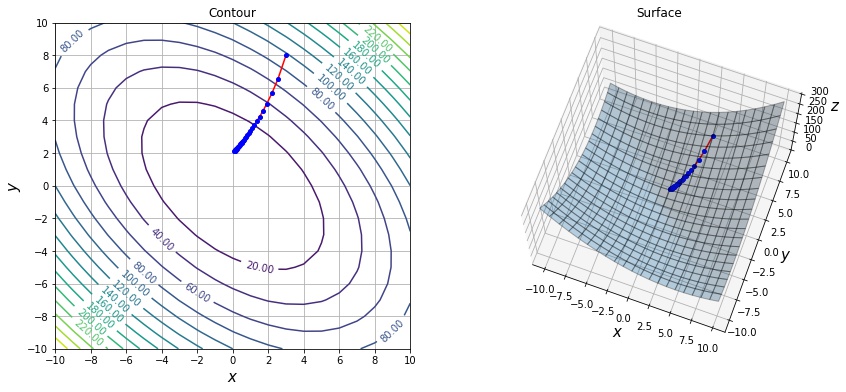
逆に学習率が小さい場合は、一回に移動する量が少ないため、収束までに多くのステップ数が必要です。

In [4]: 
xs = sgd_optimize(f, init=[3, 8], max_iter=1000, lr=0.01)
print(len(xs))
draw_history(f1, xs)
42

局所解、鞍点

凸関数でない場合、極小点が大域解であることが保証されませんが、ニューラルネットワークの損失関数は通常、凸関数でありません。勾配降下法は局所的に関数の値を小さくする方向に逐次移動するアルゴリズムであるため、学習率によっては局所解や鞍点に嵌ると抜け出せなくなります。

下記の例は $f(x, y) = x^3 + y-3 + 3 x^2 – 3 y^2 – 8$ という関数の例です。この関数は $(0, 0), (0, 2), (-2, 0), (-2, 2)$ という4点で勾配が $\nabla_x f(x) = \mathbf{0}$ になります。SGD を実行すると、$(0, 2)$ の局所解に嵌ってしまい更新が停止します。

In [5]: 
def f2(x):
    return x[0] ** 3 + x[1] ** 3 + 3 * x[0] ** 2 - 3 * x[1] ** 2 - 8


xs = sgd_optimize(f, init=[6, 4], max_iter=100, lr=0.01)
draw_history(f2, xs, elev=20, azim=-50)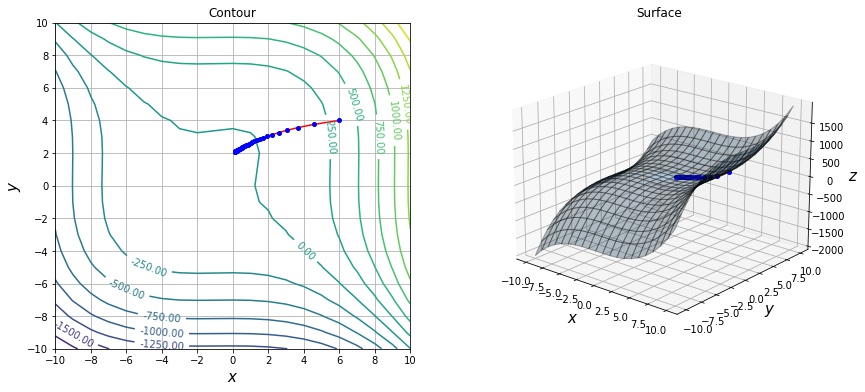

Momentum の影響

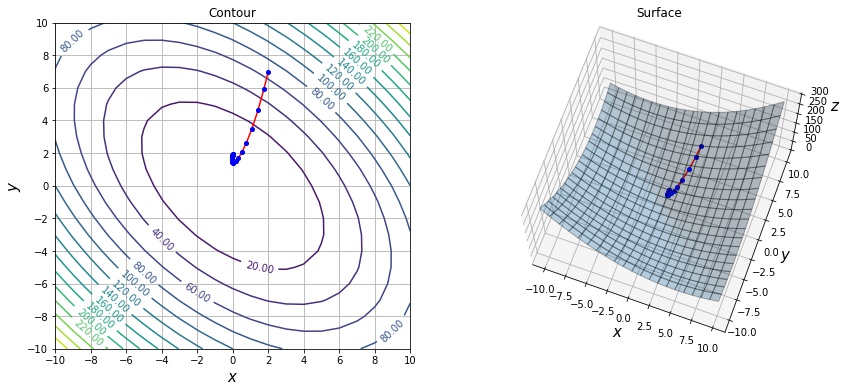
勾配が急なところでは、Momentum により1回の移動量が多くなるため、解に早くたどり着けます。

In [6]: 
def f3(x):
    return 0.05 * x[0] ** 2 + x[1] ** 2


xs = sgd_optimize(f, init=[2, 7], lr=0.01, momentum=0.6)
print(len(xs))
draw_history(f1, xs)
28

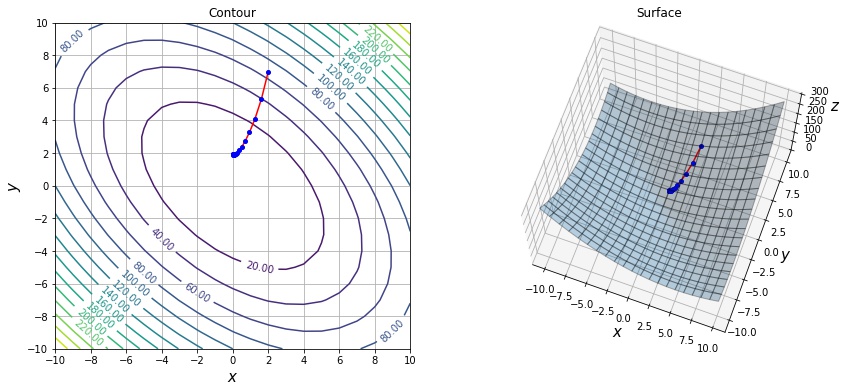
Nesterov’s Momentum の場合、少し進んだ先での勾配の方向を考慮に入れて移動できるため、Momentum にあった行き過ぎて折り返すということがなくなるため、より少ないステップで収束しています。

In [7]: 
xs = sgd_optimize(f, init=[2, 7], lr=0.01, momentum=0.6, nesterov=True)
print(len(xs))
draw_history(f1, xs)
17

パラメータごとに各種係数を変更したい場合

torch.optim.SGD() の第1引数に dict の list を指定する方式で、パラメータごとに学習率などの係数を指定できます。

params = [
    {"params": パラメータA, "lr": 0.001},
    {"params": パラメータB},
    {"params": パラメータC},
]

optimizer = torch.optim.SGD(params, lr=0.01)

このようにした場合、パラメータAだけ学習率は 0.001 になり、個別に指定していないパラメータB、パラメータCの学習率は0.01になります。

参考

Pytorch
Pytorch ディープラーニング

関連記事

コメント

コメントする

目次