概要
機械学習の勾配効果法について解説し、実装例を紹介します。
勾配法
最適化
与えられた制約条件のもとで関数の値を最大化または最小化する変数の値を求めることを最適化といいます。
勾配法の仕組み
$\mathbb{R}^n$ の開集合 $\Omega$ 上で $n$ 次元関数 $f: \Omega \to \mathbb{R}$ が定義されているとし、この関数の極小値を求めることを考えます。
今、ある点 $\boldsymbol{x}_k$ にいる場合、その点の勾配 $\nabla f (\boldsymbol{x}_k)$ は点 $\boldsymbol{x}_k$ の近傍で関数の値を最も増加させる「最急上昇方向 (steepest ascent)」であるから、その反対方向 $-\nabla f (\boldsymbol{x}_k)$ は関数の値を最も減少させる「最急降下方向 (steepest descent)」です。
よって、点 $\boldsymbol{x}_k$ から勾配と逆方向に進んで、新しい点 $\boldsymbol{x}_{k + 1}$ に移動することで関数の値を減少させることができます。
$$ \boldsymbol{x}_{k + 1} = \boldsymbol{x}_k -\alpha \nabla f (\boldsymbol{x}_k) $$上記の更新を1回行うことを1反復 (iteration)といます。
$\alpha \in \mathbb{R}^+$ は勾配方向にどのくらい進むかを表すスカラーであり、ステップ幅といいます。各反復で関数値が減少するよう移動したいので、$f(\boldsymbol{x}_k) \ge f(\boldsymbol{x}_{k + 1})$ を満たす $\alpha$ を選択します。ステップ幅は反復ごとに変更してもよいです。反復は点が極小点に到達するまで繰り返します。
極小点に到達したかどうかは、極値点では勾配が $\nabla f (\boldsymbol{x}_k) = \boldsymbol{0}$ となることを利用して判定を行います。 数値計算においては、厳密に $\boldsymbol{0}$ になることはないので、十分 $\boldsymbol{0}$ に近ければ収束したと判定し、反復を終了します。
これまでの一連の流れを整理すると、以下のようになる。
アルゴリズム 最急降下法
- 初期点 $\boldsymbol{x}_0$ を決める。
- 勾配 $\nabla f (\boldsymbol{x}_k)$ を計算し、$\nabla f (\boldsymbol{x}_k) = \boldsymbol{0}$ の場合、終了する。
点を次のように更新する。
$$ \boldsymbol{x}_{k + 1} = \boldsymbol{x}_k -\alpha \nabla f (\boldsymbol{x}_k) $$
2 に戻る。
また、$n$ 次元関数 $f: \Omega \to \mathbb{R}$ の極大点を求める勾配法は「最急上昇法」といいます。
アルゴリズム 最急上昇法
- 初期点 $\boldsymbol{x}_0$ を決める。
- 勾配 $\nabla f (\boldsymbol{x}_k)$ を計算し、$\nabla f (\boldsymbol{x}_k) = \boldsymbol{0}$ の場合、終了する。
点を次のように更新する。
$$ \boldsymbol{x}_{k + 1} = \boldsymbol{x}_k + \alpha \nabla f (\boldsymbol{x}_k) $$
2 に戻る。
ステップ幅の決め方
勾配法ではステップ幅 $\alpha$ をどのように決めるかが問題になります。 値が小さすぎると収束までに時間がかかってしまい、逆に大きすぎるといつまでの収束しないか発散してしまいます。
ステップ幅を直線探索で決める
1つの方法として、探索方向で関数値が最小となるようにステップ幅を選ぶ方法が考えられます。これを直線探索 (line search)といいます。 今、点 $\boldsymbol{x}$ にいる場合、探索方向の直線上の点は $\boldsymbol{x}'(\alpha) = \boldsymbol{x} -\alpha \nabla f (\boldsymbol{x}), \ \alpha \in \mathbb{R}^+$ と表せます。これを探索直線 (search line)といいます。この探索直線上で関数値が最小となる
$$ \argmin_{\alpha} f(\boldsymbol{x}'(\alpha)) $$を求めます。これを満たす点は極小点なので、$F(\alpha) = f(\boldsymbol{x}'(\alpha))$ とおくと、$\frac{dF(\alpha)}{d\alpha} = 0$ を満たします。
定理 直線探索でステップ幅を決めた場合、勾配は1つ前の勾配と直交する。
$\boldsymbol{x} = (x_1, x_2, \cdots, x_n)^T$ とすると、関数 $F$ は $x_1, x_2, \cdots, x_n$ によって決まり、$x_1, x_2, \cdots, x_n$ は $\alpha$ によって決まるので連鎖律が適用でき、
$$ \frac{dF(\alpha)}{d\alpha} = \sum_{i=1}^{n} \frac{\partial f}{\partial x’_i} \frac{\partial x’_i}{\partial \alpha} $$$x’_i(t) = x_i + \alpha \frac{\partial f}{\partial x}$ であるから、$\frac{\partial x’_i}{\partial \alpha} = \frac{\partial f}{\partial x}$ となる。 よって、先程の式に代入すると、
$$ \frac{dF(t)}{dt} = \sum_{i=1}^{n} \frac{\partial f}{\partial x’} \frac{\partial f}{\partial x_i} = (\nabla f(\boldsymbol{x}’), \nabla f(\boldsymbol{x})) $$よって、探索直線上で極小値をとる点では、$(\nabla f(\boldsymbol{x}), \nabla f(\boldsymbol{x}’)) = 0$ を満たします。 つまり、探索方向 $\nabla f(\boldsymbol{x})$ と探索直線の極小値をとる点での勾配 $\nabla f(\boldsymbol{x}’)$ が直交することを意味しています。
直線探索を可視化して理解する
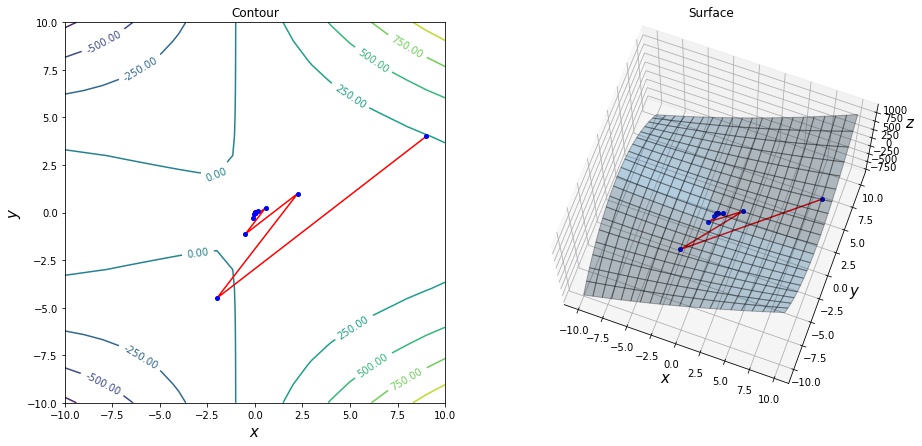
2変数関数 $f(x_1, x_2) = x_1^2 + x_2^2 + x_1 x_2$ を定義します。 この勾配は $\nabla f(x_1, x_2) = \left(2 x_1 + x_2, 2 x_2 + x_1\right)^T$ です。
関数 $f$ を描画します。
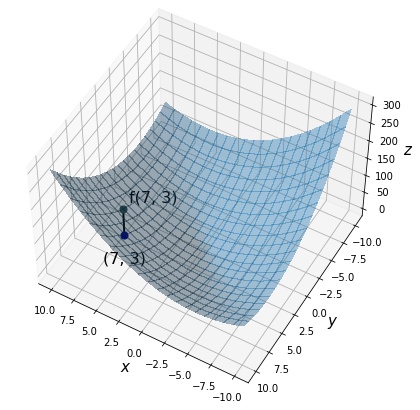
今、点 $(7,3)$ にいるとしたとき、対応する関数値 $f(7,3)$ を描画します。
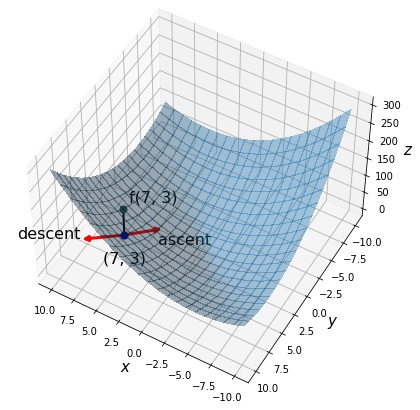
点 $(7, 3)$ における勾配は $\nabla f(7, 3) = (17, 13)^T$ です。 最急上昇方向 $\nabla f(7, 3) = (17, 13)^T$、最急降下方向 $-\nabla f(7, 3) = (17, 13)^T$ を描画します。
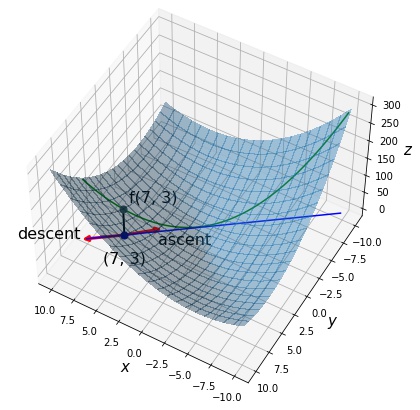
探索直線上の点は $\nabla (3, 7) – \alpha (17, 13)^T$ と表せます。 青の直線が探索直線、緑の線が探索直線上の各点に対応する関数値を表しています。
直線探索による勾配法を実装する
数値計算は丸め誤差があるため、勾配の値が厳密に $\boldsymbol{0}$ になりません。そのため、勾配の各要素と $\boldsymbol{0}$ の差が 0.001 未満であれば、収束したと判断しています。直線探索を行い、ステップ幅を決めるには scipy.optimize.line_search() を使用します。
import numpy as np
from scipy.optimize import line_search
def gradient_decent(f, f_prime, init_x, max_iters=100):
x = np.array(init_x, dtype=float) # 初期点
xs, ys = [], [] # x, f(x) の履歴
for itr in range(1, max_iters + 1):
xs.append(x), ys.append(f(x))
delta = f_prime(x) # 勾配を計算する。
if np.all(np.abs(delta) < 0.001):
break # 極値に到達
# 直線探索でステップ幅を決定する。
step = line_search(f, f_prime, xk=x, pk=-delta)[0]
x = x - step * delta # 更新する。
return itr, np.array(xs), np.array(ys)
# 関数及び勾配を定義する。
def f(x):
x1, x2 = x
return x1 ** 2 + x2 ** 2 + x1 * x2
def f_prime(x):
x1, x2 = x
return np.array([2 * x1 + x2, 2 * x2 + x1])
# 勾配法を実行する。
num_itrs, xs, ys = gradient_decent(f, f_prime, init_x=np.array([7.0, 3.0]))
print("iterations", num_itrs)iterations 4
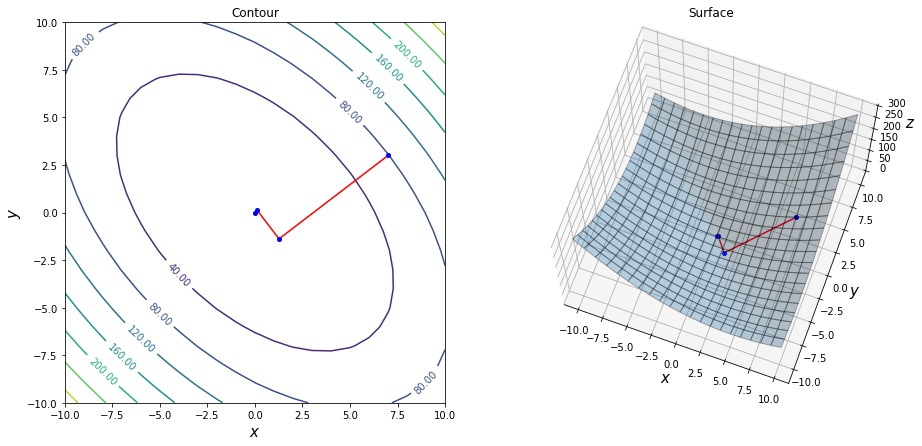
結果を見ると、先程の定理の通り、ある反復の勾配とその前後の反復の勾配が直交していることが確認できます。
ステップ幅を定数で決める
反復ごとに直線探索を行うのは、計算量が多くなってしまいます。その代わりにステップ幅を適当な小さい値に設定する方法が一般的に用いられています。この定数の適切な値は関数の性質によって変わってきます。以下、ステップ幅を定数 0.1 とした場合の勾配法を実装します。
import numpy as np
def gradient_decent(f, f_prime, init_x, step=0.1, max_iters=100):
x = np.array(init_x, dtype=float) # 初期点
xs, ys = [], [] # x, f(x) の履歴
for itr in range(1, max_iters + 1):
xs.append(x), ys.append(f(x))
delta = f_prime(x) # 勾配を計算する。
if np.all(np.abs(delta) < 0.001):
break # 極値に到達
x = x - step * delta # 更新する。
return itr, np.array(xs), np.array(ys)
# 関数及び勾配を定義する。
def f(x):
x1, x2 = x
return x1 ** 2 + x2 ** 2 + x1 * x2
def f_prime(x):
x1, x2 = x
return np.array([2 * x1 + x2, 2 * x2 + x1])
# 勾配法を実行する。
num_itrs, xs, ys = gradient_decent(f, f_prime, init_x=np.array([7.0, 3.0]))
print("iterations", num_itrs)iterations 74
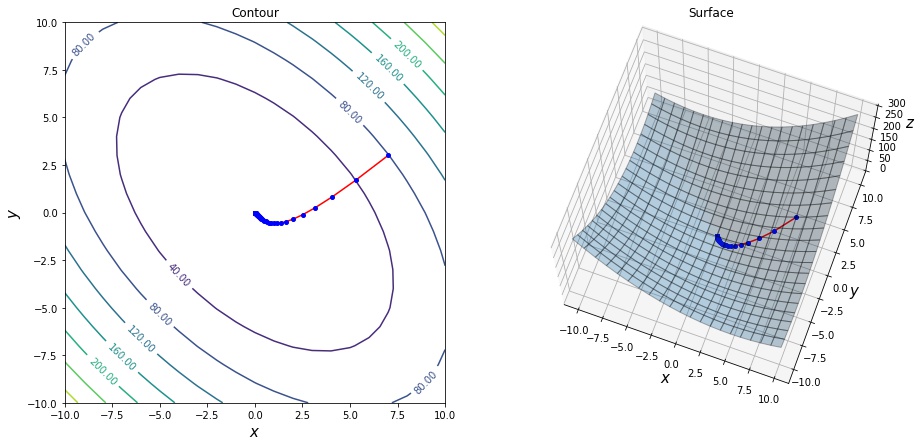
勾配法の欠点について
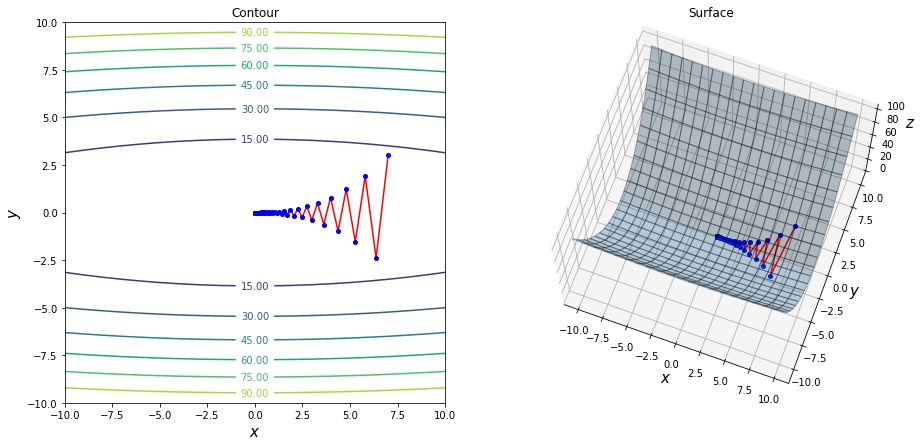
関数の形状によっては収束に必要な反復回数が増えてしまう
例えば、2変数関数 $f(x_1, x_2) = 0.05 x_1^2 + x_2^2$ は以下の画像のような谷の形をしています。このような関数に対して、勾配法を実行すると、谷と垂直の方向の勾配はなだらかのため、極値点に到達するまでに多くの反復回数が必要となります。
iterations 71
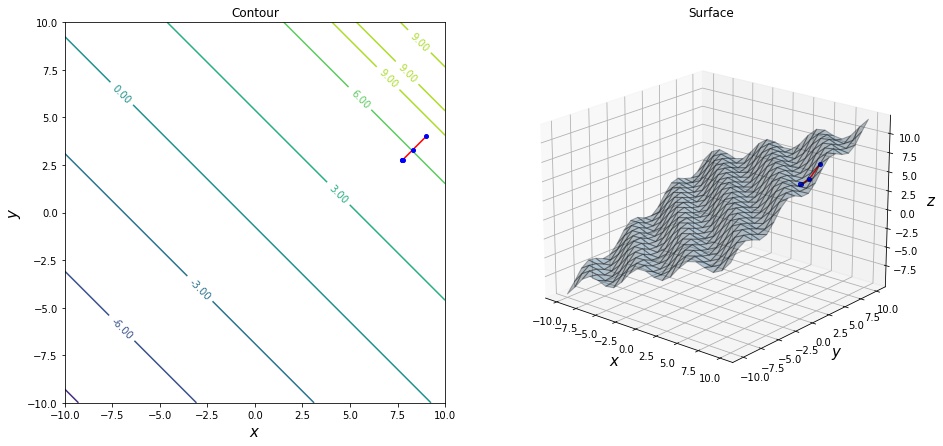
局所解に収束してしまう
収束判定条件が勾配が $\boldsymbol{0}$ の場合であるため、極値が複数存在する場合、最小値でない極小値に収束しまう場合があります。 例えば、2変数関数 $f(x_1, x_2) = \sin(x_1 + x_2) + 0.5 (x_1 + x_2)$ は以下の波状の関数ですが、極小値が複数存在するため、勾配法を実行した際にそこでアルゴリズムが終了してしまいます。
iterations 5
鞍点に収束してしまう
収束判定条件が勾配が $\boldsymbol{0}$ の場合であるため、鞍点または停留点に収束してしまう場合があります。 例えば、2変数関数 $f(x_1, x_2) = x_1^2 + x_2^2 + x_1 x_2^2$ は $(0, 0)^T$ の鞍点を持つ関数ですが、鞍点で勾配の値が $\boldsymbol{0}$ となるため、勾配法を実行した際にそこでアルゴリズムが終了してしまいます。
iterations 16


コメント