麻雀 – 何切る問題の期待値の計算方法について

概要

麻雀における手牌の期待値の計算方法について考察します。

何切る問題

何切る問題とは、麻雀で手牌が14枚の場合にどの牌を切るべきかを問う問題です。以下では、問題を簡単にするために、他プレイヤーは考慮せず、終局または和了まで打牌と自摸を繰り返す「一人麻雀」を対象とします。この場合、点数を重視したい場合は和了時の点数期待値が最大化する打牌を、トップでオーラスの場合は和了確率を最大化する打牌を選択するのがよいでしょう。実戦では、点棒、牌の危険度、場に出てる牌の枚数など多くの情報を元に総合的に判断する必要がありため、一人麻雀における最善手が必ずしも実戦での最善手とはなりません。ですが、「一人麻雀」において牌効率を高くする打ち筋を身につけることは、点数を得られる機会を増やすことに繋がるため、麻雀を上達する上で重要な技術要素の1つであると考えられます。

受入枚数と期待値

何切る問題を考える際は受入枚数を考える場合が多いと思いますが、受入枚数が最大の打牌を選択することは1向聴下げる確率を最大化することであり、点数を得るという最終的な目的を考えた場合に、必ずしも最善手とは限りません。一気通貫や全帯幺などの役を狙い、点数を得るためには受入枚数が少ない打牌を選択したほうがよいこともあります。そこで、期待値や和了確率という考え方を取り入れることにより、何切る問題に対してより幅広い視点で考察することができるようになります。

麻雀何切るシミュレーター

以下で麻雀における期待値の計算方法について解説しますが、1向聴以上では膨大なパターンを考える必要が出てくるため、手計算で求めるのは現実的ではありません。そのため、期待値などを自動で計算するアプリ「麻雀何切るシミュレーター」を用意しました。

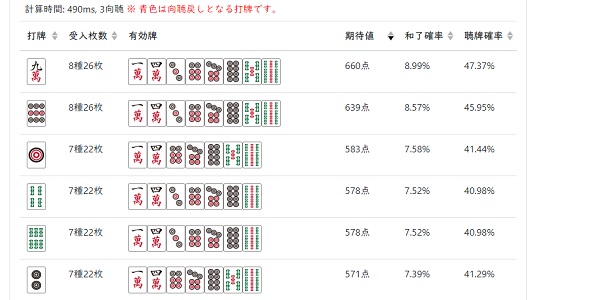
麻雀何切るシミュレーター は、各打牌の受入枚数、点数期待値、和了確率、聴牌確率を計算します。何切る問題を検討する際にもしよかったらご利用ください。

一人麻雀

一人麻雀の定義は、あらさんが公開されている牌効率練習ソフト 一人麻雀練習機 から引用させていただいています。以下に詳細を記載しますが、簡単に言うと、終局または和了まで自摸と打牌を繰り返す麻雀のことです。これから考える期待値については、この一人麻雀の設定を元に計算します。

• 他家は考慮しません。
• 自摸数は最大17回です。 4人麻雀の場合、東家、南家は18回、西家と北家は17回自摸れるので、最初13枚の手牌から18回自摸れるものとします。 何切る問題を考える際は手牌が14枚になっているので、1巡目の場合はすでに1回自摸を行っているため、最大であと17回自摸が行えます。
• 副露 (ポン、チー、暗槓、明槓、加槓) は考慮しません。ただし、何切るを考える時点で、副露している手牌は設定可能です。
• 積み棒、不聴罰符、立直棒は考慮しません。
• 東家の場合は親、それ以外の場合は子として点数計算します。
• 赤牌の自摸は考慮します。
• ドラ、槓ドラは考慮します。
• ダブル立直、一発、海底撈月は考慮します。
• 裏ドラは考慮します。※1
• 向聴戻し、手変わりは考慮します。※2
• 立直は必ずします。つまり、和了役として立直、門前清自摸和が必ずつきます。

---

• ※1: 槓ドラがある場合、裏ドラが乗る期待値を厳密に計算することは計算量が多くなってしまうため、平和系での裏ドラが乗る枚数に関する統計データを元に計算します。
• ※2: 計算量の観点で、現在の向聴数 + 2枚までの牌交換という条件で探索します。例えば、今2向聴数の場合、最短で3枚交換すると和了れます。そのため、+1 枚余分に交換できるものとして、向聴戻しや手変わりは和了までのいずれかのタイミングで1回のみ考慮することになります。また、和了を逃して向聴戻しすることは考慮しません。(安目を引いてしまった場合に和了逃しするなど)

点数期待値

何切る問題の点数期待値の計算方法について解説します。

聴牌している手牌 (13枚) の期待値

聴牌している13枚の手牌「222567m345p3367s」について考えます。向聴戻しや手変わりを考えない場合、ここから手牌が遷移できるパターンとして以下が考えられます。

受入枚数は 5s が4枚、8s が4枚の合計8枚です。まず、5s 自摸の期待値を計算するために、2巡目 ～ 18巡目に 5s を自摸る確率をそれぞれ計算します。

• 2巡目に 5s を引く確率は、場にまだ見えていない牌は手牌の14枚とドラ表示牌1枚を除いた $136 – 14 – 1 = 121$ 枚で、5s は4枚残っているので、$\frac{4}{121}$ です。
• 3巡目に 5s を引く確率は、「2巡目までに有効牌 5s または 8s 以外の牌を引いた確率 $\frac{121 – 8}{121}$」と「3巡目に 5s を引く確率 $\frac{4}{120}$」を乗算して計算します。1巡ごとに場に見えてる牌が1枚減っていくことに注意してください。
• 4巡目に 5s を引く確率は、同様に「3巡目までに有効牌 5s または 8s 以外の牌を引いた確率 $\frac{121 – 8}{121} \times \frac{120 – 8}{120}$」と「4巡目に 5s を引く確率 $\frac{4}{119}$」を乗算して計算します。
• 5巡目以降も同様に計算します。

5s、8s 自摸のどちらの場合も点数は立直、門前清自摸和、断么九で親の30符3翻で $6000$ 点です。 5s 自摸の期待値は各巡目に 5s を引く確率に和了点 $6000$ 点を乗算して、総和をとります。

2巡目に 5s を引く確率 * 6000
+ 3巡目に 5s を引く確率 * 6000
...
+ 18巡目に 5s を引く確率 * 6000
= 2141.18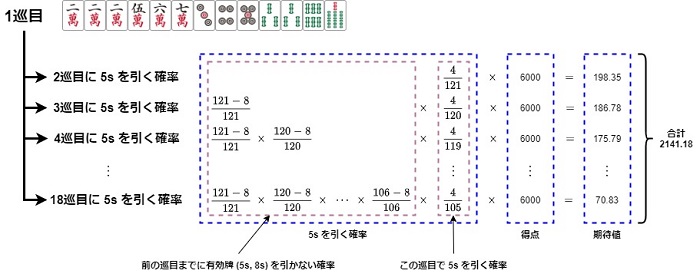

同様に 8s 自摸の場合も、8s は4枚残っており、点数も $6000$ 点で変わらないので、$2141.18$ 点になります。 したがって、1巡目に「222567m345p3367s」である期待値は $2141.18 + 2141.18 = 4282.36$ 点です。

手牌 (14枚) の期待値

「222567m345p33667s」の期待値について考えます。 向聴数が変わらない打牌は 6s, 7s です。先程、7s 打牌後の「222567m345p3367s」の期待値を計算したので、同様に 6s 打牌後の13枚の手牌「222567m345p3366s」の期待値も計算します。

受入枚数は 3s が2枚、6s が2枚の合計4枚です。3s、6s 自摸のどちらの場合も点数は立直、門前清自摸和、断么九で親の30符3翻で $6000$ 点です。期待値は $1376.26 + 1376.26 = 2752.52$ 点です。

打牌後の手牌の期待値は以下のようになりました。

• 打 6s: $4282.36$ 点 受入枚数8枚
• 打 7s: $2752.52$ 点 受入枚数4枚

「222567m345p33667s」の期待値は、打牌後の13枚の期待値が最大となる打牌の期待値 (今回の場合、打 6s の $4282.36$) を採用します。

1向聴以上手牌 (13枚) の期待値

例として、1向聴の13枚の手牌「手牌: 222567m34p3366s北 場風牌: 東, 自風牌: 東, 1巡目, ドラ: 南」について考えます。向聴戻しや手変わりを考えない場合、ここから手牌が遷移できるパターンとして以下が考えられます。

受入枚数は 2p, 5p が各4枚、3s, 6s が各2枚の合計12枚です。まず、2p 自摸の期待値を計算するために、2巡目 ～ 18巡目に 2p を自摸る確率をそれぞれ計算します。

• 2巡目に 2p を引く確率は、場にまだ見えていない牌は手牌の14枚とドラ表示牌1枚を除いた $136 – 14 – 1 = 121$ 枚で、2p は4枚残っているので、$\frac{4}{121}$ です。
• 3巡目に 2p を引く確率は、「2巡目までに有効牌 2p, 5p, 3s, 6s 以外の牌を引いた確率 $\frac{121 – 20}{121}$」と「3巡目に 2p を引く確率 $\frac{4}{120}$」を乗算して計算します。
• 4巡目に 2p を引く確率は、同様に「3巡目までに有効牌 2p, 5p, 3s, 6s 以外の牌を引いた確率 $\frac{121 – 20}{121} \times \frac{120 – 20}{120}$」と「4巡目に 2p を引く確率 $\frac{4}{119}$」を乗算して計算します。
• 5巡目以降も同様に計算します。

先程と異なるのは、得点の部分が遷移後の手牌の期待値に置き換わる点です。 5s 自摸の期待値は各巡目に 5s を引く確率にその巡目で手牌が 222567m234p3366s北 である期待値を乗算して、総和をとります。

2巡目に 5s を引く確率 * 2巡目に 222567m234p3366s北 である期待値
+ 3巡目に 5s を引く確率 * 3巡目に 222567m234p3366s北 である期待値
...
+ 18巡目に 5s を引く確率 * 18巡目に 222567m234p3366s北 である期待値
= 523.95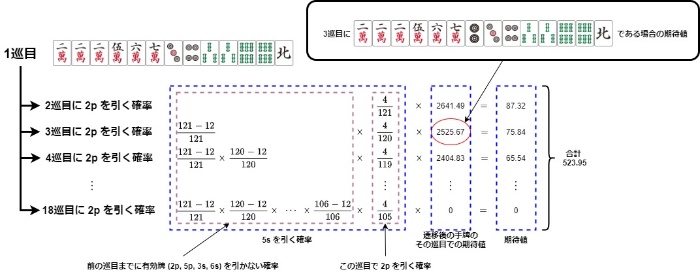

同様に 5p、3s、6s についても計算すると、

• 2p 自摸: $523.95$ 点
• 5p 自摸: $523.95$ 点
• 3s 自摸: $436.57$ 点
• 6s 自摸: $436.57$ 点

となり、これの和をとった $1921.04$ 点が期待値ということになります。

実装について

何切るシミュレーターで使用している C++ の実装例は nekobean/mahjong-cpp の mahjong-cpp/expectedvaluecalculator.cpp にあります。

• 期待値を計算するためには現在の手牌から和了までのすべての遷移パターンを探索する必要があります。自摸を行う draw() 関数及び打牌を行う discard() 関数を定義し、和了まで交互に再帰的に呼び出します。
• 手牌で現在の巡目が 1 ~ 17 巡目である期待値は一度に計算可能です。現在の巡目が18巡目で和了形でない場合は期待値0なので計算する必要があります。

手牌が14枚の期待値計算

手牌の打牌候補のうち、最も期待値が高い打牌をその手牌の期待値とします。以下が擬似コードです。 ※ 擬似コードの配列の添字は1始まりとします。

def discard(hand):
    # 手牌 hand で現在の巡目が 1 ~ 17 巡目のときの期待値
    exp_values = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

    # 手牌 hand の打牌一覧を取得する。
    discard_tiles = get_discard_tiles(hand)

    for tile in discard_tiles:
        # 手牌から tile を除く。
        remove_tile(hand, tile)
        # 打牌して13枚になった手牌の期待値を計算する。
        next_exp_values = draw(hand)

        for i = 1 to 17:
            # 手牌 hand の i 巡目の期待値
            exp_values[i] = max(exp_values[i], next_exp_values[i])

        # 手牌から除いた tile を戻す。
        add_tile(hand, tile)

    return exp_values

手牌が13枚の期待値計算

手牌の打牌候補のうち、最も期待値が高い打牌をその手牌の期待値とします。以下が擬似コードです。

def draw(hand):
    # 手牌 hand で現在の巡目が 1 ~ 17 巡目のときの期待値
    exp_values = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

    # 手牌 hand の有効牌一覧を取得する
    draw_tiles = get_draw_tiles(hand)

    for tile in draw_tiles:
        # 手牌に tile を追加する。
        add_tile(hand, tile)

        # 除いた手牌の期待値
        if 和了の場合:
            # 摸して14枚になった手牌の点数を計算する
            score = get_score(hand)
        else:
            # 自摸して14枚になった手牌の期待値を計算する。
            next_exp_values = discard(hand)

        for i = 1 to 17:
            # 手牌 hand の i 巡目の期待値
            for j = i + 1 to 17:
                # 手牌 hand の i 巡目の場合に、j 巡目に有効牌 tile を自摸する確率は
                # 「j 巡目に有効牌 tile を自摸する確率」 * 「i + 1 ~ j 巡目までにいずれの有効牌も引けなかった確率」

                # j 巡目に有効牌 tile を自摸する確率
                tumo_prob = 「牌 tile の残り枚数」/「j + 1 巡目の残り牌の合計枚数」
                if j != i + 1:
                    # i + 1 ~ j - 1 巡目までにいずれの有効牌も引けなかった確率
                    for k = i + 1 to j - 1:
                        tumo_prob *= 「k 巡目の残り牌の合計枚数 - 有効牌の合計枚数」/ 「k 巡目の残り牌の合計枚数」

                if 和了の場合:
                    exp_values[i] += tumo_prob * score
                elif 和了でない かつ自摸回数が残っている場合:
                    exp_values[i] += tump_prob * next_exp_values[j + 1]

        # 手牌に追加した tile を戻す
        remove_tile(hand, tile)

    return exp_values

高速化

探索過程で同じ手牌が現れることがあります。期待値を計算済みの手牌はキャッシュしておき、2回目以降はキャッシュを参照することで計算時間を大幅に短縮できます。

参考資料

• あらの（一人）麻雀研究所: 期待値以外にも麻雀の様々な事柄について解析されており、非常に参考になります。