概要
scikit-learn を使った特徴量のスケーリング方法について解説します。
データ行列
サンプル数を $m$、特徴量の次元数を $n$ としたとき、データセットは $(m, n)$ の2次元配列で表されます。
特徴量のスケーリングは、特徴量の特徴ごと (列ごと) に行います。
StandardScaler
sklearn.preprocessing.StandardScaler は特徴の平均を0、分散を1となるように変換します。この変換を標準化といいます。
データセットを $\mathbf{x}_1, \mathbf{x}_2, \cdots, \mathbf{x}_m \in \mathbb{R}^n$ としたとき、スケーリング後の値 $x’_{ij}$ は
$$ \begin{aligned} x’_{ij} &= \frac{x_{ij} – \mu_j}{\sigma_j} \\ \mu_j &= \frac{1}{N} \sum_{i=0}^m x_{ij} \quad \because 平均\\ \sigma_j &= \sqrt{\frac{1}{N} \sum_{i=0}^m (x_{ij} – \mu_j)^2} \quad \because 標準偏差 \end{aligned} $$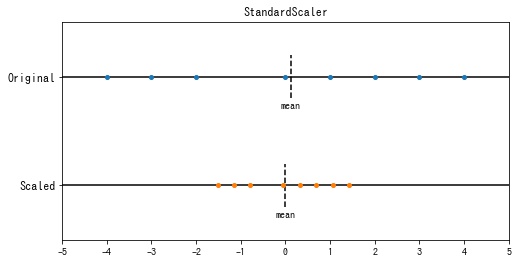
import numpy as np
from sklearn.preprocessing import StandardScaler
# データセットを作成する。(サンプル数, 特徴量の次元数) の2次元配列で表される。
np.random.seed(seed=1)
X = np.random.multivariate_normal([5, 5], [[5, 0], [0, 2]], 50)
# 変換器を作成する。
transformer = StandardScaler()
# 変換する。
X_scaled = transformer.fit_transform(X)
for i, f in enumerate(X_scaled.T):
print(f"feature: {i}, mean: {f.mean():.2f}, std: {f.std():.2f}")feature: 0, mean: -0.00, std: 1.00 feature: 1, mean: -0.00, std: 1.00
特徴ごとに平均が0、分散が1となっていることが確認できます。
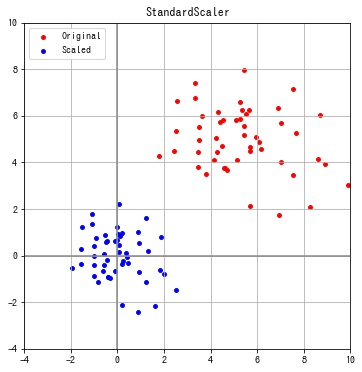
MinMaxScaler
sklearn.preprocessing.MinMaxScaler は各特徴の値の範囲が $[0, 1]$ となるように変換します。この変換を正規化といいます。
データセットを $\mathbf{x}_1, \mathbf{x}_2, \cdots, \mathbf{x}_m \in \mathbb{R}^n$ としたとき、スケーリング後の値 $x’_{ij}$ は
$$ \begin{aligned} x’_{ij} =& \frac{x_{ij} – \displaystyle\min_j x_{ij}}{\displaystyle\max_j x_{ij} – \displaystyle\min_j x_{ij}} \end{aligned} $$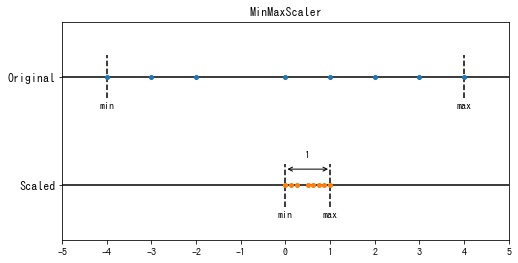
from sklearn.preprocessing import MinMaxScaler
# (サンプル数, 特徴量の次元数) の2次元配列で表されるデータセットを作成する。
np.random.seed(seed=1)
X = np.random.multivariate_normal([1.5, 1.2], [[3, 0], [0, 2]], 50)
# 変換器を作成する。
transformer = MinMaxScaler()
# 変換する。
X_scaled = transformer.fit_transform(X)
for i, f in enumerate(X_scaled.T):
print(f"feature: {i}, min: {f.min():.2f}, max: {f.max():.2f}")feature: 0, min: 0.00, max: 1.00 feature: 1, min: 0.00, max: 1.00
特徴ごとに最小値が0、最大値が1となっていることが確認できます。
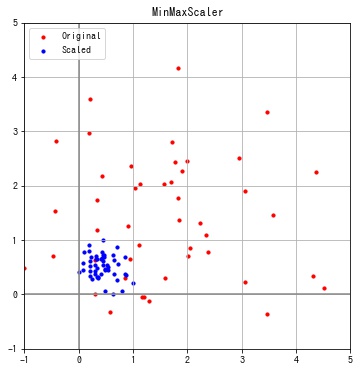
MaxAbsScaler
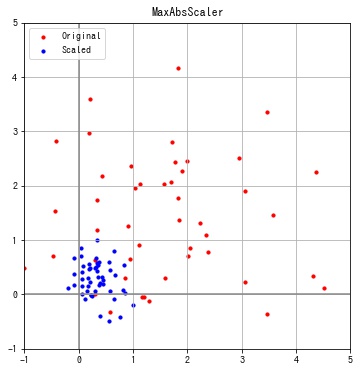
sklearn.preprocessing.MaxAbsScaler は各特徴の最大値が1となるように変換します。
データセットを $\mathbf{x}_1, \mathbf{x}_2, \cdots, \mathbf{x}_m \in \mathbb{R}^n$ としたとき、スケーリング後の値 $x’_{ij}$ は
$$ x’_{ij} = \frac{x_{ij}}{|\displaystyle\max_j x_{ij}|} $$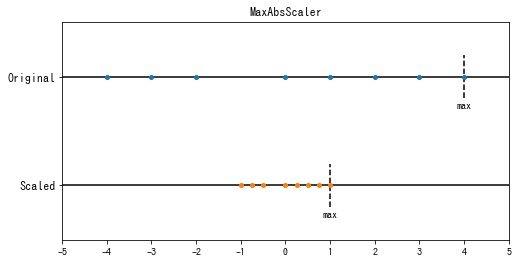
from sklearn.preprocessing import MaxAbsScaler
# (サンプル数, 特徴量の次元数) の2次元配列で表されるデータセットを作成する。
np.random.seed(seed=1)
X = np.random.multivariate_normal([5, 5], [[5, 0], [0, 2]], 50)
# 変換器を作成する。
transformer = MaxAbsScaler()
# 変換する。
X_scaled = transformer.fit_transform(X)
for i, f in enumerate(X_scaled.T):
print(f'feature: {i}, max: {np.abs(f.max()):.2f}')feature: 0,max: 1.00 feature: 1,max: 1.00
特徴ごとに最大値の絶対値が1となっていることが確認できます。
RobustScaler
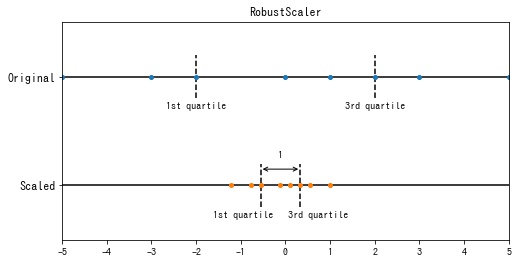
sklearn.preprocessing.RobustScaler は各特徴の第1分位点 $Q_1$ と第3分位点 $Q_3$ の範囲 $[Q_1, Q_3]$ が1になるように変換します。
データセットを $\mathbf{x}_1, \mathbf{x}_2, \cdots, \mathbf{x}_m \in \mathbb{R}^n$ としたとき、スケーリング後の値 $x’_{ij}$ は
$$ x’_{ij} = \frac{x_{ij} – Q_1^{(j)}}{Q_3^{(j)} – Q_1^{(j)}} $$- $Q_1^{(j)}$: 特徴 $j$ の第1分位点
- $Q_3^{(j)}$: 特徴 $j$ の第3分位点
from sklearn.preprocessing import RobustScaler
# (サンプル数, 特徴量の次元数) の2次元配列で表されるデータセットを作成する。
np.random.seed(seed=1)
X = np.random.multivariate_normal([5, 5], [[5, 0], [0, 2]], 50)
# 変換器を作成する。
transformer = RobustScaler()
# 変換する。
X_scaled = transformer.fit_transform(X)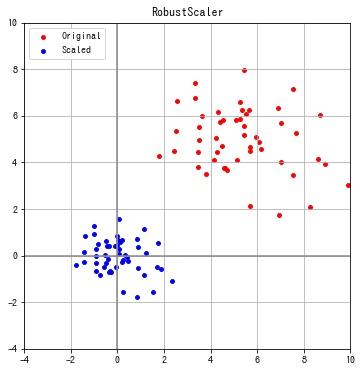


コメント