OpenCV – 画像に適用するアフィン変換について

2020.06.14
OpenCV
OpenCV, 画像処理

1. 概要
2. アフィン変換
- 2.1. 標準座標系と画像座標系
- 2.2. 画像座標系のアフィン変換行列を求める方法
3. 画像にアフィン変換を適用する
4. アフィン変換の種類

概要

画像に対して適用するアフィン変換について解説します。 OpenCV で画像にアフィン変換を適用する方法については、OpenCV – warpAffine でアフィン変換を行う方法についてを参照してください。

アフィン変換

アフィン変換 は、線型変換と平行移動の組み合わせで表される変換です。回転、平行移動、せん断、反転などはアフィン変換の一種です。画像のように2次元の場合、アフィン変換は線形変換を表す行列 $A \in \mathbb{R}^{2 \times 2}$ と平行移動を表すベクトル $\mathbf{t} \in \mathbb{R}^2$ によって表されます。

$$ A = \begin{pmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{pmatrix}, \mathbf{t} = \begin{pmatrix} t_1\\ t_2 \end{pmatrix} $$

変換前の点を $\mathbf{x} = (x_1, x_2)^T$、アフィン変換後の点 $\mathbf{y} = (y_1, y_2)^T$ は次の式で計算できます。

$$ \mathbf{y} = A \mathbf{x} + \mathbf{t} = \begin{pmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{pmatrix} \begin{pmatrix} x_1\\ x_2 \end{pmatrix} + \begin{pmatrix} t_1\\ t_2 \end{pmatrix} $$

ここで、同次座標系を導入すると、アフィン変換は (3, 3) の1つの行列で表すことができ、行列積で計算できるようになります。 $\mathbf{x}, \mathbf{y}$ は同次座標系でそれぞれ $\mathbf{x}’ = (x_1, x_2, 1)^T, \mathbf{y}’ = (y_1, y_2, 1)^T$ となり、先程の計算は以下のようになります。

$$ \begin{pmatrix} y_1\\ y_2\\ 1 \end{pmatrix} = \begin{pmatrix} a_{11} & a_{12} & t_1\\ a_{21} & a_{22} & t_2\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x_1\\ x_2\\ 1 \end{pmatrix} $$

標準座標系と画像座標系

数学では2次元の場合、通常は右方向に $x$ 軸、上方向に $y$ 軸をとる標準座標系 (standard coordinate system) が用いられます。一方、画像処理では、画像の左上を原点とし、右方向に $x$ 軸、下方向に $y$ 軸をとる画像座標系 (image coordinate system) が用いられます。

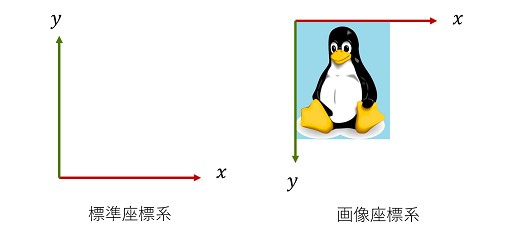
標準座標系での変換行列は画像座標系では異なる場合があります。

画像座標系のアフィン変換行列を求める方法

標準座標系でのアフィン変換行列がわかっている場合に、それを画像座標系でのアフィン変換行列に変換する方法について述べます。

標準座標系の基底 $\mathbf{e}_1 = (1, 0)^T, \mathbf{e}_2 = (0, 1)^T$ を画像座標系の基底 $\mathbf{e}’_1 = (1, 0)^T, \mathbf{e}’_2 = (0, -1)^T$ に変換する基底変換行列は

$$ P = \begin{pmatrix} 1 & 0 \\ 0 & -1 \\ \end{pmatrix} $$

なので、標準座標系での変換行列を $A$ としたとき、$P^{-1} = P$ に注意すると、画像座標系での変換行列は $PAP$ を計算することで求められます。

例:

標準座標系で原点を中心に反時計回りに $\theta$ だけ回転する行列は以下になります。

$$ A = \begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \\ \end{pmatrix} $$

このとき、画像座標系での変換行列は

$$ P^{-1}AP = \begin{pmatrix} \cos \theta & \sin \theta \\ \sin (-\theta) & \cos \theta \\ \end{pmatrix} $$

となります。$A_{21}$ が標準座標系と異なっています。

画像にアフィン変換を適用する

本項では、画像にアフィン変換を適用する方法について、numpy で実装しながら理解します。

In [1]:

import cv2
import numpy as np
from IPython.display import Image, display


def imshow(img):
    """ndarray 配列をインラインで Notebook 上に表示する。
    """
    ret, encoded = cv2.imencode(".jpg", img)
    display(Image(encoded))

画像を $x$ 方向に $s_x$ 倍、$y$ 方向に $s_y$ 倍だけスケールするアフィン変換は以下になります。

$$ A = \begin{pmatrix} s_x & 0 \\ 0 & s_y \\ \end{pmatrix} $$

このアフィン変換行列を同時座標系で作成します。

In [2]:

def scale_matrix(sx, sy):
    A = np.array([[sx, 0, 0],
                  [0, sy, 0],
                  [0, 0, 1]], dtype=float)
    return A


A = scale_matrix(sx=2, sy=2)
print(A)

[[2. 0. 0.]
 [0. 2. 0.]
 [0. 0. 1.]]

画像にアフィン変換する方法として、まず素朴に画像の各画素の座標一覧を作成し、それにアフィン変換を適用する方法を考えます。

In [3]:

# 画像を読み込む。
img = cv2.imread("sample.jpg")
h, w = img.shape[:2]


def make_grid(w, h):
    X, Y = np.indices((w, h)).reshape(2, -1)
    coords = np.vstack((X, Y, np.ones_like(X)))

    return coords


# 画像の各画素の座標一覧を作成する。
src_coords = make_grid(w, h)
src_xs, src_ys, _ = src_coords

行列 A を画像の各画素の座標一覧 src_coords に乗算し、アフィン変換後の各画素の座標一覧 dst_coords を計算します。座標は float になっているので、numpy.round() で整数に丸めて、ndarray.astype(np.int) で整数型にします。変換したあとに出力画像の範囲内 $x \in [0, w – 1], y \in [0, y – 1]$ に収まっている座標のみを抽出します。

In [4]:

# 入力画像の各画素の座標一覧に対して、アフィン変換を行い、変換後の各画素の座標一覧を求める。
dst_coords = np.round(A @ src_coords).astype(np.int)
dst_xs, dst_ys, _ = dst_coords

# 出力画像の範囲内に収まっているインデックスを調べる。
indices = np.where((0 <= dst_xs) & (dst_xs < w) & (0 <= dst_ys) & (dst_ys < h))
src_xs, src_ys = src_xs[indices], src_ys[indices]
dst_xs, dst_ys = dst_xs[indices], dst_ys[indices]

以上で入力画像の座標とアフィン変換後の座標の対応関係が求められました。まず、numpy.zeros_like(img) で真っ黒の画像を作成し、求めた対応関係に基づき、出力画像の画素に入力画像の画素を代入します。

In [5]:

# 出力画像を作成する。
out = np.zeros_like(img)
out[dst_ys, dst_xs] = img[src_ys, src_xs]

imshow(out)

結果を見ると、たしかに $x$ 方向に 2 倍、$y$ 方向に 2 倍されているようですが、色がない点が目立ちます。この現象は、入力画像の画素と対応関係ない出力画像の画素が生じるため、その結果、入力画像の画素が代入されず、黒色のままになってしまうのが原因です。

これを防ぐために、逆に出力画像の各画素の座標一覧を作成し、逆のアフィン変換を行い、変換前の各画素の座標一覧を求めるようにします。逆のアフィン変換行列は、元の行列の逆行列になります。逆行列は numpy.linalg.inv() で求められます。

In [6]:

# 出力画像の各画素の座標一覧を作成する。
dst_coords = make_grid(w, h)
dst_xs, dst_ys, _ = dst_coords

# 出力画像の各画素の座標一覧に対して、逆のアフィン変換を行い、変換前の各画素の座標一覧を求める。
inv_A = np.linalg.inv(A)
src_coords = np.round(inv_A @ dst_coords).astype(np.int)
src_xs, src_ys, _ = src_coords

# 入力画像の範囲内に収まっているインデックスを調べる。
indices = np.where((0 <= src_xs) & (src_xs < w) & (0 <= src_ys) & (src_ys < h))
src_xs, src_ys = src_xs[indices], src_ys[indices]
dst_xs, dst_ys = dst_xs[indices], dst_ys[indices]

# 出力画像を作成する。
out = np.zeros_like(img)
out[dst_ys, dst_xs] = img[src_ys, src_xs]

imshow(out)

今度は、すべての画素に色がつきました。

アフィン変換の種類

代表的なアフィン変換の種類を紹介します。

拡大縮小

$x$ 軸方向に $s_x$、$y$ 軸方向に $s_y$ だけ拡大縮小 (scaling) するアフィン変換行列です。

標準座標系	画像座標系
$$\begin{pmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}$$	$$\begin{pmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}$$

例: $x$ 軸方向に1.2倍、$y$ 軸方向に0.8倍する変換

回転

原点を中心に反時計回りに $\theta$ だけ回転 (rotation) するアフィン変換行列です。

標準座標系	画像座標系
$\begin{pmatrix} \cos \theta & -\sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}$	$\begin{pmatrix} \cos \theta & \sin \theta & 0 \\ \sin (-\theta) & \cos \theta & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}$

例: 原点を中心に反時計回りに30°回転する変換

平行移動

$x$ 軸方向に $t_x$、$y$ 軸方向に $t_y$ だけ平行移動 (translation) するアフィン変換行列です。

標準座標系	画像座標系
$\begin{pmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \\ \end{pmatrix}$	$\begin{pmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \\ \end{pmatrix}$

例: $x$ 軸方向に 60、$y$ 軸方向に 30 だけ平行移動する変換

反転

$x$ 軸に対して反転するアフィン変換行列です。

標準座標系	画像座標系
$\begin{pmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}$	$\begin{pmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}$

$y$ 軸に対して反転するアフィン変換行列です。

標準座標系	画像座標系
$\begin{pmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}$	$\begin{pmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}$

せん断

水平せん断 (sheer) するアフィン変換行列です。

標準座標系	画像座標系
$\begin{pmatrix} 1 & \lambda & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}$	$\begin{pmatrix} 1 & -\lambda & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}$

鉛直せん断 (sheer) するアフィン変換行列です。

標準座標系	画像座標系
$\begin{pmatrix} 1 & 0 & 0 \\ \lambda & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}$	$\begin{pmatrix} 1 & 0 & 0 \\ -\lambda & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}$

前の記事

OpenCV – VideoCapture、VideoWriter の使い方 2020.06.10
次の記事

OpenCV – warpAffine でアフィン変換を行う方法について 2020.06.14