概要
画像処理における画像のモーメントについて解説し、OpenCV を使用したコードについて紹介します。
モーメント
関数のモーメント (Moments) は、関数の形状に関連した指標です。
関数 $f(x, y)$ の(原点周りの) $n$ 次のモーメント (n-th order Moment/n-th Order Raw Moment)** は、次のように表されます。
$$ M_{pq} = \int^\infty_{-\infty} \int^\infty_{-\infty} x^p y^q f(x, y) dx dy $$ただし、$n = p + q, p, q \in \mathbb{Z}_+$ です。
また、関数 $f(x, y)$ の $c = (c_x, c_y)$ 周りの $n$ 次のモーメント (n-th order Moment about c)** は、次のように表されます。
$$ M_{pq} = \int^\infty_{-\infty} \int^\infty_{-\infty} (x – c_x)^p (y – c_y)^q f(x, y) dx dy $$画像モーメント
画像の位置 $x, y$ の画素値を $I(x, y)$ としたとき、$I(x, y)$ のモーメントを画像モーメント (Image Moment) といいます。
$n$ 次のモーメント (n-th order Moment/n-th Order Raw Moment)** は、次のように表されます。
$$ M_{pq} = \sum_{x, y} x^p y^q I(x, y) $$ただし、$n = p + q, p, q \in \mathbb{Z}_+$ です。
また、$c = (c_x, c_y)$ 周りの $n$ 次のモーメント (n-th order Moment about c)** は、次のように表されます。
$$ M_{pq} = \sum_{x, y} (x – c_x)^p (y – c_y)^q I(x, y) $$ここで、$c$ を重心 $(\bar{x}, \bar{y})$ としたとき、このモーメントを $n$ 次の中心モーメント (n-th order Central Moment) といいます。中心モーメントは次のように表されます
$$ M_{pq} = \sum_{x, y} (x – \bar{x})^p (y – \bar{y})^q I(x, y) $$原点周りのモーメント
3 次までの原点周りのモーメントは以下のようになります。
$$ \begin {aligned} M_{00} &= \sum_{x, y} I(x, y) \quad \because \text{0次モーメント} \\ M_{10} &= \sum_{x, y} x I(x, y) \quad \because \text{1次モーメント} \\ M_{01} &= \sum_{x, y} y I(x, y) \quad \because \text{1次モーメント} \\ M_{20} &= \sum_{x, y} x^2 I(x, y) \quad \because \text{2次モーメント} \\ M_{11} &= \sum_{x, y} x y I(x, y) \quad \because \text{2次モーメント} \\ M_{02} &= \sum_{x, y} y^2 I(x, y) \quad \because \text{2次モーメント} \\ M_{30} &= \sum_{x, y} x^3 I(x, y) \quad \because \text{3次モーメント} \\ M_{21} &= \sum_{x, y} x^2 y I(x, y) \quad \because \text{3次モーメント} \\ M_{12} &= \sum_{x, y} x y^2 I(x, y) \quad \because \text{3次モーメント} \\ M_{03} &= \sum_{x, y} y^3 I(x, y) \quad \because \text{3次モーメント} \\ \end {aligned} $$原点周りのモーメントを計算する
import cv2
import numpy as np
from IPython.display import Image, display
def imshow(img):
"""ndarray 配列をインラインで Notebook 上に表示する。"""
ret, encoded = cv2.imencode(".jpg", img)
display(Image(encoded))以下のように計算できます。
def raw_moment(img, i, j):
x = np.arange(img.shape[1]) ** i
y = np.arange(img.shape[0]) ** j
XX, YY = np.meshgrid(x, y)
return (XX * YY * img).sum()
# 画像を読み込む。
img = cv2.imread("sample.png", cv2.IMREAD_GRAYSCALE)
print(f"M_00: {raw_moment(img, 0, 0)}")
print(f"M_10: {raw_moment(img, 1, 0)}")
print(f"M_01: {raw_moment(img, 0, 1)}")
print(f"M_20: {raw_moment(img, 2, 0)}")
print(f"M_11: {raw_moment(img, 1, 1)}")
print(f"M_02: {raw_moment(img, 0, 2)}")
print(f"M_30: {raw_moment(img, 3, 0)}")
print(f"M_21: {raw_moment(img, 2, 1)}")
print(f"M_12: {raw_moment(img, 1, 2)}")
print(f"M_03: {raw_moment(img, 0, 3)}")M_00: 2845545 M_10: 426890145 M_01: 426889635 M_20: 66715214715 M_11: 63176372145 M_02: 66711513645 M_30: 10810531774515 M_21: 9748900563255 M_12: 9748388424825 M_03: 10808910214215
OpenCV では、cv2.moments() を使用して画像モーメントを計算できます。原点周りのモーメントは、返り値の辞書に mij という名前で格納されています。
# 画像を読み込む。
img = cv2.imread("sample.png", cv2.IMREAD_GRAYSCALE)
# モーメントを計算する
M = cv2.moments(img)
print(f"M_00: {M['m00']}")
print(f"M_10: {M['m10']}")
print(f"M_01: {M['m01']}")
print(f"M_20: {M['m20']}")
print(f"M_11: {M['m11']}")
print(f"M_02: {M['m02']}")
print(f"M_30: {M['m30']}")
print(f"M_21: {M['m21']}")
print(f"M_12: {M['m12']}")
print(f"M_03: {M['m03']}")M_00: 2845545.0 M_10: 426890145.0 M_01: 426889635.0 M_20: 66715214715.0 M_11: 63176372145.0 M_02: 66711513645.0 M_30: 10810531774515.0 M_21: 9748900563255.0 M_12: 9748388424825.0 M_03: 10808910214215.0
面積を計算する
値が $0,1$ の 2 値画像の場合、$M_{00}$ は値が 1 の画素数になるため、面積を表します。
$$ M_{00} = \sum_{x, y} I(x, y) = \text{Area} $$グレースケール画像の場合、$M_{00}$ は輝度値の合計になります。
$$ M_{00} = \sum_{x, y} I(x, y) = \text{Sum of Gray Level} $$# 画像を読み込む。
img = cv2.imread("sample.png", cv2.IMREAD_GRAYSCALE)
# モーメントを計算する
M = cv2.moments(img)
# 今回の場合、0でない値は255なので、255で割ると、面積になる
area = M["m00"] / 255
print(f"area: ({area:.2f})")area: (11159.00)
重心を計算する
$$ \begin {aligned} E[X – \bar{x}] &= 0 \\ E[Y – \bar{y}] &= 0 \end {aligned} $$を満たす点 $\bar{x}, \bar{y}$ を重心といいます。
$$ \begin {aligned} E[X – \bar{x}] &= \sum_{x, y} (x – \bar{x}) I(x, y) \\ &= \sum_{x, y} x I(x, y) – \bar{x} \sum_{x, y} I(x, y) \\ &= M_{10} – \bar{x} M_{00} \\ &= 0 \end {aligned} $$より、$\bar{x} = \frac{M_{10}}{M_{00}}$ と求まります。 $\bar{y}$ も同様に、$\bar{y} = \frac{M_{01}}{M_{00}}$ となります。
# 画像を読み込む。
img = cv2.imread("sample.png", cv2.IMREAD_GRAYSCALE)
# モーメントを計算する
M = cv2.moments(img)
# 重心を計算する。
cx = M["m10"] / M["m00"]
cy = M["m01"] / M["m00"]
print(f"centroid: ({cx:.2f}, {cy:.2f})")
# 描画する。
color = cv2.cvtColor(img, cv2.COLOR_GRAY2BGR)
cv2.circle(color, (int(cx), int(cy)), 5, (0, 255, 0), thickness=-1)
imshow(color)centroid: (150.02, 150.02)
中心モーメント
$$ \mu_{pq} = \sum_{x, y} (x_p – \bar{x})^p (y_p – \bar{y})^q I(x, y) $$を $n$ 次の中心モーメント (n-th order Center Moment)といいます。 ただし、$(\bar{x}, \bar{y})$ は重心であり、$\bar{x} = \frac{M_{10}}{M_{00}}, \bar{y} = \frac{M_{01}}{M_{00}}$ です。
0 次の中心モーメント
0 次の中心モーメントは、原点回りの 0 次のモーメントと一致します。
$$ \mu_{00} = \sum_{x, y} I(x, y) = M_{00} $$1 次の中心モーメント
1 次の中心モーメントは 0 になります。
$$ \begin {aligned} \mu_{10} &= \sum_{x, y} (x – \bar{x}) I(x, y) \\ &= \sum_{x, y} x I(x, y) – \bar{x} \sum_{x, y} I(x, y) \\ &= M_{10} – \frac{M_{10}}{M_{00}} M_{00} \\ &= 0 \\ \end {aligned} $$$$ \begin {aligned} \mu_{01} &= \sum_{x, y} (y – \bar{y}) I(x, y) \\ &= \sum_{x, y} y I(x, y) – \bar{y} \sum_{x, y} I(x, y) \\ &= M_{01} – \frac{M_{01}}{M_{00}} M_{00} \\ &= 0 \\ \end {aligned} $$2 次の中心モーメント
$$ \begin{aligned} \mu_{20} &= \sum_{x, y} (x – \bar{x})^2 I(x, y) \\ &= \sum_{x, y} x^2 I(x, y) – 2 \bar{x} \sum_{x, y} x I(x, y) + \bar{x}^2 \sum_{x, y} I(x, y) \\ &= M_{20} – 2 \frac{M_{10}}{M_{00}} M_{10} + \frac{M_{10}^2}{M_{00}^2} M_{00} \\ &= M_{20} – \frac{M_{10}^2}{M_{00}} \\ &= M_{20} – \bar{x} M_{10} \\ \mu_{11} &= \sum_{x, y} (x – \bar{x})(y – \bar{y}) I(x, y) \\ &= \sum_{x, y} xy I(x, y) – \bar{y} \sum_{x, y} x I(x, y) – \bar{x} \sum_{x, y} y I(x, y) + \bar{x} \bar{y} \sum_{x, y} I(x, y) \\ &= M_{11} – \frac{M_{01}}{M_{00}} M_{10} – \frac{M_{10}}{M_{00}} M_{01} + \frac{M_{10}}{M_{00}} \frac{M_{01}}{M_{00}} M_{00} \\ &= M_{11} – \frac{M_{10}M_{01}}{M_{00}} \\ &= M_{11} – \bar{y} M_{10} = M_{11} – \bar{x} M_{01} \\ \mu_{02} &= \sum_{x, y} (y – \bar{y})^2 I(x, y) \\ &= \sum_{x, y} y^2 I(x, y) – 2 \bar{y} \sum_{x, y} y I(x, y) + \bar{y}^2 \sum_{x, y} I(x, y) \\ &= M_{02} – 2 \frac{M_{01}}{M_{00}} M_{01} + \frac{M_{01}^2}{M_{00}^2} M_{00} \\ &= M_{02} – \frac{M_{01}^2}{M_{00}} \\ &= M_{02} – \bar{y} M_{01} \\ \end{aligned} $$3 次の中心モーメント
$$ \begin {aligned} \mu_{30} &= \sum_{x, y} (x – \bar{x})^3 I(x, y) \\ &= \sum_{x, y} x^3 I(x, y) – 3 \bar{x} \sum_{x, y} x^2 I(x, y) + 3 \bar{x}^2 \sum_{x, y} x I(x, y) – \bar{x}^3 \sum_{x, y} I(x, y) \\ &= M_{30} – 3 \bar{x} M_{20} + 3 \bar{x} M_{10} – \bar{x}^3 M_{00} \\ &= M_{30} – 3 \bar{x} M_{20} + 3 \frac{M_{10}^2}{M_{00}^2} M_{10} – \frac{M_{10}^3}{M_{00}^3} M_{00} \\ &= M_{30} – 3 \bar{x} M_{20} + 2 \bar{x}^2 M_{10} \\ \mu_{21} &= \sum_{x, y} (x – \bar{x})^2 (y – \bar{y}) I(x, y) \\ &= \sum_{x, y} x^2 y I(x, y) – 2 \bar{x} \sum_{x, y} x y I(x, y) + \bar{x}^2 \sum_{x, y} y I(x, y) \\ &\quad – \bar{y} \sum_{x, y} x^2 I(x, y) + 2 \bar{x} \bar{y} \sum_{x, y} x I(x, y) – \bar{x}^2 \bar{y} \sum_{x, y} I(x, y) \\ &= M_{21} – 2 \bar{x} M_{11} + \bar{x}^2 M_{01} – \bar{y} M_{20} + 2 \bar{x} \bar{y} M_{10} – \bar{x}^2 \bar{y} M_{00} \\ &= M_{21} – 2 \bar{x} M_{11} + 2 \bar{x}^2 M_{01} – \bar{y} M_{20} \\ \mu_{12} &= \sum_{x, y} (x – \bar{x}) (y – \bar{y})^2 I(x, y) \\ &= \sum_{x, y} x y^2 I(x, y) – 2 \bar{y} \sum_{x, y} x y I(x, y) + \bar{y}^2 \sum_{x, y} x I(x, y) \\ &\quad – \bar{x} \sum_{x, y} y^2 I(x, y) + 2 \bar{x} \bar{y} \sum_{x, y} y I(x, y) – \bar{x} \bar{y}^2 \sum_{x, y} I(x, y) \\ &= M_{12} – 2 \bar{y} M_{11} + \bar{y}^2 M_{10} – \bar{x} M_{02} + 2 \bar{x} \bar{y} M_{01} – \bar{x} \bar{y}^2 M_{00} \\ &= M_{12} – 2 \bar{y} M_{11} + 2 \bar{y}^2 M_{10} – \bar{x} M_{02} \\ \mu_{03} &= \sum_{x, y} (y – \bar{y})^3 I(x, y) \\ &= \sum_{x, y} y^3 I(x, y) – 3 \bar{y} \sum_{x, y} y^2 I(x, y) + 3 \bar{y}^2 \sum_{x, y} y I(x, y) – \bar{y}^3 \sum_{x, y} I(x, y) \\ &= M_{03} – 3 \bar{y} M_{02} + 3 \bar{y} M_{01} – \bar{y}^3 M_{00} \\ &= M_{03} – 3 \bar{y} M_{02} + 3 \frac{M_{01}^2}{M_{00}^2} M_{10} – \frac{M_{01}^3}{M_{00}^3} M_{00} \\ &= M_{03} – 3 \bar{y} M_{02} + 2 \bar{y}^2 M_{01} \end {aligned} $$以下のように計算できます。
def center_moment(img, i, j, cx, cy):
x = (np.arange(img.shape[1]) - cx) ** i
y = (np.arange(img.shape[0]) - cy) ** j
XX, YY = np.meshgrid(x, y)
return (XX * YY * img).sum()
# 画像を読み込む。
img = cv2.imread("sample.png", cv2.IMREAD_GRAYSCALE)
cx = M["m10"] / M["m00"]
cy = M["m01"] / M["m00"]
print(f"mu_00: {center_moment(img, 0, 0, cx, cy)}")
print(f"mu_10: {center_moment(img, 1, 0, cx, cy)}")
print(f"mu_01: {center_moment(img, 0, 1, cx, cy)}")
print(f"mu_20: {center_moment(img, 2, 0, cx, cy)}")
print(f"mu_11: {center_moment(img, 1, 1, cx, cy)}")
print(f"mu_02: {center_moment(img, 0, 2, cx, cy)}")
print(f"mu_30: {center_moment(img, 3, 0, cx, cy)}")
print(f"mu_21: {center_moment(img, 2, 1, cx, cy)}")
print(f"mu_12: {center_moment(img, 1, 2, cx, cy)}")
print(f"mu_03: {center_moment(img, 0, 3, cx, cy)}")mu_00: 2845545.0 mu_10: -7.450580596923828e-09 mu_01: -1.862645149230957e-08 mu_20: 2672932516.6439643 mu_11: -865833542.8900439 mu_02: 2669384467.484542 mu_30: -108992931.37587357 mu_21: 46812816.124513626 mu_12: 77643272.30863953 mu_03: -97843014.76109314
OpenCV では、cv2.moments() を使用して画像モーメントを計算できます。中心モーメントは、返り値の辞書に muij という名前で格納されています。ただし、$\mu_{00} = M_{00}$ および $\mu_{10} = \mu_{01} = 0$ のため、これら 3 つのキーは存在しません。
# 画像を読み込む。
img = cv2.imread("sample.png", cv2.IMREAD_GRAYSCALE)
# モーメントを計算する
M = cv2.moments(img)
print(f"M_20: {M['mu20']}")
print(f"M_11: {M['mu11']}")
print(f"M_02: {M['mu02']}")
print(f"M_30: {M['mu30']}")
print(f"M_21: {M['mu21']}")
print(f"M_12: {M['mu12']}")
print(f"M_03: {M['mu03']}")M_20: 2672932516.6439624 M_11: -865833542.8900461 M_02: 2669384467.4845376 M_30: -108992931.37457179 M_21: 46812816.124556035 M_12: 77643272.30957282 M_03: -97843014.75978112
分散共分散行列
$I(x, y)$ を $\sum_{x, y} I(x, y) = \mu_{00} = M_{00}$ で割って総和が 1 となるように規格化すると、確率質量関数として分散共分散行列を考えることができます。
$$ \begin {aligned} \mu_{20}’ &= \sum_{x, y} (x – \bar{x})^2 \frac{I(x, y)}{\mu_{00}} = \frac{\mu_{20}}{\mu_{00}} = \frac{1}{M_{00}}(M_{20} – \bar{x} M_{10}) = \frac{M_{20}}{M_{00}} – \bar{x}^2 \\ \mu_{02}’ &= \sum_{x, y} (y – \bar{y})^2 \frac{I(x, y)}{\mu_{00}} = \frac{\mu_{02}}{\mu_{00}} = \frac{1}{M_{00}}(M_{02} – \bar{y} M_{01}) = \frac{M_{02}}{M_{00}} – \bar{y}^2 \\ \mu_{11}’ &= \sum_{x, y} (x – \bar{x})(y – \bar{y}) \frac{I(x, y)}{\mu_{00}} = \frac{\mu_{11}}{\mu_{00}} = \frac{1}{M_{00}}(M_{11} – \bar{x} M_{01}) = \frac{M_{11}}{M_{00}} – \bar{x} \bar{y} \\ \end {aligned} $$としたとき、分散共分散行列は次のようになります。
$$ \operatorname{Cov} = \begin{pmatrix} \mu_{20}’ & \mu_{11}’ \\ \mu_{11}’ & \mu_{02}’ \end{pmatrix} $$この分散共分散行列の固有値を求めると、
$$ \begin {aligned} \lambda_i &= \frac{\mu_{20}’ + \mu_{02}’}{2} \pm \frac{\sqrt{(\mu’_{20} + \mu’_{02})^2 – 4 (\mu’_{20} \mu’_{02} – \mu’^2_{11})}}{2} \\ &= \frac{\mu_{20}’ + \mu_{02}’}{2} \pm \frac{\sqrt{4\mu’^2_{11} + (\mu’_{20} – \mu’_{02})^2}}{2} \\ \end {aligned} $$値が大きいほうの固有値に対応する固有ベクトルと最も近い xy 軸との角度を次の式で求められます。
$$ \Theta = \frac{1}{2} \arctan \left( \frac{2 \mu’_{11}}{\mu_{20}’ – \mu_{02}’} \right) $$ただし、$\mu_{20}’ \ne \mu_{02}’$ のとき、成り立ちます。
import numpy as np
# 画像を読み込む。
img = cv2.imread("sample.png", cv2.IMREAD_GRAYSCALE)
# モーメントを計算する
M = cv2.moments(img)
# 重心を計算する。
cx = M["m10"] / M["m00"]
cy = M["m01"] / M["m00"]
print(f"centroid: ({cx:.2f}, {cy:.2f})")
# 固有ベクトルの角度を計算する。
mu20 = M["mu20"] / M["m00"]
mu11 = M["mu11"] / M["m00"]
mu02 = M["mu02"] / M["m00"]
rad = np.arctan(2 * mu11 / (mu20 - mu02)) / 2
deg = np.rad2deg(rad)
print(f"angle: {deg:.2f}")
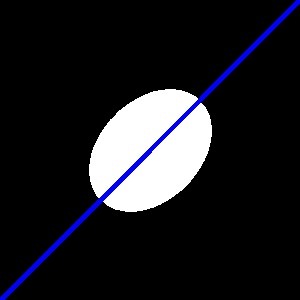
# 描画する。
color = cv2.cvtColor(img, cv2.COLOR_GRAY2BGR)
# y = tanθ (x - cx) + cy
y1 = -cx * np.tan(rad) + cy
y2 = (img.shape[1] - cx) * np.tan(rad) + cy
cv2.line(color, (0, img.shape[1]), (int(y1), int(y2)), (255, 0, 0), thickness=3)
imshow(color)centroid: (150.02, 150.02) angle: -44.94
正規化された中心モーメント
$$ \nu_{ij} = \frac{\mu_{ij}}{M_{00}^{(i + j) / 2 + 1}} $$を正規化された中心モーメントといいます。正規化された中心モーメントはスケーリングに不変な値となります。
$$ \begin {aligned} \nu_{00} &= \frac{\mu_{00}}{M_{00}} = 1 \\ \nu_{10} &= \frac{\mu_{10}}{M_{00}^{3 / 2}} = 0 \\ \nu_{01} &= \frac{\mu_{01}}{M_{00}^{3 / 2}} = 0 \\ \nu_{20} &= \frac{\mu_{20}}{M_{00}^2} \\ \nu_{11} &= \frac{\mu_{11}}{M_{00}^2} \\ \nu_{02} &= \frac{\mu_{02}}{M_{00}^2} \\ \nu_{30} &= \frac{\mu_{30}}{M_{00}^{5 / 2}} \\ \nu_{21} &= \frac{\mu_{21}}{M_{00}^{5 / 2}} \\ \nu_{12} &= \frac{\mu_{12}}{M_{00}^{5 / 2}} \\ \nu_{03} &= \frac{\mu_{03}}{M_{00}^{5 / 2}} \\ \end {aligned} $$Hu モーメント
Hu モーメント (Hu Moment) は、正規化された中心モーメント $\nu_{ij}$ を使用して、回転に対しても不変な次の 7 つの指標のことをいいます。
$$ \begin{aligned} I_{1}&=\nu _{{20}}+\nu _{{02}}\\ I_{2}&=(\nu _{{20}}-\nu _{{02}})^{2}+4\nu _{{11}}^{2}\\ I_{3}&=(\nu _{{30}}-3\nu _{{12}})^{2}+(3\nu _{{21}}-\nu _{{03}})^{2}\\ I_{4}&=(\nu _{{30}}+\nu _{{12}})^{2}+(\nu _{{21}}+\nu _{{03}})^{2}\\ I_{5}&=(\nu _{{30}}-3\nu _{{12}})(\nu _{{30}}+\nu _{{12}})[(\nu _{{30}}+\nu _{{12}})^{2}-3(\nu _{{21}}+\nu _{{03}})^{2}]+(3\nu _{{21}}-\nu _{{03}})(\nu _{{21}}+\nu _{{03}})[3(\nu _{{30}}+\nu _{{12}})^{2}-(\nu _{{21}}+\nu _{{03}})^{2}]\\ I_{6}&=(\nu _{{20}}-\nu _{{02}})[(\nu _{{30}}+\nu _{{12}})^{2}-(\nu _{{21}}+\nu _{{03}})^{2}]+4\nu _{{11}}(\nu _{{30}}+\nu _{{12}})(\nu _{{21}}+\nu _{{03}})\\ I_{7}&=(3\nu _{{21}}-\nu _{{03}})(\nu _{{30}}+\nu _{{12}})[(\nu _{{30}}+\nu _{{12}})^{2}-3(\nu _{{21}}+\nu _{{03}})^{2}]-(\nu _{{30}}-3\nu _{{12}})(\nu _{{21}}+\nu _{{03}})[3(\nu _{{30}}+\nu _{{12}})^{2}-(\nu _{{21}}+\nu _{{03}})^{2}].\\ \end{aligned} $$平行移動、スケーリング、回転した場合のモーメントの変化
サンプルとして次の 4 つの画像を作成し、平行移動、スケーリング、回転した場合の原点周りのモーメント、中心モーメント、正規化された中心モーメントの変化について見てみます。
- img1: 元画像
- img2: img1 を平行移動した画像
- img3: img1 をスケーリングした画像
- img4: img1 を回転した画像
import pandas as pd
img1 = np.zeros((300, 300), dtype=np.uint8)
cv2.ellipse(img1, (150, 150), (50, 70), 45, 0, 360, 255, thickness=-1)
# img1 に平行移動
img2 = np.zeros((300, 300), dtype=np.uint8)
cv2.ellipse(img2, (100, 100), (50, 70), 45, 0, 360, 255, thickness=-1)
# img1 に平行移動、スケーリング
img3 = np.zeros((300, 300), dtype=np.uint8)
cv2.ellipse(img3, (150, 150), (25, 35), 45, 0, 360, 255, thickness=-1)
# img1 に平行移動、スケーリング、回転
img4 = np.zeros((300, 300), dtype=np.uint8)
cv2.ellipse(img4, (150, 150), (50, 70), 120, 0, 360, 255, thickness=-1)
moments = []
for img in [img1, img2, img3, img4]:
imshow(img)
M = cv2.moments(img)
moments.append(M)
moments = pd.DataFrame(moments, index=["img1", "img2", "img3", "img4"])原点周りのモーメントは img1 と img2 を見るとわかるように、平行移動によって値が変化します。
| m00 | m10 | m01 | m20 | m11 | m02 | m30 | m21 | m12 | m03 | |
|---|---|---|---|---|---|---|---|---|---|---|
| img1 | 2845545.0 | 426890145.0 | 426889635.0 | 6.671521e+10 | 6.317637e+10 | 6.671151e+10 | 1.081053e+13 | 9.748901e+12 | 9.748388e+12 | 1.080891e+13 |
| img2 | 2845545.0 | 284612895.0 | 284612385.0 | 3.114006e+10 | 2.760125e+10 | 3.113641e+10 | 3.649233e+12 | 2.941484e+12 | 2.941156e+12 | 3.648162e+12 |
| img3 | 720630.0 | 108079200.0 | 108078435.0 | 1.638041e+10 | 1.615581e+10 | 1.637996e+10 | 2.507956e+12 | 2.440599e+12 | 2.440549e+12 | 2.507806e+12 |
| img4 | 2847075.0 | 427082670.0 | 427123980.0 | 6.717000e+10 | 6.481808e+10 | 6.631872e+10 | 1.100729e+13 | 1.030089e+13 | 1.017229e+13 | 1.062160e+13 |
中心モーメントは img2 を見るとわかるように、平行移動では値が変化しません。
しかし、img2 と img3 を見るとわかるように、スケーリングや回転によって値が変化します。
| mu20 | mu11 | mu02 | mu30 | mu21 | mu12 | mu03 | |
|---|---|---|---|---|---|---|---|
| img1 | 2.672933e+09 | -8.658335e+08 | 2.669384e+09 | -1.089929e+08 | 4.681282e+07 | 7.764327e+07 | -9.784301e+07 |
| img2 | 2.672933e+09 | -8.658335e+08 | 2.669384e+09 | -1.089929e+08 | 4.681282e+07 | 7.764327e+07 | -9.784301e+07 |
| img3 | 1.708242e+08 | -5.365999e+07 | 1.706056e+08 | 2.788358e+06 | -1.557906e+06 | -1.836906e+06 | 2.677462e+06 |
| img4 | 3.104385e+09 | 7.462708e+08 | 2.240709e+09 | -8.202304e+07 | 2.025908e+07 | 6.871483e+07 | 1.806833e+07 |
正規化された中心モーメントは、img2 と img3 を見るとわかるように、平行移動やスケーリングでは値が変化しません。しかし、img4 を見るとわかるように、回転によって値が変化します。
| nu20 | nu11 | nu02 | nu30 | nu21 | nu12 | nu03 | |
|---|---|---|---|---|---|---|---|
| img1 | 0.000330 | -0.000107 | 0.000330 | -7.979666e-09 | 3.427292e-09 | 5.684473e-09 | -7.163350e-09 |
| img2 | 0.000330 | -0.000107 | 0.000330 | -7.979666e-09 | 3.427292e-09 | 5.684473e-09 | -7.163350e-09 |
| img3 | 0.000329 | -0.000103 | 0.000329 | 6.325103e-09 | -3.533951e-09 | -4.166834e-09 | 6.073548e-09 |
| img4 | 0.000383 | 0.000092 | 0.000276 | -5.997062e-09 | 1.481230e-09 | 5.024041e-09 | 1.321054e-09 |










コメント