概要
ディープラーニングの画像認識モデルである ResNeXt を解説し、Pytorch の実装例を紹介します。
ResNet
ResNet は、画像認識のコンテスト ILSVRC 2015 にて、top5 error rate で3.57%を記録し、優勝した CNN ネットワークモデルです。その後、いくつか改良したモデルが出てきて、今回紹介する ResNeXt もその亜種になります。
[blogcard url=”https://pystyle.info/pytorch-resnet”]
ResNeXt
Aggregated Residual Transformations for Deep Neural Networks で紹介された ResNet の改良モデルです。
cardinality の定義
入力数が $D$、出力数が$1$のシンプルなニューロンの計算について考えます。 入力を $\mathbf{x} \in \R^D$、全結合層の重みを $\mathbf{w} \in \R^D$ としたとき、全結合層の計算は
$$ \sum_{i = 1}^D w_i x_i = \mathbf{w} \cdot \mathbf{x} $$で計算できます。
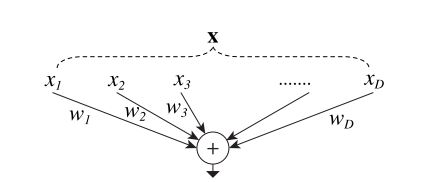
この処理は次の組み合わせとして解釈できます。
- $\mathbf{x}$ を $x_1, x_2, \cdots, x_D$ という低い次元に分割する (分割)
- それぞれ $x_i w_i$ を計算する。(変換)
- すべての変換結果を足し合わせる (集計)
これを一般化すると、
$$ \mathcal{F}(\mathbf{x}) = \sum_{i = 1}^C \mathcal{T}_i (\mathbf{x}) $$$\mathcal{T}_i (\mathbf{x})$ は任意の関数で、必要に応じてより低い次元に次元削減したあと、変換を行います。$C$ は $\mathcal{F}(\mathbf{x})$ を構成する変換の数で、大きいほど複雑な変換を表せます。論文では、$C$ の値を 基数 (cardinality) とよんでいます。
Bottleneck Block を使用した変換
論文では、簡単にするために $\mathcal{T}_i$ はすべて同じ変換とし、これを ResNet の Bottleneck Block にします。Bottleneck Block ブロックの最初の 1×1 の畳み込み層ではチャンネル数が $D$ の入力をより少ないチャンネル数に次元削減します。各 Bottleneck Block の出力を集計し、$\mathcal{F}(\mathbf{x}) = \sum_{i = 1}^C \mathcal{T}_i(\mathbf{x})$ とします。最後に Shortcut Connection と結合し、$\mathcal{F} (\mathbf{x}) + \mathbf{x}$ を出力します。
分割のパラメータについて
Bottleneck の in_channels、out_channels を割り切れる値で分割する必要があります。Bottleneck の in_channels、out_channels がとり得る値は $64, 256, 256, 512, 1024, 2048$ であり、これらの公約数は $1, 2, 4, 8, 16, 32, 64$ です。
次にモデルのパラメータ数は同等に維持しつつ、分割後の畳み込みの出力チャンネル数 $d$ を決めます。
- 通常の Bottleneck のパラメータ数は
in_channels * channels + 3 * 3 * channels * channels + channels * 4 * channelsと計算できます。 - 分割版の Bottleneck のパラメータ数は
C * (in_channels * d + 3 * 3 * d * d + d * 4 * channels)と計算できます。
分割数 C をある値にしたとき、通常の Bottleneck のパラメータ数と変わらないように $d$ を決めるには、この2つが同じ値になる $d$ の値を求めればよいことがわかります。
例えば、in_channels = 256, channels=64 の Bottleneck の場合は次のように求められます。
from sympy import N, solve, symbols
d = symbols("d", real=True, positive=True)
# 通常の Bottleneck のパラメータ数
in_channels = 256
channels = 64
n_params = in_channels * channels + 9 * channels * channels + channels * channels * 4
# C を変化させた場合のパラメータ数を変えない d を求める
for C in [1, 2, 4, 8, 16, 32, 64]:
z = C * (256 * d + 9 * d * d + d * 256)
sol = N(solve(z - n_params, d)[0])
print(f"C={C}, d={sol:.0f}")C=1, d=64 C=2, d=40 C=4, d=24 C=8, d=14 C=16, d=8 C=32, d=4 C=64, d=2
論文では、この $C=1, 2, 4, 8, 32$ に対して、ResNet-50 及び ResNet-101 の分割したバージョンの精度の検証を行いました。 その結果、いずれも $C=32, d=4$ が最もよい精度がでることがわかりました。
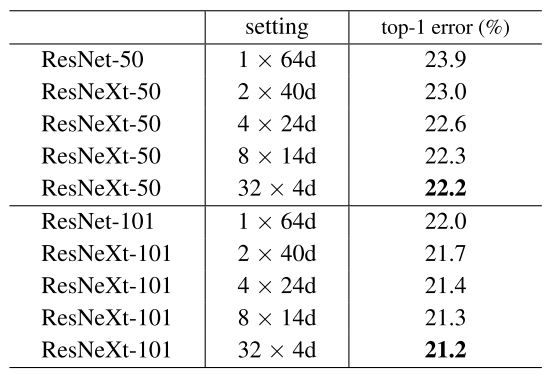
C=32 の場合、各 in_channels, channels の場合において、通常の Bottleneck のパラメータ数と変わらない $d$ を求めると次のようになります。
from sympy import N, solve, symbols
channel_params = [
[64, 64],
[256, 64],
[256, 128],
[512, 128],
[512, 256],
[1024, 256],
[1024, 512],
[2048, 512],
]
C = 32
for in_channels, channels in channel_params:
n_params_normal = (
in_channels * channels + 9 * channels * channels + channels * 4 * channels
)
n_params_split = C * (in_channels * d + 9 * d * d + d * 4 * channels)
sol = N(solve(n_params_split - n_params_normal, d)[0])
print(
f"in_channels={in_channels}, channels={channels}, n_params={n_params_normal}, C={C}, d={sol:.0f}",
)in_channels=64, channels=64, n_params=57344, C=32, d=5 in_channels=256, channels=64, n_params=69632, C=32, d=4 in_channels=256, channels=128, n_params=245760, C=32, d=9 in_channels=512, channels=128, n_params=278528, C=32, d=8 in_channels=512, channels=256, n_params=983040, C=32, d=18 in_channels=1024, channels=256, n_params=1114112, C=32, d=16 in_channels=1024, channels=512, n_params=3932160, C=32, d=36 in_channels=2048, channels=512, n_params=4456448, C=32, d=32
d は channels を割り切れる必要があるので、通常の Bottleneck より多少パラメータが少くなりますが、
- channels=64 のとき、d=4
- channels=128 のとき、d=8
- in_channels=256 のとき、d=16
- in_channels=512 のとき、d=32
つまり、d = channels * 4 / 64 とします。このモデルは cardinary=32、width=4 なので、ResNext 32x4d と表記します。
cardinary を増やした場合
cardinary=64、width=4 とした場合、Bottleneck Block のパラメータ数は元の ResNet の倍になりますが、cardinary を倍にした場合の精度の検証も論文では行っています。
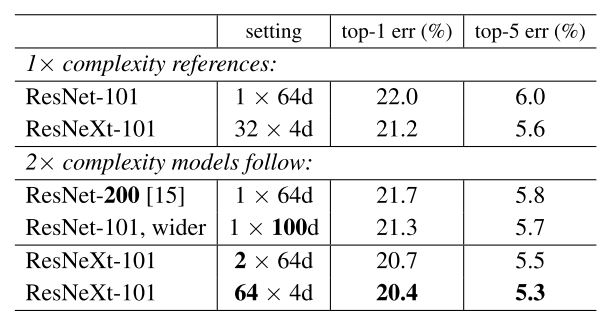
その結果、パラメータ数がほぼ同等である ResNet-200 と ResNeXt-101 64x4d において、ResNeXt のほうが精度がいいことがわかりました。
Grouped Convolution への置き換え
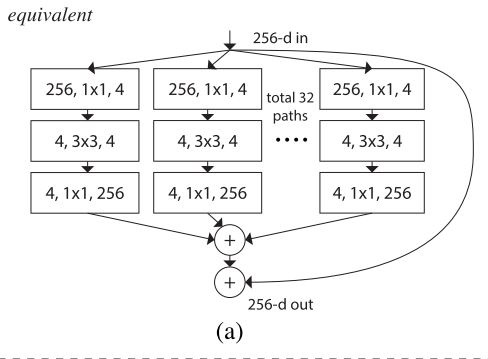
これまで考えてきた分割した Bottleneck (上図 a) は下図 b, c と等価です。そのため、実装上は Grouped Convolution を使用することにします。
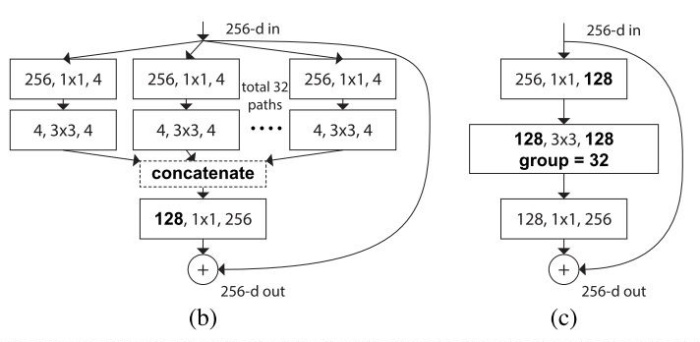
torchvision の ResNeXt の実装
torchvision.models の ResNeXt の実装について解説します。ResNet の実装を一部変更したものなので、ResNet の実装については下記記事で解説し、その変更点のみこの記事で解説します。
[blogcard url=”https://pystyle.info/pytorch-resnet”]
Bottleneck Block の実装
Bottleneck クラスで Bottleneck Block を定義しています。順伝搬時の処理は以下のようになっています。分割後のチャンネル数は int(channels * (width / 64)) なので、Grouped Convolution のチャンネル数は int(channels * (width / 64)) * cardinary で計算します。width=64, cardinary=1 のとき、通常の Bottleneck Block と同じになります。
import torch
import torch.nn as nn
def conv3x3(in_channels, out_channels, stride=1, groups=1):
return nn.Conv2d(
in_channels,
out_channels,
kernel_size=3,
stride=stride,
padding=1,
groups=groups,
bias=False,
)
def conv1x1(in_channels, out_channels, stride=1):
return nn.Conv2d(
in_channels, out_channels, kernel_size=1, stride=stride, bias=False
)
class Bottleneck(nn.Module):
expansion = 4 # 出力のチャンネル数を入力のチャンネル数の何倍に拡大するか
def __init__(
self,
in_channels,
channels,
stride=1,
cardinality=1,
base_width=64,
):
super().__init__()
width = int(channels * (base_width / 64)) * cardinality
self.conv1 = conv1x1(in_channels, width)
self.bn1 = nn.BatchNorm2d(width)
self.conv2 = conv3x3(width, width, stride, groups=cardinality)
self.bn2 = nn.BatchNorm2d(width)
self.conv3 = conv1x1(width, channels * self.expansion)
self.bn3 = nn.BatchNorm2d(channels * self.expansion)
self.relu = nn.ReLU(inplace=True)
# 入力と出力のチャンネル数が異なる場合、x をダウンサンプリングする。
if in_channels != channels * self.expansion:
self.shortcut = nn.Sequential(
conv1x1(in_channels, channels * self.expansion, stride),
nn.BatchNorm2d(channels * self.expansion),
)
else:
self.shortcut = nn.Sequential()
def forward(self, x):
out = self.conv1(x)
out = self.bn1(out)
out = self.relu(out)
out = self.conv2(out)
out = self.bn2(out)
out = self.relu(out)
out = self.conv3(out)
out = self.bn3(out)
out += self.shortcut(x)
out = self.relu(out)
return outResNet を定義する
ResNext クラスで ResNeXt 全体のモデルを作成します。こちらの実装は cardinality, width のパラメータをとるようになった点以外は ResNet と同じです。
class ResNeXt(nn.Module):
def __init__(self, layers, num_classes=1000, cardinality=1, base_width=64):
super().__init__()
self.in_channels = 64 # Residual Block の入力チャンネル数
self.cardinality = cardinality
self.base_width = base_width
self.conv1 = nn.Conv2d(
3, self.in_channels, kernel_size=7, stride=2, padding=3, bias=False
)
self.bn1 = nn.BatchNorm2d(self.in_channels)
self.relu = nn.ReLU(inplace=True)
self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
self.layer1 = self._make_layer(64, layers[0])
self.layer2 = self._make_layer(128, layers[1], stride=2)
self.layer3 = self._make_layer(256, layers[2], stride=2)
self.layer4 = self._make_layer(512, layers[3], stride=2)
self.avgpool = nn.AdaptiveAvgPool2d((1, 1))
self.fc = nn.Linear(512 * Bottleneck.expansion, num_classes)
# 重みを初期化する。
for m in self.modules():
if isinstance(m, nn.Conv2d):
nn.init.kaiming_normal_(m.weight, mode="fan_out", nonlinearity="relu")
elif isinstance(m, nn.BatchNorm2d):
nn.init.constant_(m.weight, 1)
nn.init.constant_(m.bias, 0)
def _make_layer(self, channels, blocks, stride=1):
layers = []
# 最初の Residual Block
layers.append(
Bottleneck(
self.in_channels,
channels,
stride,
cardinality=self.cardinality,
base_width=self.base_width,
)
)
# 残りの Residual Block
self.in_channels = channels * Bottleneck.expansion
for _ in range(1, blocks):
layers.append(
Bottleneck(
self.in_channels,
channels,
cardinality=self.cardinality,
base_width=self.base_width,
)
)
return nn.Sequential(*layers)
def forward(self, x):
x = self.conv1(x)
x = self.bn1(x)
x = self.relu(x)
x = self.maxpool(x)
x = self.layer1(x)
x = self.layer2(x)
x = self.layer3(x)
x = self.layer4(x)
x = self.avgpool(x)
x = torch.flatten(x, 1)
x = self.fc(x)
return xtorchvision では、ResNet-50 の 32x4d のバージョンと、ResNet-101 の 32x8d のバージョンが提供されています。
def resnext50_32x4d():
return ResNeXt([3, 4, 6, 3], cardinality=32, base_width=4)
def resnext101_32x8d():
return ResNeXt([3, 4, 23, 3], cardinality=32, base_width=8)ResNet、ResNext のモデル一覧
| モデル名 | 関数 | パラメータ数 | Top-1 エラー率 | Top-5 エラー率 |
|---|---|---|---|---|
| ResNet-18 | resnet18() | 11689512 | 30.24 | 10.92 |
| ResNet-34 | resnet34() | 21797672 | 26.7 | 8.58 |
| ResNet-50 | resnet50() | 25557032 | 23.85 | 7.13 |
| ResNet-101 | resnet101() | 44549160 | 22.63 | 6.44 |
| ResNet-152 | resnet152() | 60192808 | 21.69 | 5.94 |
| ResNeXt-50-32x4d | resnext50_32x4d() | 25028904 | 22.38 | 6.3 |
| ResNeXt-101-32x8d | resnext101_32x8d() | 88791336 | 20.69 | 5.47 |
| Wide ResNet-50-2 | wide_resnet50_2() | 68883240 | 21.49 | 5.91 |
| Wide ResNet-101-2 | wide_resnet101_2() | 126886696 | 21.16 | 5.72 |


コメント