YOLOv3 – 損失計算や推論結果の生成を行う YOLO レイヤーについて解説

概要

YOLOv3 において、損失の計算や推論結果の生成を行う YOLO レイヤーの実装について解説します。

YOLO レイヤー

YOLO レイヤーは YOLOv3 の出力層にあたる層で、特徴マップを入力とし、学習時には正解ラベルと比較して損失の計算を行い、推論時には矩形やクラスなどの推論結果を生成します。本記事の解説は、論文著者の実装 darknet/yolo_layer.c に従い、解説しています。これを Pytorch で実装したものが pytorch_yolov3/yolo_layer.py になります。

推論結果の生成

YOLO レイヤーが受け取る特徴マップ

YOLOv3 にはスケールが異なる物体を検出できるように、3つの YOLO レイヤーがあります。

YOLO レイヤーは最後の畳み込み層から形状が $(C, H, W)$ の特徴マップを受け取ります。$C$ はチャンネル数、$H, W$ はそれぞれ特徴マップの縦横のグリッド数です。

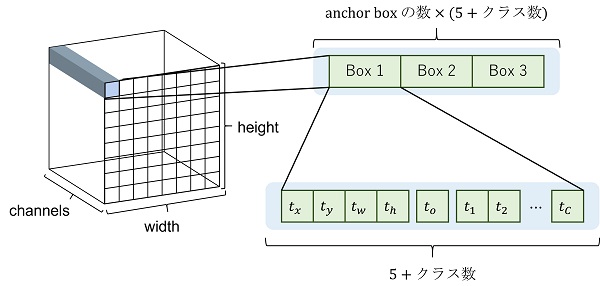
チャンネル数は $(t_x, t_y, t_w, t_h, t_o, t_1, t_2, \cdots, t_C)$ の計 $5 + \text{クラス数}$ の値が anchor box の数だけあるため、$C = \text{anchor box の数} \times (5 + \text{クラス数})$ となっています。

anchor box

anchor box は矩形を出力する際にベースとなる矩形の大きさです。特徴マップの値 $t_w, t_h$ に対して、anchor box の大きさ $a_w, a_h$ 以下の計算式で矩形の大きさ $b_w, b_h$ を計算します。

$$ \begin{aligned} b_w &= e^{t_w} a_w \\ b_h &= e^{t_h} a_h \end{aligned} $$

YOLOv3 では3つの YOLO レイヤーにそれぞれ3つの anchor box が設定されています。この9つの anchor box の大きさは MS COCO データセットから kmeans クラスタリングにより求めたものです。

特徴マップの大きさ

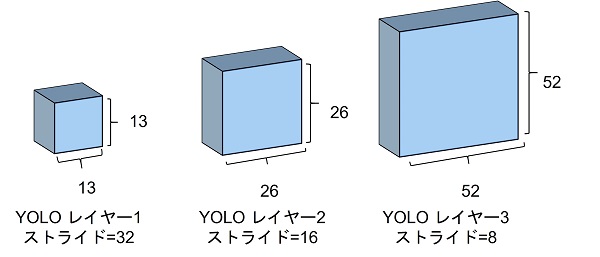
特徴マップの1グリッドが入力画像の何ピクセルに対応するかをストライドといいます。YOLOv3 では3つある YOLO レイヤーのストライドは1つ目は32、2つ目は16、3つ目は32となるようにネットワークが設計されています。例えば、入力サイズが 416×416 の場合、YOLO レイヤーの入力となる特徴マップの形状は1つ目は 13×13、2つ目は 26×26、3つ目は 52×52 となります。

座標系

• 画像座標系
  $I_w, I_h$ を画像の幅及び高さとしたとき、画像の左上を $(0, 0)$、右下を $(I_w, I_h)$ とした座標系です。
• グリッド座標系
  $G_w, G_h$ をグリッドの幅及び高さとしたとき、特徴マップの左上を $(0, 0)$、右下を $(G_w, G_h)$ とした座標系です。
• 正規化された座標系
  画像の左上を $(0, 0)$、右下を $(1, 1)$ とした座標系です。

特徴マップから推論結果を生成する手順

出力 $t_x, t_y, t_w, t_h$ から次のようにしてグリッド座標系における矩形の中心及び大きさを計算します。

矩形の中心 $(b_x, b_y)$ は $t_x, t_y$ にシグモイド関数を適用して値の範囲を $[0, 1]$ にし、グリッドの左上の座標 $(g_i, g_j)$ を加算して計算します。

$$ \begin{aligned} b_x &= g_i + \sigma(t_x) \\ b_y &= g_j + \sigma(t_y) \end{aligned} $$

矩形の大きさ $(b_w, b_h)$ は

$$ \begin{aligned} b_w &= e^{t_w} a_w \\ b_h &= e^{t_h} a_h \end{aligned} $$

で計算します。ただし、$a_w, a_h$ は anchor box の幅及び高さ (グリッド座標系) です。

objectness score はその矩形に検出対象の物体がある確率で、$t_o$ にシグモイド関数を適用して計算します。

$$ p_o = \sigma(t_o) $$

class score は $C$ クラスのそれぞれの確率で、$t_1, t_2, \cdots, t_C$ にシグモイド関数を適用して計算します。

$$ p_i = \sigma(t_i), (i = 1, 2, \cdots, C) $$

ソフトマックス関数でなく、シグモイド関数を使用する理由は1つの矩形にクラスが異なる検出対象が含まれる可能性を考慮するためです。

損失の計算

ラベルに対応する anchor box

YOLO のラベルは $g_c, g_x, g_y, g_w, g_h$ の5つの値で構成されます。$g_c$ はクラス、$g_x, g_y$ は矩形の中心、$g_w, g_h$ は矩形の幅及び高さです。矩形の中心及び幅、高さの座標系は、画像の左上を $(0, 0)$、右下を $(1, 1)$ とした正規化した座標系です。

ラベルは、矩形の大きさと9個の anchor box の大きさとの IOU を計算し、最も IOU が高い anchor box の正解データとなります。それ以外の anchor box の損失計算には関わりません。

矩形 $A$ の大きさを $A_w, A_h$、矩形 $B$ の大きさを $B_w, B_h$ としたとき、2つの矩形の大きさの IOU は次のように計算されます。

$$ \frac{min(A_w, B_w) \times min(A_h, B_h)}{A_w \times A_h + B_w \times B_h – min(A_w, B_w) \times min(A_h, B_h)} $$

ラベルに対応するグリッド

矩形の中心及び大きさ $g_x, g_y, g_w, g_h$ は正規化された座標系の値なので、グリッドの大きさ $(G_w, G_h)$ を乗算することでグリッド座標系に変換できます。

$$ \begin{aligned} g’_x &= G_w g_x \\ g’_y &= G_h g_y \\ g’_w &= G_w g_w \\ g’_h &= G_h g_h \\ \end{aligned} $$

グリッドの位置 $(g’_i, g’_j)$ は $(g’_x, g’_y)$ に床関数をとることで求められます。

$$ \begin{aligned} g’_i &= \lfloor g’_x \rfloor \\ g’_j &= \lfloor g’_y \rfloor \\ \end{aligned} $$

次にラベルが対応する anchor box のうち、最も IOU が高くなるグリッドを求めます。 矩形 $A$ と矩形 $B$ の和の面積を $A \cup B$、共通部分の面積を $A \cap B$ としたとき、IOU は次のように計算します。

$$ \text{IOU} = \frac{A \cap B}{A \cup B} $$

検出対象の物体がある矩形の正解データ

ラベルに対応する anchor box で最も IOU が高くなるグリッドの推論した値が $t_x, t_y, t_w, t_h, t_o, t_1, t_2, \cdots, t_C$ であったとします。シグモイド関数適用済みの $\sigma(t_x), \sigma(t_y), t_w, t_h, \sigma(t_o), \sigma(t_1), \sigma(t_2), \cdots, \sigma(t_C)$ の正解は以下のようになります。

予測値 $\sigma(t_x), \sigma(t_y)$ の正解は、正解の矩形のグリッドの左上の座標から中心を引くことで正解の値を作れます。

$$ \begin{aligned} \sigma(t_x) &\Leftrightarrow g’_x – g’_i \\ \sigma(t_y) &\Leftrightarrow g’_y – g’_j \\ \end{aligned} $$

予測値 $t_y, t_w$ の正解は

$$ \begin{aligned} e^{t_w} a_w &\Leftrightarrow g’_w \\ e^{t_h} a_h &\Leftrightarrow g’_h \\ \end{aligned} $$

より、

$$ \begin{aligned} t_w &\Leftrightarrow \log{\frac{g’_w}{a_w}} \\ t_h &\Leftrightarrow \log{\frac{g’_h}{a_h}} \\ \end{aligned} $$

予測値 $\sigma(t_o)$ の正解は、

$$ \begin{aligned} \sigma(t_o) &\Leftrightarrow 1 \\ \end{aligned} $$

予測値 $\sigma(t_1), \sigma(t_2), \cdots, \sigma(t_C)$ の正解は、正解クラス $g_c$ は1、それ以外は0なので、

$$ \begin{aligned} t_i &\Leftrightarrow \begin{cases} 1 & i = g_c \\ 0 & i \ne g_c \end{cases} \\ \end{aligned} $$

検出対象の物体がない矩形の正解データ

検出対象の物体がない矩形は objectness score が0になるように学習する必要があります。 YOLOv3 では ignore_threshold というパラメータがあり、予測した矩形といずれのラベルの矩形との IOU も ignore_threshold 以下である場合、予測値 $\sigma(t_o)$ の正解は、

$$ \begin{aligned} \sigma(t_o) &\Leftrightarrow 0 \\ \end{aligned} $$

いずれかのラベルと最も IOU が高くなる矩形以外で IOU が ignore_threshold 以上の矩形は損失計算の対象外になります。

重み付け

ラベルの矩形の大きさを $g’_w, g’_h$ としたとき、$t_x, t_y, t_w, t_h$ の損失を計算する際に、その勾配を $2 – \frac{g_w g_h}{G_w G_h}$ でスケールします。$0 \le g’_w g’_h \le G_w G_h$ なので、$1 \le 2 – \frac{g’_w g’_h}{G_w G_h} \le 2$ です。 このような重み付けをする理由は、大きな物体は大雑把に矩形があっていればよいですが、小さい物体は細かい差異でも検出結果の品質に影響が大きいため、小さい物体の矩形のズレに対する損失を高くする目的です。

損失関数

損失関数は項目ごとに計算し、重み付きで和をとって最終的な損失が計算されます。

• $t_x, t_y$: シグモイド関数適用後の値の比較なので、バイナリクロスエントロピー
• $t_w, t_h$: 二乗誤差
• $t_o, t_1, t_2, \cdots, t_C$: シグモイド関数適用後の値の比較なので、バイナリクロスエントロピー

※ 論文では、$t_x, t_y$ の損失は二乗誤差で計算すると書いてありますが、実際の実装 では、シグモイド関数適用後の $\sigma(t_x), \sigma(t_y)$ の値との差分をとっているので、オリジナル実装に従うなら $t_x, t_y$ はバイナリクロスエントロピーで損失を計算します。この差異については以下の issue で議論されています。

• a question about delta_yolo_box · Issue #2733 · AlexeyAB/darknet
• Question about yolo_layer.c · Issue #2287 · AlexeyAB/darknet

参考文献

• YOLO9000: Better, Faster, Stronger
• YOLOv3: An Incremental Improvement