概要
greedy 方策、ε-greedy方策 やボルツマン方策について解説します。
greedy 方策
最適行動価値関数 $Q^*(s, a)$ がわかっていると仮定したとき、現在の状態 $s$ に対して、最適行動価値関数が最大となる行動を選択する方策を greedy 方策といいます。
$$ \pi(a|s) = \begin{cases} 1 &(a = \argmax_a Q^*(s, a)) \\ 0 &(otherwise) \end{cases} $$ε-greedy 方策
実際問題は最適行動価値関数は与えられるものではなく、学習の過程で推定するものです。greedy 方策では、現在推定されている行動価値関数を最大化する行動を選択するため、その時点で推定されている行動価値関数 $Q(s, a)$ では最適でない行動を探索することがなくなってしまいます。そのため、確率 $1 – \varepsilon$ で最適な行動、確率 $\varepsilon$ で行動空間からランダムに行動を選択する方策を $\varepsilon$-greedy方策といいます。最適でない行動はそれぞれ同じ確率 $\frac{\varepsilon}{|A(s)|}$ で選択するものとします。ただし、$|A(s)|$ は行動空間 $A(s)$ の要素数です。
$$ \pi(a|s) = \begin{cases} 1 – \varepsilon + \frac{1}{|A(s)|} &(a = \argmax_a Q(s, a)) \\ \frac{\varepsilon}{|A(s)|} &(otherwise) \end{cases} $$ボルツマン方策
選択確率がギブス分布に従う方策をボルツマン方策または softmax 方策といいます。
$$ \pi(a|s) = \frac{\exp(Q(s, a) / T)}{\sum_{a’ \in A} \exp(Q(s, a’) / T)} $$バンディット問題で検証する
多本腕バンディット問題で各方策の性能を確かめます。多本腕バンディット (multi armed bandit) とは、複数のレバー (腕) がついたスロットで、各レバーを引くと、一定の確率で当たりがでる機械のことです。この問題では、状態は1つで、どのレバーを引くかが行動にあたります。
多本腕バンディット問題の環境
多本腕バンディット問題の環境を定義します。指定した番号のレバーを引くと (アクション)、はずれの場合は0、当たりの場合は報酬1を返します。
import matplotlib.pyplot as plt
import numpy as np
class MultiArmedBanditEnv:
"""多本腕バンディット"""
def __init__(self, num_arms):
self.num_arms = num_arms
self.prob = np.random.rand(num_arms)
def pull(self, no):
"""指定した番号のレバーを引いた場合の結果を返す。"""
return 1.0 if np.random.random() < self.prob[no] else 0.0greedy 方策に従うエージェント
greedy 方策に従うエージェントを作成します。レバーを引いた回数が $k$ 回未満のレバーがある場合、その中からランダムにレバーを選択します。すべてのレバーを $k$ ずつ引いた場合、各レバーの行動価値関数を $k$ 回の報酬の平均で推定し、行動価値関数が最大のレバーを選択します。
class GreedyAgent:
def __init__(self, num_arms, num_plays):
self.num_arms = num_arms
self.num_plays = num_plays
def reset(self):
self.total_rewards = np.zeros(self.num_arms) # 各レバーの得られた報酬
self.play_counts = np.zeros(self.num_arms) # 各レバーの引いた回数
def choice_action(self):
actions = np.where(self.play_counts <= self.num_plays)[0]
if actions.size > 0:
# 引いた回数が num_plays 回以下のレバーがある場合、そのレバーから1つ選ぶ。
return np.random.choice(actions)
# 行動価値関数が最大となるレバーを選択する。
action = self.action_values().argmax()
return action
def percieve(self, action, reward):
self.play_counts[action] += 1
self.total_rewards[action] += reward
def action_values(self):
# これまで得られた報酬の平均で行動価値関数を推定する。
return self.total_rewards / self.play_counts$\varepsilon$-greedy 方策に従うエージェント
$\varepsilon$-greedy 方策に従うエージェントを作成します。レバーを引いた回数が $k$ 回未満のレバーがある場合、その中からランダムにレバーを選択します。すべてのレバーを $k$ ずつ引いた場合、各レバーの行動価値関数を $k$ 回の報酬の平均で推定します。行動の選択は、$1 – \varepsilon$ の確率で行動価値関数が最大のレバー、$\varepsilon$ の確率でそれ以外のレバーを同様の確率で選択します。
class EpsilonGreedyAgent:
def __init__(self, num_arms, num_plays, eps):
self.num_arms = num_arms
self.num_plays = num_plays
self.eps = eps
def reset(self):
self.total_rewards = np.zeros(self.num_arms) # 各レバーの得られた報酬
self.play_counts = np.zeros(self.num_arms) # 各レバーの引いた回数
def choice_action(self):
actions = np.where(self.play_counts <= self.num_plays)[0]
if actions.size > 0:
# 引いた回数が num_plays 回以下のレバーがある場合、そのレバーから1つ選ぶ。
return np.random.choice(actions)
if np.random.rand() <= self.eps:
# eps の確率ですべてのレバーからランダムに選ぶ。
action = np.random.choice(self.num_arms)
else:
# 行動価値関数が最大となるレバーを選択する。
action = self.action_values().argmax()
return action
def percieve(self, arm_no, reward):
self.play_counts[arm_no] += 1
self.total_rewards[arm_no] += reward
def action_values(self):
# これまで得られた報酬の平均で行動価値関数を推定する。
return self.total_rewards / self.play_countsボルツマン方策に従うエージェント
ボルツマン方策に従うエージェントを作成します。レバーを引いた回数が $k$ 回未満のレバーがある場合、その中からランダムにレバーを選択します。すべてのレバーを $k$ ずつ引いた場合、各レバーの行動価値関数を $k$ 回の報酬の平均で推定します。行動の選択は、ギブス分布に従う確率で決定します。
class BoltzmannAgent:
def __init__(self, num_arms, num_plays, T):
self.num_arms = num_arms
self.num_plays = num_plays
self.T = T
def reset(self):
self.total_rewards = np.zeros(self.num_arms) # 各レバーの得られた報酬
self.play_counts = np.zeros(self.num_arms) # 各レバーの引いた回数
def choice_action(self):
actions = np.where(self.play_counts <= self.num_plays)[0]
if actions.size > 0:
# 引いた回数が num_plays 回以下のレバーがある場合、そのレバーから1つ選ぶ。
return np.random.choice(actions)
# ギブス分布に従い、レバーを選択する。
action = np.random.choice(self.num_arms, p=self.action_prob())
return action
def percieve(self, arm_no, reward):
self.play_counts[arm_no] += 1
self.total_rewards[arm_no] += reward
def action_values(self):
# これまで得られた報酬の平均で行動価値関数を推定する。
return self.total_rewards / self.play_counts
def action_prob(self):
return np.exp(self.action_values() / self.T) / np.exp(self.action_values() / self.T).sum()強化学習を行うソルバーを定義する
エージェントと環境を与えると、強化学習を行うソルバーを定義します。
class Solver:
def __init__(self, num_episodes, num_timesteps, env, agent):
self.num_episodes = num_episodes # エピソード数
self.num_timesteps = num_timesteps # 時間ステップ数
self.env = env
self.agent = agent
def solve(self):
avg_rewards = np.zeros(self.num_timesteps)
for i in range(self.num_episodes):
self.agent.reset()
rewards = np.zeros(self.num_timesteps)
for t in range(self.num_timesteps):
# レバーを選択する。(行動の選択)
arm_no = self.agent.choice_action()
# レバーを引く。(行動の実行)
reward = self.env.pull(arm_no)
# 結果をエージェントに伝える。
self.agent.percieve(arm_no, reward)
rewards[t] = reward
# 時刻あたりの平均報酬
avg_rewards += np.cumsum(rewards) / np.arange(1, self.num_timesteps + 1)
return avg_rewards / self.num_episodes学習を実行する
学習を実行し、2つの方策の時間ステップごとの報酬の期待値を確認します。
np.random.seed(0)
num_episodes = 100 # エピソード数
num_timesteps = 5000 # 時間ステップ数
num_arms = 5 # レバーの数
# 環境
env = MultiArmedBanditEnv(num_arms)
# エージェント
greedy_agent = GreedyAgent(num_arms, num_plays=10)
eps_greedy_agent1 = EpsilonGreedyAgent(num_arms, num_plays=10, eps=0.01)
eps_greedy_agent2 = EpsilonGreedyAgent(num_arms, num_plays=10, eps=0.05)
boltzmann_agent = BoltzmannAgent(num_arms, num_plays=10, T=0.05)
greedy_rewards = Solver(num_episodes, num_timesteps, env, greedy_agent).solve()
eps_greedy_rewards1 = Solver(num_episodes, num_timesteps, env, eps_greedy_agent1).solve()
eps_greedy_rewards2 = Solver(num_episodes, num_timesteps, env, eps_greedy_agent2).solve()
boltzmann_rewards = Solver(num_episodes, num_timesteps, env, boltzmann_agent).solve()
# 推定した行動価値関数
print("env", env.prob)
print("greedy", greedy_agent.action_values())
print("ε-greedy (ε=0.01)", eps_greedy_agent1.action_values())
print("ε-greedy (ε=0.05)", eps_greedy_agent2.action_values())
print("Boltzmann", boltzmann_agent.action_values())env [0.5488135 0.71518937 0.60276338 0.54488318 0.4236548 ] greedy [0.61111111 0.70983506 0.6122449 0.45454545 0.45454545] ε-greedy (ε=0.01) [0.59090909 0.7173073 0.41666667 0.5 0.47368421] ε-greedy (ε=0.05) [0.59701493 0.6971211 0.60744501 0.54320988 0.43103448] Boltzmann [0.55084746 0.70702006 0.59921415 0.54025045 0.3902439 ]
グラフで描画する
各時間ステップごとの報酬の平均を可視化します。
# グラフで描写
steps = np.arange(1, num_timesteps + 1)
fig, ax = plt.subplots()
ax.plot(steps, greedy_rewards, label="Greedy")
ax.plot(steps, eps_greedy_rewards1, label="ε-Greedy 0.01")
ax.plot(steps, eps_greedy_rewards2, label="ε-Greedy 0.05")
ax.plot(steps, boltzmann_rewards, label="Boltzmann")
ax.legend()
ax.set_ylim(0.6, 0.7)
ax.set_xlabel("Steps")
ax.set_ylabel("Rewards")
ax.grid()
plt.show()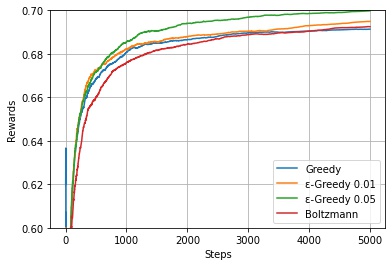
$\varepsilon$-greedy 方策のほうが、greedy 方策より各時間ステップでの得られる報酬の期待値が高いことがわかります。


コメント