強化学習 – 状態価値関数、行動価値関数について

概要

強化学習の概要について解説します。

強化学習

学習と意思決定を行う者をエージェント (agent)、エージェントが相互作用を行う対象を環境 (environment)といいます。エージェントと環境の相互作用から学習して目標を達成する仕組みのことを強化学習といいます。 エージェントは現在の状態 (status)から行動 (action)を取ります。すると、環境から行動により変化した状態及び報酬 (reward)が得られます。強化学習の目標は、エージェントが報酬が多くなるような行動が選択できるように学習することです。

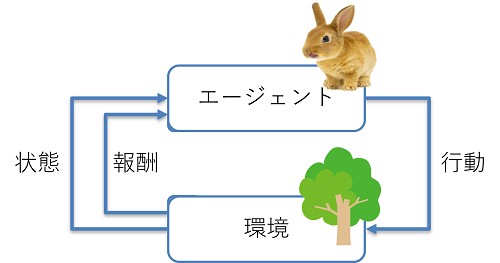
強化学習は、ゲームやロボットの行動の学習など、人間が正解を定義する教師あり学習が難しい例に向いています。

時間ステップとエピソード

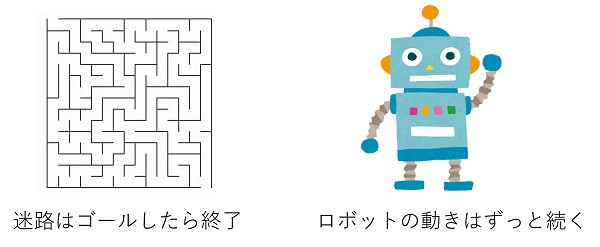
エージェントが行動を選択し、その結果である状態と報酬を環境から受け取るという1サイクルを時間ステップといいます。 強化学習で解きたい問題には次の2種類あります。

• 迷路のように終了が定義できる問題
• ロボットの動きのように終了が定義できない問題

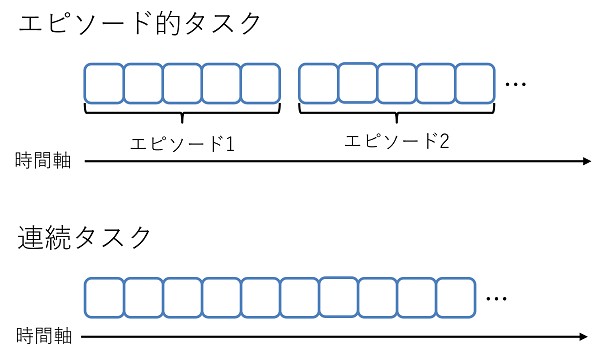
終了が定義できる問題において、開始してから終了するまでの一連の流れを1エピソードといいます。

エージェントの方策

エージェントがある状態のときに、どのような行動をとるかを決める指針を方策 (policy)といいます。できるだけ多くの報酬がもらえるようこの方策を調整することがエージェントの学習になります。ある状態において、行動を一意に決定する方法を決定方法、確率的に決定する方法を確率方策といいます。確率方策の場合、現在の状態が $s$ のとき、行動 $a$ を決定する確率を $\pi(a|s)$ で表します。

マルコフ決定過程

いくつか用語を定義します。

• 環境のとり得る状態の集合のことを状態空間といい、$S$ で表します。
• 現在の状態が $s$ であるとき、選択可能な行動の集合を行動空間といい、$A(s)$ で表します。
• マルコフ決定過程において、現在の状態からある行動を選択したとき、次の状態に遷移する確率は、現在の状態、選択した行動によってのみ決まり、それより過去の状態や行動には左右されないと仮定します。このことをマルコフ性といいます。現在の状態が $s$ であるとき、行動 $a$ を選択したとき、状態 $s’$ に遷移する確率を状態遷移確率といい、$p(s’|a, s)$ で表します。
• 初期の状態が $s$ である確率を初期状態確率といい、$p_0(s)$ で表します。

時間ステップ $t$ における状態、選択する行動、得られる報酬は、初期状態確率及び状態遷移確率によって確率的に決まるため、確率変数となります。これらを表す記法を定義します。

• 時間ステップ $t$ の状態を表す確率変数を $S_t$ で表します。
• 時間ステップ $t$ の状態 $S_t$ において、選択された行動を表す確率変数を $A_t$ で表します。
• 時間ステップ $t$ の状態 $S_t$ において、行動 $A_t$ が選択されたとき、得られる報酬を表す確率変数を $R_{t + 1}$ で表します。

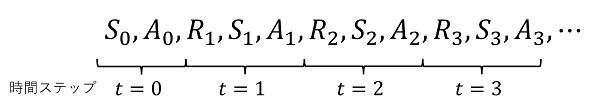
$S_0$ は一番最初の状態を表し、これは確率分布 $p_0$ に従って、決まります。これを初期状態分布といいます。

$$S_0 \sim p_0$$

マルコフ性より、次の状態 $S_{t + 1}$ は、現在の状態 $S_t$ 及び選択した行動 $A_t$ によって決まるので、

$$S_{t + 1} \sim p(s’|S, A)$$

環境は、現在の状態 $S_t$、選択した行動 $A_t$、遷移後の状態 $S_{t + 1}$ によって、報酬を決定します。

$$R_{t + 1} = r(S_t, A_t, S_{t + 1})$$

収益

例えば、ゲームが終了した時点で報酬が確定する場合、直近の報酬ではなく、将来得られる報酬も考慮する必要があります。そのため、ある期間で得られる報酬を収益として次のように定義します。

$$G_t = \sum_{\tau = 0}^T R_{t + 1 + \tau}$$

$T$ はどのくらい先の時間ステップの報酬までを考慮するかを決定する区間です。より長期的な区間の報酬を考慮する場合、$T \to \infty$ とすると、$G_t$ が発散してしまうため、次のように平均で収益を定義することもあります。

$$G_t = \lim_{T \to \infty} \frac{1}{T} \sum_{\tau = 0}^T R_{t + 1 + \tau}$$

また、直近の報酬をより重視する場合、割引率 $\gamma, (0 \le \gamma \le 1)$ を導入し、収益を次の割引報酬和で定義することもあります。

$$G_t = \sum_{\tau = 0}^\infty \gamma^\tau R_{t + 1 + \tau} = R_{t + 1} + \gamma R_{t + 2} + \gamma^2 R_{t + 3} + \cdots$$

$\gamma$ が0に近いほど、直近の報酬がより重視されるようになります。

状態価値、状態価値関数

収益は確率変数である報酬の和なので、確率変数です。 現在の状態 $s$ から方策 $\pi$ に従って行動を決定した場合に得られる収益の期待値を状態価値 (state value) といい、これは現在の状態 $s$ と方策 $\pi$ に依存するので、$V^\pi(s)$ で表します。

$$V^\pi(s) = E^\pi [G_t|S_t = s]$$

$\pi$ を固定して、$s$ を変化させた場合、様々な $s$ に対する状態価値を計算できます。これを状態価値関数といいます。 $s$ を固定して、$\pi$ を変化させた場合、様々な方策 $\pi$ に対する状態価値を計算できます。ある状態 $s$ のとき、2つの方策 $\pi, \pi’$ があるとき、

$$V^\pi(s) \le V^{\pi’}(s)$$

であれば、状態 $s$ においては方策 $\pi’$ のほうが優れているといえます。この不等式が成り立つかは状態 $s$ によって変わってくるので、任意の状態 $s \in S$ において、

$$V^\pi(s) \le V^{\pi’}(s)$$

が成り立つならば、方策 $\pi$ より $\pi’$ のほうが優れていると定義します。また、任意の状態 $s \in S$ において、

$$V^\pi(s) = V^{\pi’}(s)$$

が成り立つならば、$\pi, \pi’$ は同じ方策であると定義します。

最適方策、最適状態価値関数

任意の $s$ に対して、状態価値関数を最大化する方策を最適方策といい、$\pi^*$ で表すことにします。つまり、

$$\forall \pi, \forall s \in S, V^\pi(s) \le V^{\pi^*}(s)$$

が成り立ちます。最適方策は次の式を満たします。

$$\forall s \in S, V^*(s) = V^{\pi^*}(s) = \max_\pi V^\pi (s)$$

この $V^*(s)$ を最適状態価値関数といいます。

行動価値、行動価値関数、最適行動価値関数

状態価値に、選択した行動も条件とした

$$Q^\pi(s, a) = E^\pi [G_t| S_t = s, A_t = a]$$

の値を状態 $s$ から行動 $a$ を選択したときの行動価値といいます。$\pi$ を固定して、$s, a$ を変化させた場合、様々な $s, a$ に対する行動価値を計算できます。これを行動価値関数といいます。状態関数と同様に最適行動価値関数を定義します。

$$\forall s \in S, \forall a \in A(s), Q^*(s, a) = Q^{\pi^*}(s, a) = \max_\pi Q^\pi (s, a)$$