概要
全確率の定理、ベイズの定理について解説します。
全確率の定理
定義 – 分割
事象 $A_1, A_2, \cdots$ について、$A_i \cap A_j = \emptyset, (i \ne j; i, j = 1, 2, \cdots)$ かつ $\bigcup_{i = 1}^\infty A_i = \Omega$ を満たすとき、$A_1, A_2, \cdots$ を標本空間 $\Omega$ の分割という。
定理 – 全確率の定理 (law of total probability)
証明:
$$ \begin{aligned} B &= B \cap \Omega \\ &= B \cap \left( \bigcup_{i = 1}^\infty A_i \right) \\ &= \bigcup_{i = 1}^\infty (B \cap A_i) \quad \because 分配則 \end{aligned} $$$(B \cap A_i) \cap (B \cap A_j) = \emptyset, (i \ne j; i, j = 1, 2, \cdots)$ であるから、
$$ \begin{aligned} P(B) &= P \left(\bigcup_{i = 1}^\infty (B \cap A_i) \right) \\ &= \sum_{i = 1}^\infty P(B \cap A_i) \quad \because 可算加法性 \\ &= \sum_{i = 1}^\infty P(A_i)P(B|A_i) \quad \because 乗法定理 \end{aligned} $$系 全確率の定理 (有限個の場合)
例1
ある工場では、3つの機械 A, B, C で製品を作っている。 機械 A で作った製品の中には10%、機械 B の製品の中には20%、機械 C の製品の中には5%の確率で不良品が発生するという。 今、この工場では50%の製品を機械Aで、30%の製品を機械Bで、20%の製品を機械Cで作っているとする。 できあがった製品を1つ取り出したとき、それが不良品である確率はいくらか。
解答: $\Omega$ を「工場で作られた製品をとる」という試行の標本空間とする。 事象を次のように定める。
$$ \begin{aligned} A &= \{ \omega \in \Omega; \omega は機械 A で作られた \} \\ B &= \{ \omega \in \Omega; \omega は機械 B で作られた \} \\ C &= \{ \omega \in \Omega; \omega は機械 C で作られた \} \\ D &= \{ \omega \in \Omega; \omega は不良品である \} \end{aligned} $$問題設定より、
$P(A) = 0.5, P(B) = 0.3, P(C) = 0.2$、$P(D|A) = 0.1, P(D|B) = 0.2, P(D|C) = 0.05$ である。
$A, B, C$ は $\Omega$ の分割であるから、全確率の定理より、
$$ \begin{aligned} P(D) &= P(A)P(D|A) + P(B)P(D|B) + P(C)P(D|C) \\ &= 0.5 \times 0.1 + 0.3 \times 0.2 + 0.2 \times 0.05 = 0.12 \end{aligned} $$例2
箱 $A_1$ には黒玉1個、赤玉2個が入っている。箱 $A_2$ には黒玉1個、赤玉3個が入っている。箱をランダムに選んで、玉を1個取り出して確認する試行を考える。このとき、取り出した玉が赤玉である確認を求めよ。
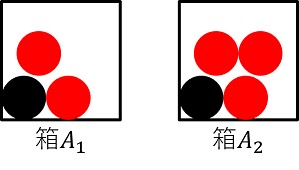
解答)
$\Omega$ を「箱を選んで、その箱から玉を1つ取り出す」という試行の標本空間とする。 $A_1$ を箱 $A_1$ を選ぶ事象、$A_2$ を箱 $A_2$ を選ぶ事象とする. $R$ を取り出した玉が赤である事象とする。
箱はランダムに選ぶので、$P(A_1) = \frac{1}{2}, P(A_2) = \frac{1}{2}$
また、箱に入っている玉の数より $(R|A_1) = \frac{2}{3}, P(R|A_2) = \frac{3}{4}$ である。
$A_1, A_2$ は $\Omega$ の分割であるから、全確率の定理より、
$$ \begin{aligned} P(R) &= P(A_1)P(R|A_1) + P(A_2)P(R|A_2) \\ &= \frac{1}{2} \times \frac{2}{3} + \frac{1}{2} \times \frac{3}{4} = \frac{17}{24} \end{aligned} $$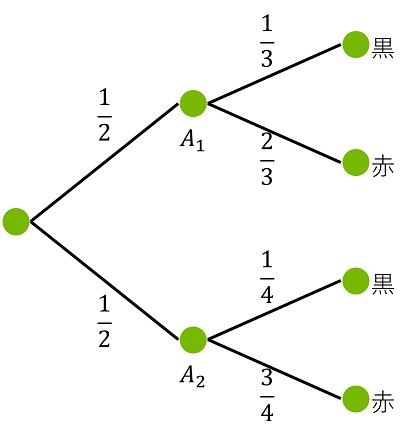
ベイズの定理 (Bayes theorem)
定理 – ベイズの定理
証明:
$P(A_i) > 0, (i = 1, 2, \cdots)$ であるから、乗法定理より、
$$ P(A_i \cap B) = P(A_i)P(B|A_i) $$全確率の定理より、
$$ P(B) = \sum_{i = 1}^\infty P(A_i) P(B|A_i) $$$P(B) > 0$ であるから、条件付き確率の定義より、
$$ P(A_i|B) = \frac{P(A_i \cap B)}{P(B)} = \frac{P(A_i)P(B|A_i)}{\sum_{j = 1}^\infty P(A_j)P(B|A_j)} $$系 – ベイズの定理 (有限個の場合)
このとき、$P(B) > 0$ である事象 $B$ に対して、次が成り立つ。
$$ \begin{aligned} P(A_i|B) &= \frac{P(A_i)P(B|A_i)}{\sum_{j = 1}^\infty P(A_j)P(B|A_j)} \\ &= \frac{P(A_i)P(B|A_i)}{P(B)}, (i = 1, 2, \cdots, n) \end{aligned} $$
例 – 3囚人問題
3人の囚人 A、B、C は保釈になるチャンスは同じであるが、3人のうち1人だけが今回保釈になるという。 看守は誰が保釈になるか知っているが、保釈される本人には言えない。 今、囚人 A が看守に他の2人のうちどちらかが保釈されないかを尋ねたところ、B は保釈されないと答えた。 この看守は正直者だとすると、A の保釈される確率は $\frac{1}{2}$ になるかどうか。
解答: 「3人のうち一人が保釈されるとき、A が看守に他の二人のどちらが保釈されないかを聞く」という試行を考える。 A が保釈される事象を $A$、Bが保釈される事象を $B$、Cが保釈される事象を $C$、看守がBは保釈されないと答える事象を $K$ とする。 「3人の囚人 A、B、C は保釈になるチャンスは同じ」であるから、
$$ P(A) = P(B) = P(C) = \frac{1}{3} $$A が保釈されるとき、B と C は両方保釈されないが、看守が B は保釈されないと答える確率は $\frac{1}{2}$ とすると、
$$ P(K \cap A) = \frac{1}{3} \times \frac{1}{2} = \frac{1}{6} $$B が保釈されるとき、B が保釈されると答えることは起こり得ないので、
$$ P(K \cap B) = 0 $$C が保釈されるとき、B が保釈されないと必ず答えるので、
$$ P(K \cap C) = \frac{1}{3} \times 1 = \frac{1}{3} $$よって、条件付き確率の定義より、
$$ \begin{aligned} P(K|A) &= \frac{P(A \cap K)}{P(A)} = \frac{1}{2} \\ P(K|B) &= \frac{P(B \cap K)}{P(B)} = 0 \\ P(K|C) &= \frac{P(C \cap K)}{P(C)} = 1 \end{aligned} $$ベイズの定理より、
$$ \begin{aligned} P(A|K) &= \frac{P(A)P(K|A)}{P(A)P(K|A) + P(B)P(K|B) + P(C)P(K|C)} \\ &= \frac{\frac{1}{3} \times \frac{1}{2}}{\frac{1}{3} \times \frac{1}{2} + \frac{1}{3} \times 0 + \frac{1}{3} \times 1} \\ &= \frac{1}{3} \end{aligned} $$よって、A の保釈される確率は最初から変化していない。
定義 – 事前確率、事後確率
事象 $B$ が与えられたとき、事象 $A_i$ が起こる条件付き確率 $P(A_i|B)$ を $A_i$ の事後確率 (posterior probability) という。また、$P(B|A_i)$ を事前確率 (prior probability) という。


コメント