概要
連続確率分布の1つであるカイ二乗分布について解説します。
確率関数
確率変数 $X$ が次の確率密度関数をもつとき、$X$ は自由度 (degrees of freedom) $n$ の(中心)カイ二乗分布 (chi squared distribution) または $\chi^2$ 分布に従うという。
確率変数 $X$ が自由度 $n$ のカイ二乗分布に従うとき、$X \sim \chi_n^2$ と表す。
$$ f_X(x) = \begin{cases} f_X(x) = \frac{1}{2^\frac{n}{2} \Gamma(\frac{n}{2})} x^{\frac{n}{2} – 1} e^{- \frac{x}{2}} & x > 0 \\ 0 & その他の場合 \end{cases} $$ただし、$\Gamma(\cdot)$ はガンマ関数、$n \in \N$ は正の整数とする。
確率密度関数の要件を満たしている
(1) $f_X(x) \ge 0$ は明らか
(2) 規格化
$$ \begin{aligned} \int_{-\infty}^{\infty} f_X(x) dx &= \frac{1}{2^\frac{n}{2} \Gamma(\frac{n}{2})} \int_{-\infty}^{\infty} x^{\frac{n}{2} – 1} e^{- \frac{x}{2}} dx \\ &= \frac{1}{2^\frac{n}{2} \Gamma(\frac{n}{2})} \int_{-\infty}^{\infty} (2y)^{\frac{n}{2} – 1} e^{-y} dy \quad \because \frac{x}{2} = y と置換積分 \\ &= \frac{1}{2 \Gamma(\frac{n}{2})} \cdot 2 \Gamma\left(\frac{n}{2}\right) \quad \because ガンマ関数の定義 \\ &= 1 \end{aligned} $$ガンマ分布との関係
自由度 $n$ のカイ二乗分布はパラメータ $\alpha = \frac{n}{2} \beta = \frac{1}{2}$ としたときのガンマ分布である。
指数分布との関係
自由度2のカイ二乗分布は $\alpha = 1 \beta = \frac{1}{2}$ としたときの指数分布であるから、パラメータ $\beta = \frac{1}{2}$ の指数分布である。
k 次積率
ガンマ分布の $k$ 次積率に $\alpha = \frac{n}{2} \beta = \frac{1}{2}$ と代入すると、
$$ \begin{aligned} E(X^k) &= \frac{\alpha (\alpha + 1) \cdots (\alpha + k – 1)}{\beta^k} \end{aligned} $$期待値
パラメータ $\alpha, \beta$ のガンマ分布の期待値に $\alpha = \frac{n}{2} \beta = \frac{1}{2}$ と代入すると、
$$ E[X] = \frac{\alpha}{\beta} = n $$分散
パラメータ $\alpha, \beta$ のガンマ分布の分散に $\alpha = \frac{n}{2} \beta = \frac{1}{2}$ と代入すると、
$$ Var[X] = \frac{\alpha}{\beta^2} = 2n $$標準偏差
$$ Std[X] = \sqrt{Var[X]} = \sqrt{2n} $$積率母関数
パラメータ $\alpha, \beta$ のガンマ分布の積率母関数は $t < \beta$ で定義されるので、$t < \frac{1}{2}$ としたとき、 $\alpha = \frac{n}{2} \beta = \frac{1}{2}$ と代入すると、
$$ \begin{aligned} m_X(t) &= \left(\frac{1}{1 – 2t}\right)^{\frac{n}{2}} \end{aligned} $$再生性
$X_1, X_2, \cdots, X_n$ が独立でそれぞれ自由度 $k_i$ のカイ二乗分布に従うとき、 $S = X_1 + X_2 + \cdots + X_n$ は自由度 $k_1 + k_2 + \cdots + k_n$ のカイ二乗分布に従う。
証明:
$X_i$ の積率母関数を $m_{X_i}(t)$ とすると、
$$ m_S(t) = \prod_{i = 1}^n m_{X_i}(t) = \left(\frac{1}{1 – 2t}\right)^{\frac{k_1 + k_2 + \cdots + k_n}{2}} $$これは自由度 $k_1 + k_2 + \cdots + k_n$ のカイ二乗分布の積率母関数と一致する。 積率母関数の一意性より、題意は示された。
標準正規分布との関係
$Z$ が標準正規分布に従うとき、$Y = Z^2$ は自由度1のカイ二乗分布に従う。
証明:
$$ \begin{aligned} m_Y(t) &= E[e^{tY}] \\ &= E[e^{tZ^2}] \\ &= \int_{-\infty}^{\infty} e^{tz^2} \frac{1}{\sqrt{2 \pi}} \exp \left(-\frac{z^2}{2}\right) dz \\ &= \int_{-\infty}^{\infty} \frac{1}{\sqrt{2 \pi}} \exp \left(\frac{-(1 – 2t)z^2}{2}\right) dz \\ &= \frac{1}{\sqrt{1 – 2t}} \int_{-\infty}^{\infty} \frac{\sqrt{1 – 2t}}{\sqrt{2 \pi}} \exp \left(\frac{-(1 – 2t)z^2}{2}\right) dz \\ \end{aligned} $$ここで、
$$ \int_{-\infty}^{\infty} \frac{\sqrt{1 – 2t}}{\sqrt{2 \pi}} \exp \left(\frac{-(1 – 2t)z^2}{2}\right) dz $$は、平均 $\mu = 0$、分散 $\sigma^2 = \frac{1}{\sqrt{1 – 2t}}$ としたときの正規分布の全実数についての積分なので、1となる。
よって、
$$ m_Y(t) = \left(\frac{1}{1 – 2t}\right)^\frac{1}{2} $$これは自由度 $1$ のカイ二乗分布の積率母関数と一致する。 積率母関数の一意性より、題意は示された。
標準正規分布との関係
$Z_1, Z_2, \cdots, Z_n$ が独立でそれぞれ標準正規分布に従うとき、 $Y = Z_1^2 + Z_2^2 + \cdots + Z_n^2$ は自由度 $n$ のカイ二乗分布に従う。
証明:
$Z^2$ は自由度1のカイ二乗分布に従うので、カイ二乗分布の再生性より、 $Y$ は自由度 $n$ のカイ二乗分布に従う。
正規分布との関係
$X_1, X_2, \cdots, X_n$ が独立でそれぞれ平均 $\mu_i$、分散 $\sigma^2$ の正規分布に従うとき、 $Y = \sum_{i = 1}^n \left(\frac{X_i – \mu_i}{\sigma_i}\right)^2$ は自由度 $n$ のカイ二乗分布に従う。
証明:
$Z_i = \frac{X_i – \mu_i}{\sigma_i}$ とすると、$Z_i$ は標準正規分布に従うので、$Y$ は自由度 $n$ のカイ二乗分布に従う。
scipy.stats のカイ二乗分布
scipy.stats.chi2 でカイ二乗分布に従う確率変数を作成できます。
import numpy as np
import seaborn as sns
from matplotlib import pyplot as plt
from scipy.stats import chi2
sns.set(style="white")
X = chi2(10)サンプリング
x = X.rvs(size=5)
print(x)[14.21866758 17.01161969 9.51196718 13.50533751 14.14309324]
確率密度関数
x = np.linspace(0, 30, 100)
y = X.pdf(x)
fig, ax = plt.subplots()
ax.plot(x, y)
ax.grid()
plt.show()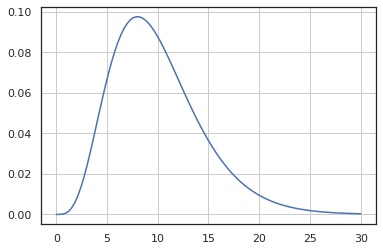
累積分布関数
x = np.linspace(0, 30, 100)
y = X.cdf(x)
fig, ax = plt.subplots()
ax.plot(x, y)
ax.grid()
plt.show()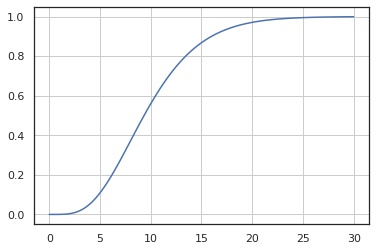
統計量
print("mean", X.mean())
print("var", X.var())
print("std", X.std())mean 10.0 var 20.0 std 4.47213595499958


コメント