目次
概要
連続確率分布の1つである一様分布について解説します。
確率密度関数
確率変数 $X$ が次のような確率密度関数をもつとき、$X$ は区間 $[a, b]$ の(連続)一様分布 (uniform distribution) に従うという。
$$ f_X(x) = \begin{cases} \frac{1}{b – a} & a \le x \le b \\ 0 & その他の場合 \end{cases} $$確率密度関数である
$$ \int_{-\infty}^{\infty} \frac{1}{b – a} dt = \frac{1}{b – a} [t]^b_a dt = 1 $$累積確率関数
$$ P(X \le x) = \int_{-\infty}^x \frac{1}{b – a} dt $$$x < a$ の場合、$f_X(x) = 0$ なので、
$$ \int_{-\infty}^x \frac{1}{b – a} dt = 0 $$$a \le x \le b$ の場合、
$$ \int_{-\infty}^x \frac{1}{b – a} dt = \int_a^x \frac{1}{b – a} dt = \frac{x – a}{b – a} $$$x > b$ の場合、$f_X(x) = 0, (x < a, x > b)$ なので、
$$ \int_{-\infty}^x \frac{1}{b – a} dt = \int_a^b \frac{1}{b – a} dt = 1 $$よって、
$$ P(X \le x) = \begin{cases} 0 & x < a \\ \frac{x – a}{b – a} & a \le x \le b \\ 1 & x > b \end{cases} $$k 次積率
$$ \begin{aligned} E[X^k] &= \int_a^b x^k \frac{1}{b – a} dx \\ &= \frac{1}{b – a} \left[\frac{x^{k + 1}}{k + 1}\right]_a^b \\ &= \frac{1}{b – a} \frac{b^{k + 1} – a^{k + 1}}{k + 1} \end{aligned} $$ここで、$b^k – a^k = (b – a) \sum_{i = 0}^{k – 1} a^i b^{k – 1 – i}$ を利用すると、
$$ \begin{aligned} \frac{1}{b – a} \frac{b^{k + 1} – a^{k + 1}}{k + 1} &= \frac{1}{k + 1} \frac{(b – a) \sum_{i = 0}^k a^i b^{k – i}}{b – a} \\ &= \frac{1}{k + 1} \sum_{i = 0}^k a^i b^{k – i} \end{aligned} $$期待値
$k$ 次積率の結果より、
$$ \begin{aligned} E[X] = \frac{a + b}{2} \end{aligned} $$分散
$k$ 次積率の結果より、
$$ E[X^2] = \frac{1}{3} (a^2 + ab + b^2) $$$$ \begin{aligned} Var[X] &= E[X^2] – [E(X)]^2 \\ &= \frac{1}{3} (a^2 + ab + b^2) – \frac{(a + b)^2}{4} \\ &= \frac{a^2 – 2ab – b^2}{12} \\ &= \frac{(b – a)^2}{12} \end{aligned} $$標準偏差
$$ Std[X] = \sqrt{Var[X]} = \frac{b – a}{2 \sqrt{2}} $$積率母関数
$$ \begin{aligned} m_X(t) &= E[e^{tX}] \\ &= \frac{1}{b – a} \int_a^b e^{tx} dx \\ &= \frac{1}{b – a} \left[\frac{e^{tx}}{t}\right]_a^b \\ &= \frac{e^{tb} – e^{ta}}{t(b – a)} \end{aligned} $$scipy.stats の一様分布
scipy.stats.uniform で一様分布に従う確率変数を作成できます。
In [1]:
import numpy as np
import seaborn as sns
from matplotlib import pyplot as plt
from scipy.stats import uniform
sns.set(style="white")
X = uniform(loc=-2, scale=4)サンプリング
In [2]:
x = X.rvs(size=5)
print(x)[-0.17091662 -0.53469003 1.35470988 -1.71785535 1.02110735]
確率密度関数
In [3]:
x = np.linspace(-5, 5, 100)
y = X.pdf(x)
fig, ax = plt.subplots()
ax.plot(x, y)
ax.grid()
plt.show()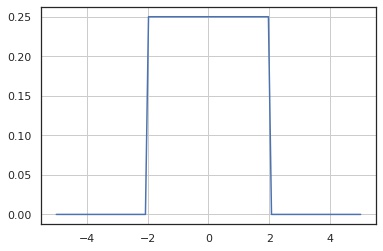
累積分布関数
In [4]:
x = np.linspace(-5, 5, 100)
y = X.cdf(x)
fig, ax = plt.subplots()
ax.plot(x, y)
ax.grid()
plt.show()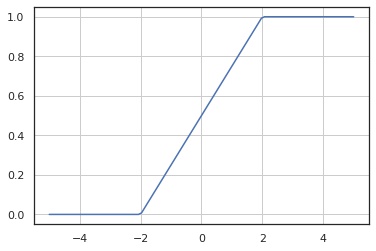
統計量
In [5]:
print("mean", X.mean())
print("var", X.var())
print("std", X.std())mean 0.0 var 1.3333333333333333 std 1.1547005383792515


コメント