概要
最尤法による直線フィッティングについて解説し、Python による実装例を紹介します。
最尤法によるアプローチ
問題設定
直線フィッティングの目標は、$N$ 個の入力値 $\bm{x} = (x_1, x_2, \cdots, x_N)^T$ とそれに対応する目標値 $\bm{t} = (t_1, t_2, \cdots, t_N)^T$ で構成される訓練集合に基づいて、新たな入力値 $x$ が与えられたとき、対応する目標値 $t$ の予測ができるようになることです。
目標変数に対する不確実性は確率分布を使って表します。 与えられた入力値 $x$ に対して、対応する目標値 $t$ は、平均が多項式曲線 $y(x; \bm{w})$、分散が $\sigma^2$ の正規分布に従うものとします。ここで、$\beta^{-1} = \sigma^2$ とおくと、$t$ の分布は
$$ p(t;x, \bm{w}, \beta) = N(t; y(x; \bm{w}), \beta^{-1}) $$最尤法によるパラメータ推定
訓練データの目標値がこの分布から独立にとられたものであると仮定すると、尤度関数は
$$ L(\bm{t}|\bm{x}, \bm{w}, \beta) = \prod_{i = 1}^N N(t_i; y(x_i; \bm{w}), \beta^{-1}) $$対数尤度関数にして、正規分布の確率密度関数を展開すると、
$$ \begin{aligned} \log L(\bm{t}|\bm{x}, \bm{w}, \beta) &= \sum_{i = 1}^N \log N(t_i; y(x_i; \bm{w}), \beta^{-1}) \\ &= – \frac{N}{2} \log (2 \pi) + \frac{N}{2} \log \beta – \frac{\beta}{2} \sum_{i = 1}^N (t_i – y(x_i; \bm{w}))^2 \\ \end{aligned} $$$\bm{w}$ の最尤推定値を考えると、
$$ \begin{aligned} \hat{\bm{w}} &= \argmax_{\bm{w}} \log L(\bm{t}|\bm{x}, \bm{w}, \beta) \\ &= \argmax_{\bm{w}} -\frac{\beta}{2} \sum_{i = 1}^N (t_i – y(x_i; \bm{w}))^2 \\ &= \argmin_{\bm{w}} \frac{\beta}{2} \sum_{i = 1}^N (t_i – y(x_i; \bm{w}))^2 \\ &= \argmin_{\bm{w}} \frac{1}{2} \sum_{i = 1}^N (t_i – y(x_i; \bm{w}))^2 \end{aligned} $$となり、二乗誤差の最小化と等価であることがわかります。したがって、二乗誤差の最小化は、ノイズがガウス分布に従うという仮定での尤度関数の最大化の結果としてみなせます。
$\beta$ の最尤推定値を考えると、尤度方程式は
$$ \begin{aligned} \frac{\hat{\beta}}{d \hat{\beta}} \log L(\bm{t}|\bm{x}, \hat{\bm{w}}, \hat{\beta}) &= \frac{N}{2 \hat{\beta}} – \frac{1}{2} \sum_{i = 1}^N (t_i – y(x_i; \hat{\bm{w}}))^2 = 0 \end{aligned} $$これを解くと、
$$ \frac{1}{\hat{\beta}} = \frac{1}{N} \sum_{i = 1}^N (t_i – y(x_i; \hat{\bm{w}}))^2 $$$\hat{\bm{w}}, \hat{\beta}$ が決まれば、新たな入力値 $x$ に対して、目標値 $t$ を $t$ の確率分布という形で計算できようになります。これを予測分布 (predictive distribution) といいます。
$$ p(t;x, \hat{\bm{w}}, \hat{\beta}) = N(t; y(x; \hat{\bm{w}}), \hat{\beta}^{-1}) $$Python による実装例
訓練集合を作成する
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from numpy.polynomial import polynomial as P
from scipy.stats import norm
np.random.seed(0)
# パラメータ
sigma = 0.2 # ノイズの標準偏差
def make_dataset(n, noise=False):
x = np.linspace(0, 1, n)
y = np.sin(2 * np.pi * x)
if noise:
y += np.random.normal(0, sigma, n)
return x, y
# 訓練集合、テスト集合を作成する。
x_train, y_train = make_dataset(10, noise=True)
x, y = make_dataset(100)
# 描画する。
fig, ax = plt.subplots()
ax.grid()
ax.scatter(x_train, y_train, s=50, fc="none", ec="b", label="train")
ax.plot(x, y, "g", label="$\sin(2 \pi x)$")
ax.legend()
plt.show()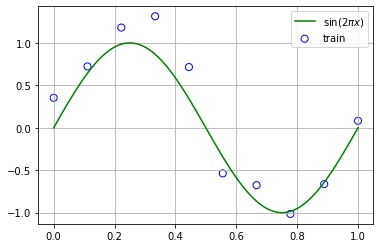
最尤推定値を求める
最尤推定値 $\hat{\bm{w}}, \hat{\beta}$ を求めます。
# w の尤度
w_ml = P.polyfit(x_train, y_train, 3)
# w の尤度
model = P.Polynomial(w_ml)
beta_ml = 1 / np.mean((y_train - model(x_train)) ** 2)
# sigma に直すと
sigma_ml = np.sqrt(1 / beta_ml)
print(f"w_ml: {w_ml}")
print(f"beta_ml: {beta_ml} (sigma_ml: {sigma_ml})")w_ml: [ 0.18106302 11.3901447 -34.34938915 22.88651559] beta_ml: 22.178339939836093 (sigma_ml: 0.2123417939179997)
グラフを描画する
以下のグラフを描画します。
- $sin(2 \pi x)$ (緑の折れ線)
- 学習集合の入力値と目標値 $(x, t)$ (青丸の点)
- 最小二乗法により近似した曲線 $y(x_i; \hat{\bm{w}})$ (赤の折れ線)
- 各 $t$ における $p(t;x, \hat{\bm{w}}, \hat{\beta})$ の分布の5%パーセンタイル点と95パーセンタイル点の値 (青色の帯)
y_pred = model(x)
# 各 y(x;w) の
p5 = [norm.ppf(q=0.05, loc=mu, scale=sigma_ml) for mu in y_pred]
p95 = [norm.ppf(q=0.95, loc=mu, scale=sigma_ml) for mu in y_pred]
# 描画する。
fig, ax = plt.subplots()
ax.fill_between(x, p5, p95, facecolor="lightblue", alpha=0.7)
ax.scatter(x_train, y_train, s=50, fc="none", ec="b", label="train")
ax.plot(x, y, "g", label=r"$\sin(2 \pi x)$")
ax.plot(x, y_pred, "r", label=r"$y(x;\hat{\mathbf{w}})$")
ax.grid()
ax.legend()
plt.show()


コメント