目次
概要
度数分布表とヒストグラムについて解説し、matplotlib でヒストグラムを作成する方法について解説します。
度数分布表
観測値のとり得る値をいくつかの階級 (class) に分け、それぞれの階級で観測値がいくつあるか度数 (frequency)を数えて、表にしたものを度数分布表といいます。度数分布表に関連する用語をいくつか紹介します。
- 階級値 (class value): 階級を代表する値のことを階級値といいます。通常は、階級の上限値と下限値の中間値を階級値とします。
- 相対度数 (relative frequency): 各階級に属する観測値の総数のデータ全体に占める割合のことを相対度数といいます。
- 累積度数 (cumulative frequency): 度数を下の階級から順番に積み上げたときの度数の累積和を累積度数といいます。
- 累積相対度数 (cumulative relative frequency): 相対度数を下の階級から順番に積み上げたときの相対度数の累積和を累積相対度数といいます。
- ヒストグラム (histogram): 各階級の度数を棒グラフで表現したグラフをヒストグラムといいます。
pandas で度数分布表を作成する
200人の試験の得点が記録された観測値の一覧から度数分布表を作成してみます。
In [1]:
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
np.random.seed(0)
scores = pd.Series(np.around(np.random.normal(65, 15, 200).clip(0, 100)))
print(scores)0 91.0
1 71.0
2 80.0
3 99.0
4 93.0
...
195 62.0
196 77.0
197 77.0
198 97.0
199 85.0
Length: 200, dtype: float64
階級に分割し、各階級の度数を集計する処理は pandas.Series.value_counts() で行います。
階級をどのように作成するかは bins で指定します。
- 各階級の端点を表すリストを指定する
- 階級の数を整数で指定する
In [2]:
bins = np.linspace(0, 100, 11)
print(bins)
freq = scores.value_counts(bins=bins, sort=False)
print(freq)[ 0. 10. 20. 30. 40. 50. 60. 70. 80. 90. 100.] (-0.001, 10.0] 0 (10.0, 20.0] 0 (20.0, 30.0] 1 (30.0, 40.0] 4 (40.0, 50.0] 30 (50.0, 60.0] 44 (60.0, 70.0] 41 (70.0, 80.0] 45 (80.0, 90.0] 18 (90.0, 100.0] 17 dtype: int64
階級値、相対度数、累積度数、相対累積度数は次のように計算できます。
In [3]:
class_value = (bins[:-1] + bins[1:]) / 2 # 階級値
rel_freq = freq / scores.count() # 相対度数
cum_freq = freq.cumsum() # 累積度数
rel_cum_freq = rel_freq.cumsum() # 相対累積度数以上を表にまとめて、度数分布表を作成します。
In [4]:
dist = pd.DataFrame(
{
"階級値": class_value,
"度数": freq,
"相対度数": rel_freq,
"累積度数": cum_freq,
"相対累積度数": rel_cum_freq,
},
index=freq.index
)
dist| 階級値 | 度数 | 相対度数 | 累積度数 | 相対累積度数 | |
|---|---|---|---|---|---|
| (-0.001, 10.0] | 5.0 | 0 | 0.000 | 0 | 0.000 |
| (10.0, 20.0] | 15.0 | 0 | 0.000 | 0 | 0.000 |
| (20.0, 30.0] | 25.0 | 1 | 0.005 | 1 | 0.005 |
| (30.0, 40.0] | 35.0 | 4 | 0.020 | 5 | 0.025 |
| (40.0, 50.0] | 45.0 | 30 | 0.150 | 35 | 0.175 |
| (50.0, 60.0] | 55.0 | 44 | 0.220 | 79 | 0.395 |
| (60.0, 70.0] | 65.0 | 41 | 0.205 | 120 | 0.600 |
| (70.0, 80.0] | 75.0 | 45 | 0.225 | 165 | 0.825 |
| (80.0, 90.0] | 85.0 | 18 | 0.090 | 183 | 0.915 |
| (90.0, 100.0] | 95.0 | 17 | 0.085 | 200 | 1.000 |
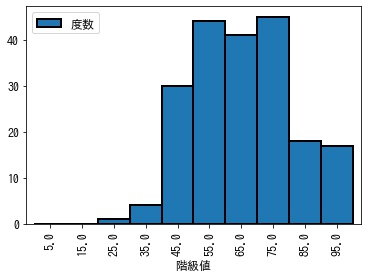
度数分布表からヒストグラムを作成します。
In [5]:
dist.plot.bar(x="階級値", y="度数", width=1, ec="k", lw=2)<matplotlib.axes._subplots.AxesSubplot at 0x7f89b9411df0>
累積相対度数も合わせて描画したい場合は、以下のようにします。
In [6]:
fig, ax1 = plt.subplots()
dist.plot.bar(x="階級値", y="度数", ax=ax1, width=1, ec="k", lw=2)
ax2 = ax1.twinx()
ax2.plot(np.arange(len(dist)), dist["相対累積度数"], "--o", color="k")
ax2.set_ylabel("累積相対度数");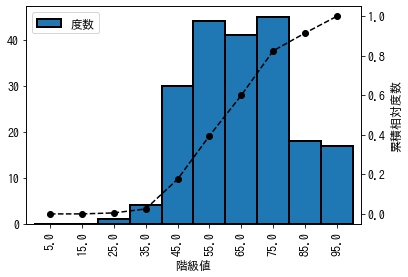
ヒストグラムの種類
峰の数によって、次のように分類できます。
- 単峰型 (unimodal): 峰が1つの分布
- 双峰型 (bimodal): 峰が2つ以上ある分布
双峰型の分布は、性質の異なるデータが混じり合っている場合が多く、グループごとに分布を分けることで単峰型の分布に帰着できる場合があります。この処理を層別といいます。
以下は500人分の性別と身長が記録されたデータで、このデータからヒストグラムを作成します。
In [7]:
import numpy as np
import pandas as pd
np.random.seed(0)
def get_sample():
sex = np.random.choice(["男性", "女性"])
if sex == "男性":
height = np.random.normal(171, 5.7)
else:
height = np.random.normal(157, 5.5)
return sex, height
df = pd.DataFrame([get_sample() for i in range(500)], columns=["性別", "身長"])
df.head()| 性別 | 身長 | |
|---|---|---|
| 0 | 男性 | 177.399931 |
| 1 | 女性 | 158.665429 |
| 2 | 女性 | 159.036405 |
| 3 | 男性 | 176.931025 |
| 4 | 男性 | 169.339054 |
In [8]:
ret = df.hist(bins=20, ec="k", lw=2, grid=False)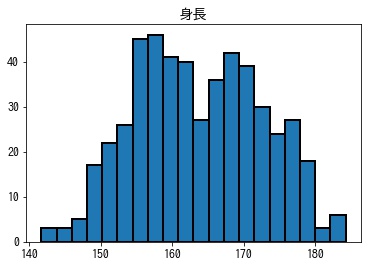
2つの峰がある双峰型の分布であることがわかります。次に男性、女性で性別ごとに分けて、ヒストグラムを作成します。
In [9]:
df[df["性別"] == "男性"].hist(bins=20, ec="k", lw=2, grid=False)
df[df["性別"] == "女性"].hist(bins=20, ec="k", lw=2, grid=False)array([[<matplotlib.axes._subplots.AxesSubplot object at 0x7f89b9ddfdc0>]],
dtype=object)

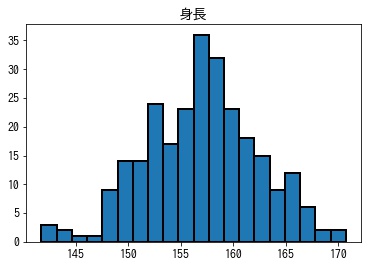
層別を行い、グループごとに分けてヒストグラムを作成したことで、峰が1つの単峰型の分布になりました。


コメント