Warning: Undefined variable $position in /home/pystyles/pystyle.info/public_html/wp/wp-content/themes/lionblog/functions.php on line 4897
  1. HOME
  2. 数学
  3. 統計学 - 超幾何分布

統計学 – 超幾何分布

統計学 – 超幾何分布
目次

概要

離散確率分布の1つである超幾何分布について解説します。

Advertisement

確率関数

確率変数 $X$ が次のような確率関数をもつとき、$X$ はパラメータ $N, k, n$ の超幾何分布 (hypergeometric distribution) に従うという。

$$ f_X(x) = \begin{cases} \frac{\binom{K}{x} \binom{N – K}{n – x}}{\binom{N}{n}} & n = 0, 1, \cdots, n \\ 0 & その他の場合 \end{cases} $$

ただし、$N \in \{0, 1, \cdots\}, K \in \{0, 1, \cdots, N\}, n \in \{0, 1, \cdots, N\}, N \ge K, N \ge n$ とする。

確率関数である

$$ \begin{aligned} \sum_{x = 0}^n \frac{\binom{K}{x} \binom{N – K}{n – x}}{\binom{N}{n}} &= \frac{\binom{N}{n}}{\binom{N}{n}} \quad \because \sum_{x = 0}^n \binom{K}{x} \binom{N – K}{n – x} = \binom{N}{n} \\ &= 1 \end{aligned} $$

期待値

$$ \begin{aligned} E[X] &= \sum_{x = 0}^n x \frac{\binom{K}{x} \binom{N – K}{n – x}}{\binom{N}{n}} \\ &= \sum_{x = 1}^n x \frac{\binom{K}{x} \binom{N – K}{n – x}}{\binom{N}{n}} \quad \because 第0項は0 \\ &= \sum_{x = 0}^n x \frac{K}{x} \frac{n}{N} \frac{\binom{K – 1}{x – 1} \binom{N – K}{n – x}}{\binom{N – 1}{n – 1}} \quad \because \binom{a}{b} = \frac{a}{b} \binom{a – 1}{b – 1} \\ &= n \frac{K}{N} \sum_{x = 1}^n \frac{\binom{K – 1}{x – 1} \binom{N – K}{n – x}}{\binom{N – 1}{n – 1}} \\ &= n \frac{K}{N} \sum_{x = 0}^n f_X(x) \quad \because パラメータ N – 1, K – 1, n – 1 の超幾何分布 \\ &= n \frac{K}{N} \\ \end{aligned} $$

分散

$$ \begin{aligned} E[X(X – 1)] &= \sum_{x = 0}^n x (x – 1) \frac{\binom{K}{x} \binom{N – K}{n – x}}{\binom{N}{n}} \\ &= \sum_{x = 2}^n x (x – 1) \frac{\binom{K}{x} \binom{N – K}{n – x}}{\binom{N}{n}} \quad \because 第0項、第1項は0 \\ &= \sum_{x = 2}^n x (x – 1) \frac{K}{x} \frac{K – 1}{x – 1} \frac{n}{N} \frac{n – 1}{N – 1} \frac{\binom{K – 2}{x – 2} \binom{N – K}{n – x}}{\binom{N – 2}{n – 2}} \quad \because \binom{a}{b} = \frac{a}{b} \binom{a – 1}{b – 1} \\ &= n (n – 1) \frac{K (K – 1)}{N (N – 1)} \sum_{x = 2}^n \frac{\binom{K – 2}{x – 2} \binom{N – K}{n – x}}{\binom{N – 2}{n – 2}} \\ &= n (n – 1) \frac{K (K – 1)}{N (N – 1)} \sum_{x = 0}^n f_X(x) \quad \because パラメータ N – 2, K – 2, n – 2 の超幾何分布 \\ &= n (n – 1) \frac{K (K – 1)}{N (N – 1)} \\ \end{aligned} $$

よって、分散は

$$ \begin{aligned} Var[X] &= E[X^2] – [E(X)]^2 \\ &= E[X(X – 1)] + E[X] – [E(X)]^2 \\ &= n (n – 1) \frac{K (K – 1)}{N (N – 1)} + n \frac{K}{N} – \left( n \frac{K}{N} \right)^2 \\ &= n K \frac{N^2 + nK – nN – KN}{N^2 (N – 1)} \\ &= \frac{n K (N – K)(N – n)}{N^2 (N – 1)} \\ \end{aligned} $$
Advertisement

標準偏差

$$ Std(X) = \sqrt{Var(X)} = \left( \frac{n K (N – K)(N – n)}{N^2 (N – 1)} \right)^\frac{1}{2} $$

scipy.stats の超幾何分布

scipy.stats.hypergeom で超幾何分布に従う確率変数を作成できます。

In [1]: 
import numpy as np
import seaborn as sns
from matplotlib import pyplot as plt
from scipy.stats import hypergeom

sns.set(style="white")

X = hypergeom(20, 7, 12)

サンプリング

In [2]: 
x = X.rvs(size=10)
print(x)
[4 5 2 3 4 6 5 6 3 4]

確率質量関数

In [3]: 
x = np.arange(0, 20)
y = X.pmf(x)

fig, ax = plt.subplots()
ax.stem(x, y, use_line_collection=True)
ax.grid()

plt.show()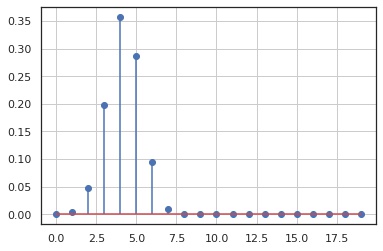
Advertisement

累積分布関数

In [4]: 
x = np.arange(0, 20)
y = X.cdf(x)

fig, ax = plt.subplots()
ax.step(x, y)
ax.grid()

plt.show()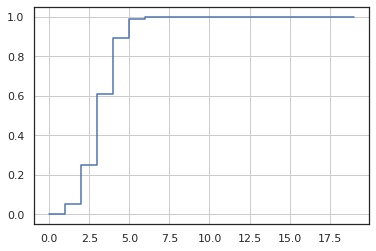

統計量

In [5]: 
print("mean", X.mean())
print("var", X.var())
print("std", X.std())
mean 4.199999999999999
var 1.1494736842105264
std 1.0721351053904198