概要
最尤推定 (Maximum Likelihood Estimation / MLE) について、Python で動かしながら理解することを目的とした記事になります。
尤度関数
$\mathbf{X} = (X_1, X_2, \cdots, X_N)$ がランダム標本の場合、
$$ L(\mathbf{\theta};\mathbf{x}) = f(\mathbf{x};\mathbf{\theta}) = \prod_{i = 1}^N f(x_i;\mathbf{\theta}) $$ただし、$f(x_i;\mathbf{\theta})$ は母集団分布の確率関数または確率密度関数です。
尤度関数は、パラメータ $\mathbf{\theta}$ のとき、得られた観測値 $\mathbf{x}$ の出やすさを表していると解釈できます。
- 入門・演習 数理統計 (6.3 最尤推定)
- 尤度関数 – Wikipedia
例 正規分布の尤度関数
母集団分布が標準正規分布であるランダム標本から、観測値 $\mathbf{x} = (\mathbf{x}_1, \cdots, \mathbf{x}_N)$ が得られたとき、その尤度関数は
$$ \begin{aligned} L(\mathbf{\theta};\mathbf{x}) &= f(\mathbf{x};\mathbf{\theta}) \\ &= \prod_{i = 1}^N f(x_i;\mathbf{\theta}) \\ &= \prod_{i = 1}^N \frac{1}{\sqrt{2 \pi \sigma^2}}\exp \left(-\frac{(x_i – \mu)^2}{2 \sigma^2} \right) \end{aligned} $$となります。Python で計算してみます。
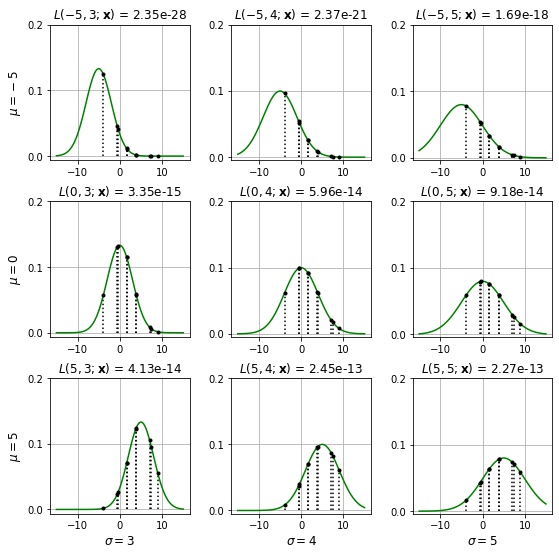
- $\mu=0, \sigma=4$ の正規分布に従う大きさ10のランダム標本の観測値を得て、$(\mu, \sigma) \in {\{-5, 0, 5\} \times \{3, 4, 5\}}$ のときの尤度関数 $L(\mu, \sigma; \mathbf{x})$ の値を計算します。
- 平均
mu、標準偏差sigmaの正規分布の確率密度関数は、scipy.stats.norm.pdf(x, loc=mu, scale=sigma) で計算できます。 - 尤度関数の値は、$x_i$ の確率密度関数の値 $f(x_i;\mathbf{\theta})$ の総乗を取ればよいので、numpy.prod() で計算します。
from itertools import product
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm
np.random.seed(0)
def likelihood(mu, sigma, x):
# μ=mu, σ=sigma の正規分布の結合確率密度関数の値を計算する
return norm.pdf(x, loc=mu, scale=sigma).prod()
# 母集団分布が μ=0, σ=4 の正規分布であるとき、大きさ10のランダム標本の観測値を得る。
x = norm.rvs(0, 4, size=10)
print(x)
fig = plt.figure(figsize=(9, 9))
fig.subplots_adjust(wspace=0.3, hspace=0.3)
for i, (mu, sigma) in enumerate(product([-5, 0, 5], [3, 4, 5])):
ax = fig.add_subplot(3, 3, i + 1)
# μ=mu, σ=sigma の正規分布の確率密度関数を描画する
xs = np.linspace(-15, 15, 100)
ys = norm.pdf(xs, loc=mu, scale=sigma)
ax.plot(xs, ys, "g")
# ランダム標本の観測値を描画する。
y = norm.pdf(x, loc=mu, scale=sigma)
markerline, stemline, baseline = ax.stem(
x, y, linefmt="k:", markerfmt="ko", basefmt="none", use_line_collection=True
)
plt.setp(markerline, ms=3)
l = likelihood(mu, sigma, x)
ax.set_title(fr"$L({mu}, {sigma};\mathbf{{x}})$ = {l:.2e}")
ax.set_xticks([-10, 0, 10])
ax.set_yticks([0.0, 0.1, 0.2])
ax.grid()
if i % 3 == 0:
ax.set_ylabel(fr"$\mu = {mu}$", fontsize=12)
if i // 3 == 2:
ax.set_xlabel(fr"$\sigma = {sigma}$", fontsize=12)
plt.show()[ 7.05620938 1.60062883 3.91495194 8.9635728 7.47023196 -3.90911152 3.80035367 -0.60542883 -0.41287541 1.64239401]
最尤推定
尤度関数を最大にするパラメータ $\hat{\mathbf{\theta}} = \underset{\mathbf{\theta}}{\operatorname{argmax}} L(\mathbf{\theta};\mathbf{x})$ を 最尤推定値 (maximum likelihood estimate) といいます。最尤推定値は $\mathbf{x}$ によって決まるので、$\mathbf{x}$ の関数 $\hat{\mathbf{\theta}}(\mathbf{x})$ となります。 また、$\theta(X)$ を最尤推定量 (maximum likelihood estimator) といいます。パラメータの推定に最尤推定量を採用する方法を最尤推定法 といいます。 尤度関数 $L(\mathbf{\theta};\mathbf{x})$ は、パラメータ $\mathbf{\theta}$ のときの観測値 $\mathbf{x}$ の出やすさを表しているので、最尤推定法はその観測値が尤も出やすいパラメータを求めることにほかなりません。
- 入門・演習 数理統計 (6.3 最尤推定)
- 最尤推定 – Wikipedia
対数尤度関数
尤度関数の対数をとった $\log L(\mathbf{\theta};\mathbf{x})$ を対数尤度関数 (log likelihood function) といいます。対数関数は増加関数なので、$L(\mathbf{\theta};\mathbf{x})$ を最大にする $\hat{\mathbf{\theta}}$ は、$\log L(\mathbf{\theta};\mathbf{x})$ も最大にします。
対数をとることで、尤度関数の総乗は総和になります。
$$ \begin{aligned} \log L(\mathbf{\theta};\mathbf{x}) &= \log \prod_{i = 1}^N f(x_i;\mathbf{\theta}) \\ &= \sum_{i = 1}^N \log f(x_i;\mathbf{\theta}) \end{aligned} $$- 入門・演習 数理統計 (6.3 最尤推定)
横軸に尤度関数、縦軸に対数尤度関数をとるグラフを描画します。
fig, ax = plt.subplots()
x = np.linspace(0.01, 1, 100)
y = np.log(x)
ax.plot(x, y)
ax.grid()
ax.set_xlabel(r"$L(\mathbf{\theta};\mathbf{x})$")
ax.set_ylabel(r"$\log L(\mathbf{\theta};\mathbf{x})$")
plt.show()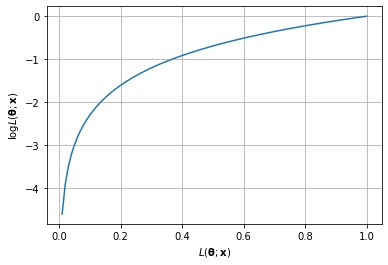
対数尤度方程式
パラメータ空間 $\Theta$ で定義される微分可能な尤度関数 $L(\mathbf{\theta};\mathbf{x})$ が凹関数であるとき、尤度関数を最大にする $\hat{\mathbf{\theta}}$ は、
$$ \nabla L(\hat{\mathbf{\theta}};\mathbf{x}) = \mathbf{0} $$を満たします。これを尤度方程式といいます。
$L(\mathbf{\theta};\mathbf{x})$ を最大にする $\hat{\mathbf{\theta}}$ は、$\log L(\mathbf{\theta};\mathbf{x})$ も最大にするので、
$$ \nabla \log L(\hat{\mathbf{\theta}};\mathbf{x}) = \mathbf{0} $$も同時に満たします。こちらは対数尤度方程式といいます。
- 入門・演習 数理統計 (6.3 最尤推定)
例: ベルヌーイ分布の最尤推定
パラメータ $p$ のベルヌーイ分布の確率関数は以下になります。
$$ f(x) = p^x (1 – p)^{1 – x}, x = 0, 1 $$母集団分布がパラメータ $p$ のベルヌーイ分布であるランダム標本から、観測値 $\mathbf{x} = (x_1, x_2, \cdots, x_N)$ が得られたとき、その対数尤度関数は
$$ \begin{aligned} \log L(p;\mathbf{x}) &= \sum_{i = 1}^N \log f(x_i;p) \\ &= \left( \sum_{i = 1}^N x_i \right) \log p + \left( N – \sum_{i = 1}^N x_i \right) \log (1 – p) \\ \end{aligned} $$ベルヌーイ分布の尤度関数は、凹関数なので、対数尤度方程式を解けば解が求まります。(証明略)
$$ \begin{aligned} \frac{d}{dp} \log L(p;\mathbf{x}) = \frac{\sum_{i = 1}^N x_i}{p} – \frac{N – \sum_{i = 1}^N x_i}{1 – p} &= 0 \end{aligned} $$これを解くと、
$$ \hat{p} = \frac{1}{N} \sum_{i = 1}^N x_i $$となり、$p$ の最尤推定値は標本平均であることがわかりました。
Python でベルヌーイ分布の最尤推定を試してみます。
- 母集団分布がパラメータ $p = 0.3$ のベルヌーイ分布である大きさ50のランダム標本から、観測値を取得します。
- ベルヌーイ分布は scipy.stats.bernoulli で扱います。
import numpy as np
from scipy.stats import bernoulli
np.random.seed(0)
# 母集団分布が p=0.3 の正ベルヌーイ分布であるとき、大きさ50のランダム標本の観測値を得る。
p = 0.3
x = bernoulli.rvs(p, size=50)
print(x)
# 最尤推定値を計算する。
p_pred = x.mean()
print(p_pred)[0 1 0 0 0 0 0 1 1 0 1 0 0 1 0 0 0 1 1 1 1 1 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0] 0.28
真のパラメータ $p = 0.3$ に対して、推定したパラメータは $p = 0.28$ となりました。 サンプル数を変化させた場合の推定値を確認してみます。
np.random.seed(0)
for n in np.geomspace(1, 10000000, 8, dtype=int):
# 母集団分布が p=0.3 の正ベルヌーイ分布であるとき、大きさnのランダム標本の観測値を得る。
x = bernoulli.rvs(0.3, size=n)
# 最尤推定値を計算する。
p_pred = x.mean()
print(f"N={n:<8} p={p_pred:.6f}")N=1 p=0.000000 N=10 p=0.400000 N=100 p=0.220000 N=1000 p=0.300000 N=10000 p=0.295900 N=100000 p=0.301270 N=1000000 p=0.300599 N=10000000 p=0.300029
サンプル数を増やしたことで、推定値が真のパラメータ $p=0.3$ に近くなることが確認できました。
例: 正規分布の最尤推定
パラメータ $\mu, \theta$ の正規分布の確率関数は以下になります。
$$ f(x) = \prod_{i = 1}^N \frac{1}{\sqrt{2 \pi \sigma^2}}\exp \left(-\frac{(x – \mu)^2}{2 \sigma^2} \right) $$正規分布のランダム標本から観測値 $\mathbf{x} = (\mathbf{x}_1, \cdots, \mathbf{x}_N)$ が得られたとき、その対数尤度関数は
$$ \begin{aligned} \log L(\mu, \sigma^2;\mathbf{x}) &= \sum_{i = 1}^N \log f(x_i;p) \\ &= \sum_{i = 1}^N – \frac{1}{2} \log (2 \pi \sigma^2) – \frac{1}{2 \sigma^2} \sum_{i = 1}^N (x_i – \mu)^2 \\ &= – \frac{N}{2} \log (2 \pi) – \frac{N}{2} \log \sigma^2 – \frac{1}{2 \sigma^2} \sum_{i = 1}^N (x_i – \mu)^2\\ \end{aligned} $$正規分布の尤度関数は、凹関数なので、対数尤度方程式を解けば解が求まります。(証明略)
$$ \begin{aligned} \frac{d}{d\mu} \log L(\mu, \sigma^2;\mathbf{x}) &= \frac{1}{\sigma^2} \sum_{i = 1}^N (x_i – \mu) = 0 \\ \frac{d}{d\sigma^2} \log L(\mu, \sigma^2;\mathbf{x}) &= – \frac{n}{2 \sigma^2} + \frac{1}{2 \sigma^4} \sum_{i = 1}^N (x_i – \mu)^2 = 0 \end{aligned} $$これを解くと、
$$ \begin{aligned} \hat{\mu} &= \frac{1}{N} \sum_{i = 1}^N x_i \\ \hat{\sigma}^2 &= \frac{1}{N} \sum_{i = 1}^N \left( x_i – \frac{1}{N} \sum_{i = 1}^N x_i \right)^2 = \frac{1}{N} \sum_{i = 1}^N (x_i – \hat{\mu})^2 \end{aligned} $$となり、最尤推定値は $\mu$ が標本平均、$\sigma^2$ が標本分散となることがわかりました。
正規分布の尤度関数を可視化する
パラメータ空間 $\Theta = \{(\mu, \sigma); \mu \in \mathbb{R}, \sigma \in [0, \infty)\}$ 上で定義される正規分布の尤度関数 $L(\mu, \sigma;\mathbf{x})$ を描画します。
- numpy.mgrid でパラメータ空間 $\Theta$ 上に格子状の点を作成する。
- 各点における尤度関数の値を計算する。
- Axes3D.plot_wireframe() で尤度関数のグラフを描画する。
- matplotlib.pyplot.contour() で尤度関数の等高線を描画する。
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm
np.random.seed(0)
def likehood(x, mu, sigma):
return np.prod(norm.pdf(x, loc=mu, scale=sigma))
# 集団分布が平均0、標準偏差40の正規分布であるとき、大きさ100のランダム標本の観測値を得る。
mu, sigma = 0, 40
x = norm.rvs(loc=mu, scale=sigma, size=100) # size を増やしすぎると、float で表せなくなります。
# 各点の尤度関数の値を計算する。
X, Y = np.mgrid[-10:10:30j, 20:60:30j]
Z = []
for m, t in zip(X.ravel(), Y.ravel()):
Z.append(likehood(x, mu=m, sigma=t))
Z = np.array(Z).reshape(*X.shape)
# 最尤推定量を計算する。
mu_pred, sigma_pred = x.mean(), x.std()
fig = plt.figure(figsize=(12, 6))
# 3D グラフを描画する。
ax1 = fig.add_subplot(121, projection="3d")
ax1.plot_wireframe(X, Y, Z)
ax1.set_xlabel(r"$\mu$", fontsize=15)
ax1.set_ylabel(r"$\sigma$", fontsize=15)
# 等高線を描画する。
ax2 = fig.add_subplot(122)
ax2.contour(X, Y, Z)
ax2.scatter(mu, sigma, c="g", label=fr"True: $\mu$={mu:.2f}, $\sigma$={sigma:.2f}")
ax2.scatter(
mu_pred,
sigma_pred,
c="r",
label=fr"Estimation: $\mu$={mu_pred:.2f}, $\sigma$={sigma_pred:.2f}",
)
ax2.set_xlabel(r"$\mu$", fontsize=15)
ax2.set_ylabel(r"$\sigma$", fontsize=15)
ax2.grid()
ax2.legend()
plt.show()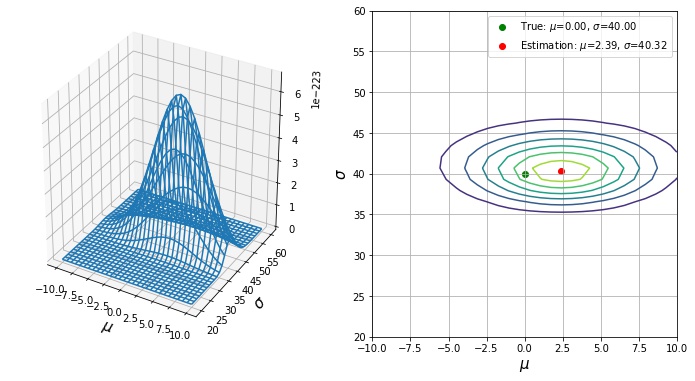
真のパラメータ $\mu=0, \sigma=40$ に対して、推定値 $\hat{\mu}=2.39, \hat{\sigma}=40.32$ なので、それなりに推定できていることが確認できます。


コメント