Warning: Undefined variable $position in /home/pystyles/pystyle.info/public_html/wp/wp-content/themes/lionblog/functions.php on line 4897
  1. HOME
  2. 数学
  3. 統計学 - 負の二項分布

統計学 – 負の二項分布

統計学 – 負の二項分布
目次

概要

離散確率分布の1つである負の二項分布について解説します。

Advertisement

確率関数

確率変数 $X$ が次のような確率関数をもつとき、$X$ はパラメータ $r, p$ の負の二項分布 (negative binominal distribution) に従うという。

$$ f_X(x) = \begin{cases} \binom{x + r – 1}{x} p^r (1 – p)^x & x = 0, 1, \cdots \\ 0 & その他の場合 \end{cases} $$

ただし、$r$ は正の整数、$0 < p < 1$

確率関数である

$$ \begin{aligned} &\sum_{x = 0}^\infty \binom{x + r – 1}{x} p^r (1 – p)^x \\ &= p^r \sum_{x = 0}^\infty \binom{-r}{x} (p – 1)^x \quad \because \binom{x + r – 1}{x} = \binom{-r}{x} (-1)^x \\ &= p^r p^{-r} \quad \because |p – 1| < 1 より、二項展開 \\ &= 1 \\ \end{aligned} $$

また、$f_X(x) \ge 0$ は明らか。

解釈

結果が成功か失敗かのいずれかである試行をベルヌーイ試行 (Bernoulli trial) という。 $r$ 回失敗するまでベルヌーイ試行を続けた場合の成功回数の分布はパラメータ $r, p$ の負の二項分布に従う。

累積確率関数

$$ P(X \le x) = \sum_{k = 0}^{\lfloor x \rfloor} \binom{x + r – 1}{x} p^r (1 – p)^x $$

aludaatAMS9-12-2018.pdf

Advertisement

期待値

$$ \begin{aligned} E[X] &= \sum_{x = 0}^\infty x \binom{x + r – 1}{x} p^r (1 – p)^x \\ &= \sum_{x = 0}^\infty x \frac{(x + r – 1)!}{(r – 1)!x!} p^r (1 – p)^x \\ &= \sum_{x = 1}^\infty x \frac{(x + r – 1)!}{(r – 1)!x!} p^r (1 – p)^x \quad \because 第0項は0 \\ &= \sum_{x = 1}^\infty \frac{(x + r – 1)!}{(r – 1)!(x – 1)!} p^r (1 – p)^x \end{aligned} $$

ここで、$x’ = x – 1, r’ = r + 1$ とおくと、

$$ \begin{aligned} E[X] &= \sum_{x’ = 0}^\infty \frac{(x’ + r’ – 1)!}{(r’ – 2)! x’!} p^{r’ – 1} (1 – p)^{x’ + 1} \\ &= \frac{1 – p}{p} (r’ – 1) \sum_{x’ = 0}^\infty \frac{(x’ + r’ – 1)!}{(r’ – 1)! x’!} p^{r’} (1 – p)^{x’} \\ &= \frac{1 – p}{p} (r’ – 1) \quad \because パラメータ r’, p の負の二項分布の総和は1 \\ &= \frac{1 – p}{p} r \quad \because r’ = r + 1 \end{aligned} $$

分散

$$ \begin{aligned} E[X(X – 1)] &= \sum_{x = 0}^\infty x(x – 1) \binom{x + r – 1}{x} p^r (1 – p)^x \\ &= \sum_{x = 0}^\infty x(x – 1) \frac{(x + r – 1)!}{(r – 1)!x!} p^r (1 – p)^x \\ &= \sum_{x = 1}^\infty x(x – 1) \frac{(x + r – 1)!}{(r – 1)!x!} p^r (1 – p)^x \quad \because 第0項は0 \\ &= \sum_{x = 1}^\infty \frac{(x + r – 1)!}{(r – 1)!(x – 2)!} p^r (1 – p)^x \end{aligned} $$

ここで、$x’ = x – 2, r’ = r + 2$ とおくと、

$$ \begin{aligned} E[X(X – 1)] &= \sum_{x’ = 0}^\infty \frac{(x’ + r’ – 1)!}{(r’ – 3)! x’!} p^{r’ – 2} (1 – p)^{x’ + 2} \\ &= \frac{(1 – p)^2}{p^2} (r’ – 1) (r’ – 2) \sum_{x’ = 0}^\infty \frac{(x’ + r’ – 1)!}{(r’ – 1)! x’!} p^{r’} (1 – p)^{x’} \\ &= \frac{(1 – p)^2}{p^2} (r’ – 1) (r’ – 2) \quad \because パラメータ r’, p の負の二項分布の総和は1 \\ &= \frac{(1 – p)^2}{p^2} r(r + 1) \quad \because r’ = r + 2 \end{aligned} $$

よって、分散は

$$ \begin{aligned} Var[X] &= E[X^2] – [E(X)]^2 \\ &= E[X(X – 1)] + E[X] – [E(X)]^2 \\ &= \frac{(1 – p)^2}{p^2} r(r + 1) + \frac{1 – p}{p} r – \left( \frac{1 – p}{p} r \right)^2 \\ &= \frac{1 – p}{p^2} \end{aligned} $$

積率母関数

$$ \begin{aligned} m_X(t) &= E[e^{tX}] \\ &= \sum_{x = 0}^\infty e^{tx} \binom{x + r – 1}{x} p^r (1 – p)^x \\ &= \sum_{x = 0}^\infty e^{tx} \binom{-r}{x} (-1)^x p^r (1 – p)^x \quad \because \binom{x + r – 1}{x} = \binom{-r}{x} (-1)^x \\ &= \sum_{x = 0}^\infty \binom{-r}{x} p^r [-e^{t} (1 – p)]^x \end{aligned} $$

$|-e^{t} (1 – p)| < 1$、つまり、$0 < e^{t} (1 – p) < 1$ のとき、二項展開より、

$$ \begin{aligned} \sum_{x = 0}^\infty \binom{-r}{x} p^r [-e^{t} (1 – p)]^x &= p^r (1 – (1 – p) e^t)^{-r} &= \left( \frac{p}{1 – (1 – p) e^t} \right)^r \end{aligned} $$

再生性

$X_1, X_2, \cdots, X_n$ が独立でそれぞれパラメータ $r_i, p$ の負の二項分布に従うとき、 $S = X_1 + X_2 + \cdots + X_n$ はパラメータ $r_1 + r_2 + \cdots + r_n, p$ の負の二項分布に従う。

証明:

$X_i$ の積率母関数を $m_{X_i}(t)$ とすると、

$$ \begin{aligned} m_S(t) &= \prod_{i = 1}^n m_{X_i}(t) \\ &= \prod_{i = 1}^n \left( \frac{p}{1 – (1 – p) e^t} \right)^{n r_i} \\ &= \left( \frac{p}{1 – (1 – p) e^t} \right)^{n \sum_{i = 1}^n r_i} \\ \end{aligned} $$

これはパラメータ $r_1 + r_2 + \cdots + r_n, p$ の負の二項分布の積率母関数と一致する。 積率母関数の一意性より、題意は示された。

Advertisement

scipy.stats の二項分布

scipy.stats.nbinom で二項分布に従う確率変数を作成できます。

In [1]: 
import numpy as np
import seaborn as sns
from matplotlib import pyplot as plt
from scipy.stats import nbinom

sns.set(style="white")

X = nbinom(n=5, p=0.5)

サンプリング

In [2]: 
x = X.rvs(size=10)
print(x)
[ 3  8  9  6 11  4  7  2  5  2]

確率質量関数

In [3]: 
x = np.arange(0, 20)
y = X.pmf(x)

fig, ax = plt.subplots()
ax.stem(x, y, use_line_collection=True)
ax.grid()

plt.show()

累積分布関数

In [4]: 
x = np.arange(0, 20)
y = X.cdf(x)

fig, ax = plt.subplots()
ax.step(x, y)
ax.grid()

plt.show()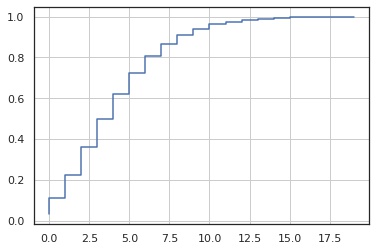
Advertisement

統計量

In [5]: 
print("mean", X.mean())
print("var", X.var())
print("std", X.std())
mean 5.0
var 10.0
std 3.1622776601683795