概要
物体検出モデルの精度評価には、mean Average Precision (mAP) が使われます。 今回はこの mAP について、実装例を示しながら、解説します。
矩形の座標の表現方法
矩形の座標の表現方法には、PASCAL VOC データセットのように左上及び右下の $(x, y)$ 座標で表す形式と COCO データセットのように左上の $(x, y)$ 座標及び幅、高さで表す形式があります。
Intersection Over Union (IOU)
mAP の計算では、2つの矩形がどのくらい重なっているかを表す指標 Intersection Over Union (IOU) が使われます。 2つの矩形 $A, B$ が与えられたとき、その IOU は、共通部分の面積 $\text{area}(A \cap B)$ を和集合の面積 $\text{area}(A \cup B)$ で割ることで計算できます。
$$ \mathrm{IOU} = \frac{\mathrm{area}(A \cap B)}{\mathrm{area}(A \cup B)} $$
式からわかるように IOU は $[0, 1]$ の値をとり、完全に重なっている場合は1、全く重なっていない場合は0になります。
物体検出における TP、FP、FN
mAP の計算では、検出した矩形が正解かどうかをまず判定します。
ある画像に対する ground truth (正解データのこと) の矩形、検出した矩形が以下のようであったとします。
| Xmin | Ymin | Xmax | Ymax | |
|---|---|---|---|---|
| a | 50 | 50 | 200 | 200 |
| b | 250 | 100 | 350 | 300 |
ground truth の矩形
| Score | Xmin | Ymin | Xmax | Ymax | |
|---|---|---|---|---|---|
| c | 0.8 | 45 | 45 | 180 | 210 |
| d | 0.9 | 80 | 40 | 220 | 180 |
| e | 0.5 | 260 | 200 | 340 | 310 |
検出した矩形
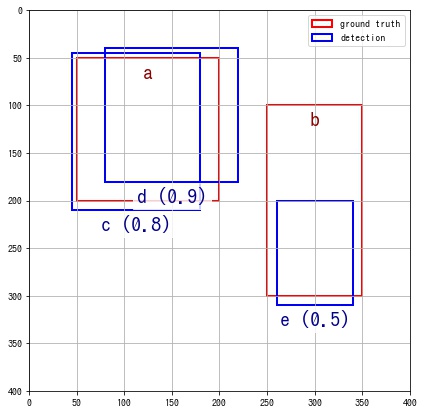
ground truth の矩形 a, b と検出した矩形 c, d, e との IOU をそれぞれ計算すると以下のとおりになります。
| c | d | e | |
|---|---|---|---|
| a | 0.77 | 0.59 | 0 |
| b | 0 | 0 | 0.39 |
検出した矩形が正解かどうかは、その矩形との IOU が最大の ground truth の矩形が、「IOU が閾値以上」かつ「まだ他の検出した矩形と紐付いていない」かどうかで判定します。 判定はスコアが高い検出した矩形から行っていきます。
IOU の閾値は今回、0.5とします。スコアが高い順なので、d, c, e の順で判定します。
- 矩形
dと一番 IOU が高い ground truth の矩形はaです。 「iou(d, a) = 0.59 なので閾値以上」かつ「まだ他の検出した矩形と紐付いていない」ので、矩形dは正解とします。 - 矩形
cと一番 IOU が高い ground truth の矩形はaです。 「iou(c, a) = 0.77 なので閾値以上」ではあるが、「矩形aはすでに矩形dと紐付いている」ので、矩形cは不正解とします。 - 矩形
eと一番 IOU が高い ground truth の矩形はbです。 「iou(e, b) = 0.39 なので閾値未満」であるから、矩形eは不正解とします。
よって、この画像の検出した矩形が正解かどうかは以下のようになります。
| 正解かどうか | |
|---|---|
| c | 不正解 |
| d | 正解 |
| e | 不正解 |
上記の判定結果を使い、物体検出における True Positive、False Positive、False Negative は以下のように定義されます。
- True Positive (TP): 正解した矩形
- False Positive (FP): 正解でない矩形
- False Negative (FN): どの検出した矩形とも紐付いていない ground truth の矩形
物体検出の場合、検出しないのが正解である矩形というのは多数考えられるため、True Negative (TN) は定義されません。
PR 曲線 (precision recall curve)
画像ごとに検出した矩形が正解かどうかを判定したら、以下の表のようになったとします。 なお、検出結果はスコアが高い順にソートされています。
from io import StringIO
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
csv = """Filename,Label,Score,Xmin,Ymin,Xmax,Ymax,Correct
7.png,person,0.95,33.0,116.0,70.0,165.0,True
5.png,person,0.95,29.0,131.0,101.0,160.0,True
3.png,person,0.91,105.0,131.0,152.0,178.0,False
1.png,person,0.88,5.0,67.0,36.0,115.0,True
6.png,person,0.84,17.0,155.0,46.0,190.0,True
1.png,person,0.8,124.0,9.0,173.0,76.0,False
4.png,person,0.78,28.0,68.0,70.0,135.0,True
2.png,person,0.74,19.0,18.0,62.0,53.0,False
2.png,person,0.71,64.0,111.0,128.0,169.0,True
1.png,person,0.7,119.0,111.0,159.0,178.0,True
"""
det_bboxes = pd.read_csv(StringIO(csv))
det_bboxes| Filename | Label | Score | Xmin | Ymin | Xmax | Ymax | Correct | |
|---|---|---|---|---|---|---|---|---|
| 0 | 7.png | person | 0.95 | 33.0 | 116.0 | 70.0 | 165.0 | True |
| 1 | 5.png | person | 0.95 | 29.0 | 131.0 | 101.0 | 160.0 | True |
| 2 | 3.png | person | 0.91 | 105.0 | 131.0 | 152.0 | 178.0 | False |
| 3 | 1.png | person | 0.88 | 5.0 | 67.0 | 36.0 | 115.0 | True |
| 4 | 6.png | person | 0.84 | 17.0 | 155.0 | 46.0 | 190.0 | True |
| 5 | 1.png | person | 0.80 | 124.0 | 9.0 | 173.0 | 76.0 | False |
| 6 | 4.png | person | 0.78 | 28.0 | 68.0 | 70.0 | 135.0 | True |
| 7 | 2.png | person | 0.74 | 19.0 | 18.0 | 62.0 | 53.0 | False |
| 8 | 2.png | person | 0.71 | 64.0 | 111.0 | 128.0 | 169.0 | True |
| 9 | 1.png | person | 0.70 | 119.0 | 111.0 | 159.0 | 178.0 | True |
正解した矩形は True Positive (TP)、不正解だった矩形は False Positive (FP) となり、検出した矩形一覧はスコアが高い順にソート済みなので、累積和をとることで、そのスコアを閾値とした場合の TP、FP の合計が算出できます。
TP = det_bboxes["Correct"]
FP = ~det_bboxes["Correct"]
acc_TP = TP.cumsum()
acc_FP = FP.cumsum()TP、FP が計算できたので、各閾値での Precision と Recall を計算します。 $TP + FN$ は、ground truth の矩形の数になります。
$$ \mathrm{Precision} = \frac{TP}{TP + FP} $$$$ \mathrm{Recall} = \frac{TP}{TP + FN} $$n_positives = 9 # ground truth の矩形の数は9個だったとする。
precision = acc_TP / (acc_TP + acc_FP)
recall = acc_TP / n_positives各閾値での Precision と Recall が計算できたので、PR 曲線を作成します。
fig, ax = plt.subplots()
ax.set_xlim(-0.05, 1.1)
ax.set_ylim(-0.05, 1.1)
ax.grid()
ax.set_title("PR curve")
ax.set_xlabel("Recall")
ax.set_ylabel("Presicion")
ax.plot(recall, precision, "bo-", label="original")
ax.legend()
plt.show()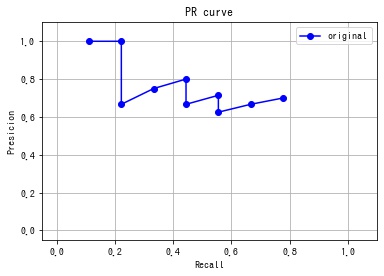
Average Precision (AP) を計算する
次に Average Precision (AP) を計算します。
Recall が $r$ のときの Precision の値を $P(r)$ とします。 Average Precision は、Recall のとり得る範囲 $[0, 1]$ での $P(r)$ の平均 (average) として定義されます。
$$ \mathrm{AP} = \frac{1}{1 – 0} \int_0^1 P(r) dr = \int_0^1 P(r) dr $$実際は、離散的なデータしかないため、以下の手順で PR 曲線を修正したのち、矩形で近似して求めることになります。
まず、Recall の範囲が [0, 1] となるように、(0, 0), (1, 0) の2点 (下図の赤点) を挿入します。
numpy.concatenate() で1次元配列の前後に要素を1つずつ挿入します。
modified_recall = np.concatenate([[0], recall, [1]])
modified_precision = np.concatenate([[0], precision, [0]])
次に Precision が単調減少になるように Recall=1 の点から累積的な最大値をとるように Precision の値を修正します。
この計算には、numpy.maximum.accumulate() を使用します。
# 末尾から累積最大値を計算する。
# [::-1] で前後を逆にして、先頭から累積的な最大値を求めたあと、再度 [::-1] として元の順番に戻している。
modified_precision2 = np.maximum.accumulate(modified_precision[::-1])[::-1]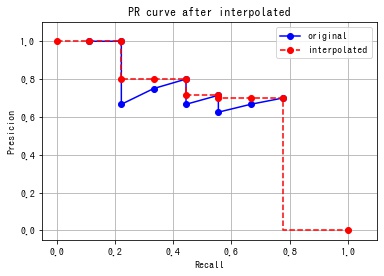
Recall が $r_1, r_2, \cdots, r_N$、Precision が $P(r_1), P(r_2), \cdots, P(r_N)$ としたとき、補完後の PR 曲線の下側の面積を以下のように求めます。
$$ \mathrm{AP} = \sum_{i = 2}^N (r_i – r_{i – 1}) P(r_i) $$numpy.diff() で各短冊の幅 $r_i – r_{i – 1}$ を求めて、短冊の高さ $P(r_i)$ と乗算したのち、numpy.ndarray.sum() で総和をとることで、短冊の面積の合計 (下の赤い領域) を計算します。
# AP を計算する。
average_precision = (np.diff(modified_recall) * modified_precision[1:]).sum()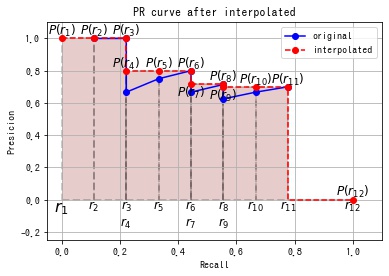
mAP
クラスごとに算出した AP の平均をとったものが mean Average Precision (mAP) となります。
クラス数が $C$ で、クラス $i$ の AP が $\mathrm{AP}_i$ としたとき、mAP は次のように計算されます。
$$ \mathrm{mAP} = \frac{1}{C} \sum_{i = 1}^C \mathrm{AP}_i $$例:
| クラス | AP |
|---|---|
| 人 | 0.98 |
| 犬 | 0.78 |
| 猫 | 0.83 |
| mAP | 0.86 |
実装例
GitHub に mAP の計算を行う実装例をおきました。 使い方は、README を見てください。
参考文献
- GitHub – rafaelpadilla/Object-Detection-Metrics: Most popular metrics used to evaluate object detection algorithms.
Pascal VOC の mAP 計算方法の説明及び実装例があります。


コメント
コメント一覧 (0件)
物体検出における TP、FP、FNの節の正解かどうかの表,1列目はc,d,eの順ではなくd,c,eでしょうか?
To: yumion さん
d が正解、c, f は不正解になり、記載の表が間違っていたので、修正しました。
コメントしていただきありがとうございます。