概要
情報理論について解説します。
自己情報量
確率質量関数 $p_X(x)$ を持つ離散確率変数 $X$ について、観測値 $x$ が抽出されたときに得られる情報の量を情報量 (infomation content)、自己情報量 (self-infomation) または驚き (surprisal) といい、次で定義します。
$$ I_X(x) \coloneqq -\log p_X(x) = \log \frac{1}{p_X(x)} $$対数関数 $\log$ の底はなんでもよいですが、底の値によって、次の単位を用います。
- $2$: ビット (bit) またはシャノン (shannon)
- $e$: ナット (nat)
- $10$: デシット (decit) またはハートレー (hartley)
例: 偏りがないコイン投げ
表が出たとき $1$、裏が出たとき $0$ をとる確率変数を $X$ とします。 偏りがないコインなので、
$$ p_X(x) = 0.5, (x = 0, 1) $$このとき、表がでたとわかったときに得られる情報量は
$$ I_X(0) = -\log_2 p_X(0) = -\log_2 \frac{1}{2} = 1 bit $$裏がでたとわかったときに得られる情報量は
$$ I_X(1) = -\log_2 p_X(1) = -\log_2 \frac{1}{2} = 1 bit $$例: 偏りがないサイコロ投げ
サイコロの出た目をとる確率変数を $X$ とします。 偏りがないサイコロなので、
$$ p_X(x) = 0.5, (x = 1, 2, 3, 4, 5, 6) $$このとき、$4$ がでたとわかったときに得られる情報量は
$$ I_X(0) = -\log_2 p_X(4) = -\log_2 \frac{1}{6} \approx 2.585 bit $$import matplotlib.pyplot as plt
import numpy as np
with np.errstate(divide='ignore'):
p = np.linspace(0, 1)
y = -np.log2(p)
fig, ax = plt.subplots()
ax.plot(p, y, label=r"$-\log_2 x$")
ax.legend()
ax.grid()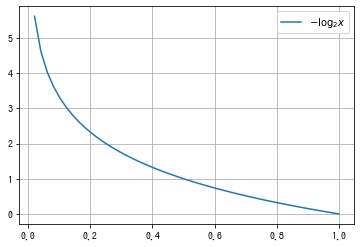
起こりにくい事象ほど、それが起こったときに得られる情報量は大きいと解釈できます。また自己情報量は $0$ より大きい値になります。
平均情報量、エントロピー
確率質量関数 $p_X(x)$ を持つ離散確率変数 $X$ について、$X$ のシャノンのエントロピー (Shannon entropy) または平均情報量 (average infomation) を次で定義します。
$$ \begin{aligned} H(X) &\coloneqq E[I_X(X)] \\ &= \sum_x p_X(x) I_X(x) \\ &= \sum_x -p_X(x) \log p_X(x) \\ \end{aligned} $$例: くじ引き
アタリが出たとき $1$、ハズレが出たとき $0$ をとる確率変数を $X$ とします。 アタリの確率を $p$ とすると、ハズレの確率は $1 – p$ とします。
$$ p_X(x) = \begin{cases} p & x = 1 \\ 1 – p & x = 0 \end{cases} $$このとき、$X$ の平均情報量は、
$$ \begin{aligned} H(X) &= -p_X(1) \log p_X(1) -p_X(0) \log p_X(0) \\ &= -p \log p -(1 – p) \log (1 – p) \end{aligned} $$$p$ の値を変えたときに平均情報量 $H(X)$ がどのように変化するかをグラフにします。
import matplotlib.pyplot as plt
import numpy as np
# 各 p における平均情報量
with np.errstate(divide="ignore", invalid='ignore'):
p = np.linspace(0, 1, 100)
H = -p * np.log(p) - (1 - p) * np.log(1 - p)
# 描画する。
fig, ax = plt.subplots(facecolor="w")
ax.set_xlabel("$p$")
ax.set_xticks(np.linspace(0, 1, 11))
ax.set_ylabel("$H(X)$")
ax.grid()
ax.plot(p, H)
plt.show()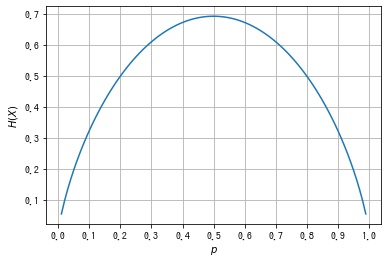
平均情報量は $p = 0$ (アタリなし) と $p = 1$ (ハズレなし) のときに最小、$p = 0.5$ (アタリ、ハズレが同じ確率) のとき最大となることがわかります。
情報量の性質
加法性 (additivity)
独立な離散確率変数 $X, Y$ がそれぞれ確率質量関数 $p_X(x), p_Y(y)$ を持つとき、結合確率密度関数は
$$ p_{X, Y}(x, y) = P(X = x, Y=y) = p_X(x) p_Y(y) $$となります。このとき、$(X, Y) = (x, y)$ となる自己情報量は
$$ \begin{aligned} I_{X, Y}(x, y) &= -\log p_{X, Y}(x, y) \\ &= -\log p_X(x) p_Y(y) \\ &= -\log p_X(x) -\log p_Y(y) \\ &= I_X(x) + I_Y(y) \\ \end{aligned} $$情報量は減少関数である
確率質量関数 $p_X(x)$ を持つ離散確率変数 $X$ について、自己情報量 $I_X(x)$ は確率 $p_X(x)$ に関する減少関数となっています。
平均情報量の最小値、最大値
シャノンの補助定理
$X, Y$ をそれぞれ $n$ 個の値をとり得る離散確率変数とし、各値をとる確率はそれぞれ $p_i, q_i, (i = 1, 2, \cdots, n)$ とします。 このとき、次が成り立ちます。
$$ -\sum_{i = 1}^n p_i \log_a p_i \le -\sum_{i = 1}^n p_i \log_a q_i $$証明)
$$ \begin{aligned} & -\sum_{i = 1}^n p_i \log_a q_i + \sum_{i = 1}^n p_i \log_a p_i \\ &= -\sum_{i = 1}^n p_i (\log_a q_i – \log_a p_i) \\ &= -\sum_{i = 1}^n p_i \log_a \frac{q_i}{p_i} \\ &= \sum_{i = 1}^n \frac{p_i}{\log a} \left( -\log \frac{q_i}{p_i} \right) \quad \because 底の変換公式\ (a \to e) \\ \end{aligned} $$ここで、不等式 $\log x \le x – 1 \Leftrightarrow 1 – x \le -\log x$ を用いると、
$$ \begin{aligned} \sum_{i = 1}^n \frac{p_i}{\log a} \left( -\log \frac{q_i}{p_i} \right) &\ge \sum_{i = 1}^n \frac{p_i}{\log a} \left( 1 – \frac{q_i}{p_i} \right) \\ &= \frac{1}{\log a} \sum_{i = 1}^n (p_i – q_i) \\ &= \frac{1}{\log a} \left(\sum_{i = 1}^n p_i – \sum_{i = 1}^n q_i \right) \\ &= 0 \quad \because \sum_{i = 1}^n p_i = 1, \sum_{i = 1}^n q_i = 1 \end{aligned} $$よって、
$$ -\sum_{i = 1}^n p_i \log p_i \le -\sum_{i = 1}^n p_i \log q_i $$下限
$X$ を確率質量関数 $p_X(x)$ を持つ離散確率変数とします。 確率関数なので $p_X(x) \ge 0, -\log p_X(x) \ge 0$ より、
$$ H(X) = \sum_x -p_X(x) \log p_X(x) \ge 0 $$等号は $p_X(x)$ がある値 $a$ で $1$、それ以外で $0$ をとる確率質量関数であるとします。
$$ p_X(x) = \begin{cases} 1 & X = a \\ 0 & otherwise \end{cases} $$つまり、$X = a$ となる確率が $1$ の場合に平均情報量は最小値 $0$ をとります。
上限
$X$ を $n$ 個の値をとり得る離散確率変数とし、各値をとる確率は $p_i, (i = 1, 2, \cdots, n)$ とします。 $Y$ を $n$ 個の値をとり得る離散確率変数とし、各値をとる確率は $q_i = \frac{1}{n}, (i = 1, 2, \cdots, n)$ とします (離散一様分布)。
このとき、
$$ \begin{aligned} H(X) &= -\sum_{i = 1}^n p_i \log p_i \\ &\le -\sum_{i = 1}^n p_i \log q_i \\ &= -\sum_{i = 1}^n p_i \log \frac{1}{N} \\ &= \sum_{i = 1}^n p_i \log N \\ &= \log N \quad \because \sum_{i = 1}^n p_i = 1 \end{aligned} $$

コメント