機械学習 – 最大事後確率 (MAP) 識別規則
概要
識別規則の1つである最大事後確率規則について解説します。
Advertisement
最大事後確率規則 (MAP decision rule)
事後確率 $p(c_i|\bm{x})$ が最大となるクラスに割り当てる識別規則を最大事後確率識別規則 (maximum a posterior classifier ecision rule/MAP ecision rule) といいます。
- 識別関数
- 決定境界
クラス $c_i$ の決定領域は
$$ \begin{aligned} \mathcal{R}_i &= \{ \bm{x} \in \R^d | c_i = \argmax_j p(c_j | \bm{x}) \} \end{aligned} $$- 識別クラス
入力 $\bm{x}$ の識別クラス $\hat{y}$ は
$$ \begin{aligned} \hat{y} &= \argmax_i p(c_i|\bm{x}) \\ &= c_i \ \text{s.t.} \ p(c_i|\bm{x}) \ge p(c_j|\bm{x}), (i \ne j) \end{aligned} $$ベイズの定理 $p(c_i|\bm{x}) = \frac{p(\bm{x}|c_i) p(c_i)}{p(\bm{x})}$ を適用すると、以下のように書き換えられます。
$$ \begin{aligned} \hat{y} &= \argmax_i \frac{p(\bm{x}|c_i) p(c_i)}{p(\bm{x})} \\ &= \argmax_i p(\bm{x}|c_i) p(c_i) \quad \because p(\bm{x}) はすべての i で共通\\ &= c_i \ \text{s.t.} \ p(\bm{x}|c_i) p(c_i) \ge p(\bm{x}|c_j) p(c_j), (i \ne j) \\ \end{aligned} $$- 誤り率
最大事後確率識別規則の誤り率を
$$ \varepsilon(\bm{x}) = E[1 – \max_i p(c_i|\bm{x})] $$と定義すると、その期待値は
$$ \begin{aligned} E[\varepsilon(\bm{x})] &= E[1 – \max_j p(c_j|\bm{x})] \\ &= 1 – E[\max_j p(c_j|\bm{x})] \\ &= 1 – \int_{\R^d} \max_j p(c_j|\bm{x}) p(\bm{x}) d\bm{x} \quad \because 期待値の定義 \\ &= 1 – \sum_{i = 1}^K \int_{\mathcal{R}_i} \max_j p(c_j|\bm{x}) p(\bm{x}) d\bm{x} \quad \because \mathcal{R}_1, \mathcal{R}_2, \cdots, \mathcal{R}_K は \R^d の分割 \\ &= 1 – \sum_{i = 1}^K \int_{\mathcal{R}_i} p(c_i|\bm{x}) p(\bm{x}) d\bm{x} \quad \because \bm{x} \in \mathcal{R}_i \to p(c_i|\bm{x}) = \max_j p(c_j|\bm{x}) p(c_j) \\ &= 1 – \sum_{i = 1}^K \int_{\mathcal{R}_i} p(\bm{x}|c_i) p(c_i) d\bm{x} \quad \because ベイズの定理 \\ \end{aligned} $$例: 2クラス分類
釣った魚の大きさが $x \in \R$ であったとき、その魚が鮭 (salmon)、スズキ (sea bass) のどちらであるかを識別する2クラス分類問題を考えます。(鮭、スズキ以外の魚が釣れることはないと仮定します)
以下の情報がわかっているものとします。
- 事前確率
- 釣った魚が鮭である確率は $p(salmon) = \frac{2}{3}$
- 釣った魚がスズキである確率は $p(bass) = \frac{1}{3}$
- 尤度
- 鮭の大きさは正規分布 $\mathcal{N}(5, 1)$ に従う $$ p(x|salmon) = \frac{1}{\sqrt{2 \pi}} \exp \left( -\frac{(x – 5)^2}{2} \right) $$
- スズキの大きさは正規分布 $\mathcal{N}(10, 4)$ に従う $$ p(x|bass) = \frac{1}{2 \sqrt{2 \pi}} \exp \left( -\frac{(x – 10)^2}{8} \right) $$
ベイズの定理より、事後確率は
$$ \begin{aligned} p(salmon|x) &= \frac{1}{\sqrt{2 \pi}} \exp \left( -\frac{(x – 5)^2}{2} \right) \times \frac{2}{3} \\ p(bass|x) &= \frac{1}{2 \sqrt{2 \pi}} \exp \left( -\frac{(x – 10)^2}{8} \right) \times \frac{1}{3} \\ \end{aligned} $$このとき、最大事後確率識別規則に従うと、予測クラスは
$$ \begin{aligned} \hat{y} &= \begin{cases} salmon & \text{if} \ p(salmon|x) \ge p(bass|x) \\ bass & \text{if} \ p(salmon|x) < p(bass|x) \end{cases} \\ \end{aligned} $$$p(x|salmon), p(x|bass)$ 及び $p(salmon|x), p(bass|x)$ を描画すると以下のようになります。
In [1]:
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm
x = np.linspace(0, 20, 100)
salmon_y1 = norm.pdf(x, loc=5, scale=1)
bass_y1 = norm.pdf(x, loc=10, scale=2)
salmon_y2 = norm.pdf(x, loc=5, scale=1) * 2 / 3
bass_y2 = norm.pdf(x, loc=10, scale=2) * 1 / 3
error = 1 - np.maximum(salmon_y2, bass_y2)
fig, ax = plt.subplots(figsize=(9, 6))
ax.plot(x, salmon_y1, "b", alpha=0.5, label=r"$p(x|salmon)$")
ax.plot(x, bass_y1, "g", alpha=0.5, label=r"$p(x|bass)$")
ax.plot(x, salmon_y2, "b", label=r"$p(salmon|x)$")
ax.plot(x, bass_y2, "g", label=r"$p(bass|x)$")
ax.plot(x, error, "r", label=r"$\varepsilon(x)$")
ax.set_xlabel("Length")
ax.grid()
ax.legend()
plt.show()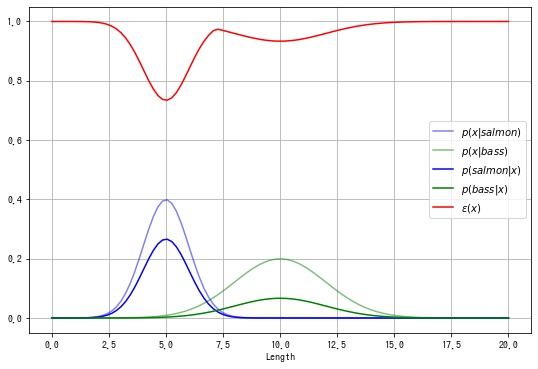
このとき、鮭とスズキの決定領域は以下になります。
$$ \begin{aligned} \mathcal{R}_{salmon} &= \{\bm{x} \in \R^d| p(salmon|x) \ge p(bass|x) \} \\ \mathcal{R}_{bass} &= \{\bm{x} \in \R^d| p(salmon|x) < p(bass|x) \} \end{aligned} $$Sympy で $p(salmon|x) = p(bass|x)$ を解いて、最尤識別規則の決定境界を計算します
In [2]:
import sympy as sym
from sympy.stats import density, Normal
x = sym.symbols("x")
salmon_pdf = density(Normal("salmon", 5, 1))(x) * 2 / 3
bass_pdf = density(Normal("bass", 10, 2))(x) * 1 / 3
# 方程式を解く。
ret = sym.solve(salmon_pdf - bass_pdf)
# 数値解にする。
x1, x2 = sym.N(ret[0]), sym.N(ret[1])
print(x1, x2)-0.514769585521292 7.18143625218796
$p(salmon|x) = p(bass|x)$ の解は $x = -0.51, 7.18$ であるとわかります。 鮭が釣れる確率が高いという事前確率が得られたことにより、決定境界が右に移動しました。
-
前の記事
機械学習 – 最尤識別規則 2020.07.10
-
次の記事
機械学習 – 棄却オプション 2020.07.10