機械学習 – 最尤識別規則

概要

識別規則の1つである最尤識別規則について解説します。

最尤識別規則 (ML decision rule)

尤度 $p(\bm{x}|c_i)$ が最大となるクラスに割り当てる識別規則を最尤識別規則 (maximum likelihood decision rule/ML decision rule) といいます。

識別関数

$$ g_i(\bm{x}) = p(\bm{x}|c_i), (i = 1, 2, \cdots, K) $$

決定境界

クラス $c_i$ の決定領域は

$$ \mathcal{R}_i = \{\bm{x} \in \R^d| c_i = \argmax_j p(\bm{x}|c_j)\} $$

識別クラス

入力 $\bm{x}$ の識別クラス $\hat{y}$ は

$$ \begin{aligned} \hat{y} &= \argmax_i p(\bm{x}|c_i) \\ &= c_i \ \text{s.t.} \ p(\bm{x}|c_i) \ge p(\bm{x}|c_j), (i \ne j) \end{aligned} $$

誤り率

最尤識別規則の誤り率を

$$ \varepsilon(\bm{x}) = E[1 – \max_i p(\bm{x}|c_i)] $$

と定義すると、その期待値は

$$ \begin{aligned} E[\varepsilon(\bm{x})] &= E[1 – \max_j p(\bm{x}|c_j)] \\ &= 1 – E[\max_j p(\bm{x}|c_j)] \\ &= 1 – \int_{\R^d} \max_j p(\bm{x}|c_j) p(\bm{x}) d\bm{x} \quad \because 期待値の定義 \\ &= 1 – \sum_{i = 1}^K \int_{\mathcal{R}_i} \max_j p(\bm{x}|c_j) p(\bm{x}) d\bm{x} \quad \because \mathcal{R}_1, \mathcal{R}_2, \cdots, \mathcal{R}_K は \R^d の分割 \\ &= 1 – \sum_{i = 1}^K \int_{\mathcal{R}_i} p(\bm{x}|c_i) p(\bm{x}) d\bm{x} \quad \because \bm{x} \in \mathcal{R}_i \to p(\bm{x}|c_i) = \max_j p(\bm{x}|c_j) \\ \end{aligned} $$

例: 2クラス分類

釣った魚の大きさが $x \in \R$ であったとき、その魚が鮭 (salmon)、スズキ (sea bass) のどちらであるかを識別する2クラス分類問題を考えます。(鮭、スズキ以外の魚が釣れることはないと仮定します)

以下の情報がわかっているものとします。

鮭の大きさは正規分布 $\mathcal{N}(5, 1)$ に従う $$ p(x|salmon) = \frac{1}{\sqrt{2 \pi}} \exp \left( -\frac{(x – 5)^2}{2} \right) $$
スズキの大きさは正規分布 $\mathcal{N}(10, 4)$ に従う $$ p(x|bass) = \frac{1}{2 \sqrt{2 \pi}} \exp \left( -\frac{(x – 10)^2}{8} \right) $$

このとき、最尤識別規則に従うと、予測クラスは

$$ \begin{aligned} \hat{y} &= \begin{cases} salmon & \text{if} \ p(x|salmon) \ge p(x|bass) \\ bass & \text{if} \ p(x|salmon) < p(x|bass) \end{cases} \\ \end{aligned} $$

$p(x|salmon), p(x|bass)$ を描画すると以下のようになります。

In [1]:

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm

x = np.linspace(0, 20, 100)

salmon_y = norm.pdf(x, loc=5, scale=1)
bass_y = norm.pdf(x, loc=10, scale=2)
error = 1 - np.maximum(salmon_y, bass_y)

fig, ax = plt.subplots(figsize=(9, 6))
ax.plot(x, salmon_y, "b", label=r"$p(x|salmon)$")
ax.plot(x, bass_y, "g", label=r"$p(x|bass)$")
ax.plot(x, error, "r", label=r"$\varepsilon(x)$")

ax.set_xlabel("Length")
ax.grid()
ax.legend()

plt.show()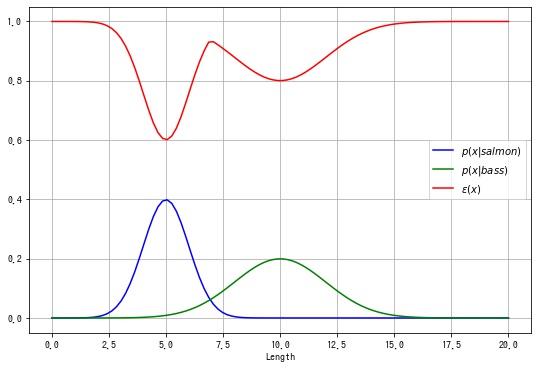

このとき、鮭とスズキの決定領域は以下になります。

$$ \begin{aligned} \mathcal{R}_{salmon} &= \{\bm{x} \in \R^d| p(x|salmon) \ge p(x|bass) \} \\ \mathcal{R}_{bass} &= \{\bm{x} \in \R^d| p(x|salmon) < p(x|bass) \} \end{aligned} $$

Sympy で $p(x|salmon) = p(x|bass)$ を解いて、最尤識別規則の決定境界を計算します

In [2]:

import sympy as sym
from sympy.stats import density, Normal

x = sym.symbols("x")

salmon_pdf = density(Normal("salmon", 5, 1))(x)
bass_pdf = density(Normal("bass", 10, 2))(x)

# 方程式を解く。
ret = sym.solve(salmon_pdf - bass_pdf)

# 数値解にする。
x1, x2 = sym.N(ret[0]), sym.N(ret[1])
print(x1, x2)