概要
物体検出で用いられる Non Maximum Suppression の仕組み及び実装について紹介します。
Non Maximum Suppression
物体検出を行うと、1つの物体に対して複数回検出されるということがあります。 そのため、物体検出では重複した検出結果を1つに統合する Non Maximum Suppression という後処理がよく用いられます。
矩形の表現
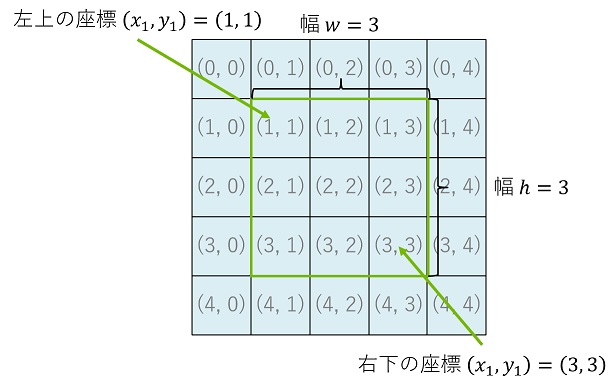
短形の左上の座標を $(x_1, y_1)$、右下の座標を $(x_2, y_2)$、幅及び高さを $(w, h)$ とします。
$(x_1, y_1), (x_2, y_2)$ から $(w, h)$ を求めるには、$w = x_2 – x_1 + 1, h = y_2 – y_1 + 1$、 逆に $(x_1, y_1), (w, h)$ から $(x_2, y_2)$ を求めるには、$x_2 = x_1 + w – 1, y_2 = y_1 + h – 1$ となることに注意してください。
Overlap Ratio
2つの矩形 $a, b$ があったとき、$\frac{area(a \cap b)}{area(a)}$ で計算できる値を Overlap Ratio といいます。 2つの矩形が完全に一致していれば $OverlapRatio = 1$、全く重なっていなかったら $OverlapRatio = 0$ をとります。
Non Maximum Suppression の処理
入力として、スコア付きの矩形が渡され、以下のアルゴリズムで動作します。
- 入力からスコアが一番高い矩形を選択し、出力に移す
- 選択した矩形と入力に残っている各矩形の IOU を計算し、閾値以上のものを入力から削除する (選択した矩形とある程度重なっている矩形は同じ物体であると判断する。)
- 入力が空になるまで1、2を繰り返す
- 入力が空になったら、出力にある矩形を結果出力とする
閾値の設定
重複と判断して削除する Overlap Ratio の閾値を $[0, 1]$ の範囲で適切な値に決める必要があります。値が大きいほど重複と判断する基準が厳しくなり、同一物体に複数の矩形が残ってしまう可能性があります。逆に、値が低いほど重複と判断する基準が緩くなり、異なる物体を示している矩形が同じ物体を示していると判断され、削除される可能性があります。
実装
例として、テンプレートマッチングの重複した検出結果を Non Maximum Suppression の入力として使用します。
入力画像
テンプレート画像
テンプレートマッチングを行う
テンプレートマッチングを行い、類似度が 0.9 以上の短形を検出されたと判定します。
import cv2
import numpy as np
from IPython.display import Image, display
from matplotlib import pyplot as plt
def imshow(img):
"""ndarray 配列をインラインで Notebook 上に表示する。
"""
ret, encoded = cv2.imencode(".jpg", img)
display(Image(encoded))
# 入力画像、テンプレート画像を読み込む。
img = cv2.imread("sample.jpg") # 入力画像
templ = cv2.imread("template.jpg") # テンプレート画像
# テンプレートマッチングを行う。
result = cv2.matchTemplate(img, templ, cv2.TM_CCOEFF_NORMED)
# 類似度が 0.6 以上の位置及びスコアを取得する。
positions = np.where(result >= 0.9)
scores = result[positions]
# 各要素が (x1, y1, x2, y2) である短形一覧を作成する。
boxes = []
h, w = templ.shape[:2] # テンプレート画像の高さ及び幅
for y, x in zip(*positions):
boxes.append([x, y, x + w - 1, y + h - 1])
boxes = np.array(boxes)検出結果を描画する
この時点で検出結果を描画すると、以下のようになります。 1つの物体として検出されているように見えますが、実際は複数の矩形が重なってします。
def draw_boxes(img, boxes):
dst = img.copy()
for x1, y1, x2, y2 in boxes:
cv2.rectangle(
dst, (x1, y1), (x2, y2), color=(0, 255, 0), thickness=2,
)
imshow(dst)
print("number of boxes", len(boxes))
# 描画する。
draw_boxes(img, boxes)
number of boxes 16
Non Maximum Suppression を実装する
def non_max_suppression(boxes, scores, overlap_thresh):
"""Non Maximum Suppression (NMS) を行う。
Args:
boxes: (N, 4) の numpy 配列。矩形の一覧。
overlap_thresh: [0, 1] の実数。閾値。
Returns:
boxes : (M, 4) の numpy 配列。Non Maximum Suppression により残った矩形の一覧。
"""
if len(boxes) <= 1:
return boxes
# float 型に変換する。
boxes = boxes.astype("float")
# (NumBoxes, 4) の numpy 配列を x1, y1, x2, y2 の一覧を表す4つの (NumBoxes, 1) の numpy 配列に分割する。
x1, y1, x2, y2 = np.squeeze(np.split(boxes, 4, axis=1))
# 矩形の面積を計算する。
area = (x2 - x1 + 1) * (y2 - y1 + 1)
indices = np.argsort(scores) # スコアを降順にソートしたインデックス一覧
selected = [] # NMS により選択されたインデックス一覧
# indices がなくなるまでループする。
while len(indices) > 0:
# indices は降順にソートされているので、一番最後の要素の値 (インデックス) が
# 残っている中で最もスコアが高い。
last = len(indices) - 1
selected_index = indices[last]
remaining_indices = indices[:last]
selected.append(selected_index)
# 選択した短形と残りの短形の共通部分の x1, y1, x2, y2 を計算する。
i_x1 = np.maximum(x1[selected_index], x1[remaining_indices])
i_y1 = np.maximum(y1[selected_index], y1[remaining_indices])
i_x2 = np.minimum(x2[selected_index], x2[remaining_indices])
i_y2 = np.minimum(y2[selected_index], y2[remaining_indices])
# 選択した短形と残りの短形の共通部分の幅及び高さを計算する。
# 共通部分がない場合は、幅や高さは負の値になるので、その場合、幅や高さは 0 とする。
i_w = np.maximum(0, i_x2 - i_x1 + 1)
i_h = np.maximum(0, i_y2 - i_y1 + 1)
# 選択した短形と残りの短形の Overlap Ratio を計算する。
overlap = (i_w * i_h) / area[remaining_indices]
# 選択した短形及び OVerlap Ratio が閾値以上の短形を indices から削除する。
indices = np.delete(
indices, np.concatenate(([last], np.where(overlap > overlap_thresh)[0]))
)
# 選択された短形の一覧を返す。
return boxes[selected].astype("int")Non Maximum Suppression を適用する。
Non Maximum Suppression を適用します。その結果、複数あった検出結果が1個に統合されているのが確認できます。
# Non Maximum Suppression を行う。
boxes = non_max_suppression(boxes, scores, overlap_thresh=0.6)
# NMS 後に残った短形一覧を描画する。
draw_boxes(img, boxes)
number of boxes 1












コメント
コメント一覧 (0件)
①「テンプレートマッチングを行う」を実行してから、②「検出結果を描画する」の最後に
cv2.imwrite(’ファイル名’ , dst) と追記して実行しますと、sample画像に16ヶの矩形が表示
された画像が保存されました。
その後に、
③「Non Maximum Suppression を実装する」 def non_max_suppression・・・・
④「Non Maximum Suppression を適用する」 boxes = non_ max_・・・・
をそのまま追記し、cv2.imwrite()~の()内を①②実行時と同名のファイル名でその表記位置
のままにして、③④を実行しましすと、sample画像に1ヶの矩形が表示されました。
②の直後に記したcv2.imwrite()~はそのままの位置なのに、何故その結果が変わるのか
が解らないのですが、3つ目のdef分(def non_max_suppression・・・)以下最後までのコードは、
2つ目のdef分(def draw_boxes・・・)よりも前に実行されるのでしょうか?
コメントありがとうございます。本ブログのコード部分はコードの上の In [番号] を上から順番に実行していくことを想定しております。
本記事の場合、上から ln[1]、ln[2]、ln[3]、ln[4] の順番で実行します。
> cv2.imwrite()~はそのままの位置なのに、何故その結果が変わるのか
が解らないのですが、
Jupyter Notebook で実行していますでしょうか。その場合、前の実行結果がそのまま残るので、セルの位置が変わらなくても2回目は実行結果が変わる可能性があります。
セルを上から順番に実行すると、ブログと同じ結果になると思います。
—-
矩形を1つにしたあとの結果を画像に保存したい場合は、以下のようにしてみてください。
boxes = non_max_suppression(boxes, scores, overlap_thresh=0.6) dst = img.copy() for x1, y1, x2, y2 in boxes: cv2.rectangle(dst, (x1, y1), (x2, y2), color=(0, 255, 0), thickness=2) cv2.imwrite("result.png", dst)