目次
概要
OpenCV の特徴点マッチングを利用して物体を検出する方法について解説します。
物体検出の手順
画像を読み込む
入力画像 1 の物体を入力画像 2 から探します。
入力画像 1
入力画像 2
物体ごとにマスクを作成する
特徴量マッチングは 1 対 1 の物体同士で行うものですが、2 枚目の画像には複数の物体が写っているため、これを 1 つずつ比較できるように物体ごとのマスクを作成します。
In [1]:
import cv2
from IPython.display import Image, display
def imshow(img):
"""ndarray 配列をインラインで Notebook 上に表示する。"""
ret, encoded = cv2.imencode(".jpg", img)
display(Image(encoded))
In [2]:
import cv2
import numpy as np
def get_contours(img):
# HSV 色空間に変換する。
hsv = cv2.cvtColor(img, cv2.COLOR_BGR2HSV)
# 2値化する。
bin_img = cv2.inRange(hsv, (0, 0, 0), (255, 200, 255))
# 輪郭を滑らかにする。
bin_img = cv2.medianBlur(bin_img, 5)
imshow(bin_img)
# 輪郭を抽出する。
contours, hierarchy = cv2.findContours(
bin_img, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE
)
# 面積が小さい輪郭は除去する。
contours = list(filter(lambda x: cv2.contourArea(x) > 100, contours))
# 輪郭抽出の結果を描画する。
dst = cv2.drawContours(img.copy(), contours, -1, color=(0, 0, 255), thickness=2)
imshow(dst)
return contours
# 画像を読み込む。
train_img = cv2.imread("sample1.jpg") # 探したい物体
query_img = cv2.imread("sample2.jpg")
# 輪郭を抽出する。
train_contours = get_contours(train_img)
query_contours = get_contours(query_img)
# 検出結果を格納するオブジェクト
train_obj = {"contour": train_contours[0]}
query_objs = [{"contour": x} for x in query_contours]
# 各物体のマスクを作成する。
for obj in query_objs:
# 輪郭内部を255、それ以外を0としたマスク画像を作成する。
mask = np.zeros(train_img.shape[:2], dtype=np.uint8)
cv2.drawContours(mask, [obj["contour"]], -1, color=255, thickness=-1)
imshow(mask)
obj["mask"] = mask

特徴点および特徴量記述子を計算する
探したい物体および検出対象の画像に写っている物体の特徴点および特徴量記述子を計算します。
In [3]:
# OBR 特徴量検出器を作成する。
detector = cv2.ORB_create()
# 探したい物体の特徴点及び特徴量記述子を計算する。
train_kp, train_desc = detector.detectAndCompute(train_img, None)
# 検出対象の画像の物体の特徴点及び特徴量記述子を計算する。
for obj in query_objs:
obj["kp"], obj["desc"] = detector.detectAndCompute(query_img, obj["mask"])特徴点マッチングを行う
探したい物体の特徴量と検出対象の画像に写っている物体の特徴量をそれぞれマッチングし、良好なマッチング結果が得られたものをマッチしたと判定します。
bf.knnMatch()で kNN 法を用いてマッチングを行う- レシオテストを行い、信頼度の低いマッチング結果を除外する
- マッチした特徴点の数が閾値以上かどうかで、その輪郭が探したい物体かどうかを判定する
In [4]:
# マッチング器を作成する。
bf = cv2.BFMatcher(cv2.NORM_HAMMING)
for obj in query_objs:
# 特徴点マッチングを行う。
matches = bf.knnMatch(obj["desc"], train_desc, k=2)
# レシオテストを行う。
good_matches = []
for first, second in matches:
if first.distance < second.distance * 0.7:
good_matches.append(first)
# マッチング結果を描画する。
dst = cv2.drawMatches(query_img, obj["kp"], train_img, train_kp, good_matches, None)
imshow(dst)
if len(good_matches) > 100:
# 十分な数のマッチングが存在する場合、同一物体と判定する。
obj["is_target"] = True
# マッチした特徴点を格納する。
obj["match_query_kp"] = np.array(
[obj["kp"][x.queryIdx].pt for x in good_matches]
)
obj["match_train_kp"] = np.array(
[train_kp[x.trainIdx].pt for x in good_matches]
)
else:
obj["is_target"] = False
# 検出できた物体だけ残す
query_objs = [x for x in query_objs if x["is_target"]]


検出した物体の矩形を計算する
検出した物体の輪郭の外接矩形及び重心を計算します。
In [5]:
def get_rect(contour):
# 輪郭の外接矩形を取得する。
x, y, w, h = cv2.boundingRect(contour)
# 輪郭のモーメントを計算する。
M = cv2.moments(contour)
# モーメントから重心を計算する。
cx = M["m10"] / M["m00"]
cy = M["m01"] / M["m00"]
return {"tl": (x, y), "br": (x + w, y + h), "center": (cx, cy)}
def to_int_tuple(pt):
return tuple(int(x) for x in pt)
train_obj.update(get_rect(train_obj["contour"]))
for obj in query_objs:
obj.update(get_rect(obj["contour"]))
# 外接矩形及び重心を描画する。
dst = query_img.copy()
for obj in query_objs:
# 矩形を描画する。
cv2.rectangle(dst, obj["tl"], obj["br"], color=(0, 0, 255), thickness=2)
# 中心を描画する。
cv2.circle(dst, to_int_tuple(obj["center"]), 5, color=(0, 0, 255), thickness=-1)
imshow(dst)
検出した物体の姿勢推定を行う
2 つの同じ大きさの画像に同じ対象物が写っており、それらが平面上を回転及び平行移動した結果であるとわかっている場合、先程求めた特徴点の対応関係よりアフィン変換行列を推定し、回転角度や平行移動量を算出することができます。
In [6]:
from matplotlib import pyplot as plt
for obj in query_objs:
# ホモグラフィー行列を求める。
query_kp = np.expand_dims(obj["match_query_kp"], axis=1)
train_kp = np.expand_dims(obj["match_train_kp"], axis=1)
H, inliers = cv2.estimateAffinePartial2D(train_kp, query_kp)
h, w = train_img.shape[:2]
fig, ax = plt.subplots()
ax.scatter(train_kp[:, 0, 0], train_kp[:, 0, 1], s=20, c="b", label="train")
ax.scatter(query_kp[:, 0, 0], query_kp[:, 0, 1], s=20, c="r", label="query")
ax.set_xlim(0, w)
ax.set_ylim(0, h)
ax.grid()
ax.legend()
plt.show()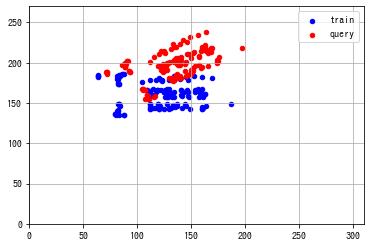
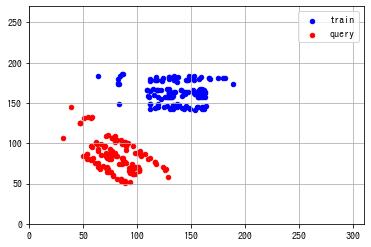
In [7]:
def calc_pose(query_kp, train_kp):
query_kp = np.reshape(query_kp, (-1, 1, 2))
train_kp = np.reshape(train_kp, (-1, 1, 2))
# ホモグラフィー行列を求める。
A, inliers = cv2.estimateAffinePartial2D(train_kp, query_kp)
# 行列から平行移動量を求める。
M = A[:2, :2]
t = A[:, 2]
# 行列から回転角度を求める。
degree = np.rad2deg(-np.arctan2(A[0, 1], A[0, 0]))
return {"angle": degree, "M": M, "t": t}
for obj in query_objs:
obj.update(calc_pose(obj["match_query_kp"], obj["match_train_kp"]))
In [8]:
# 平行移動及び回転角度を描画する。
img = cv2.addWeighted(train_img, 0.5, query_img, 0.5, 0)
for obj in query_objs:
src = np.array(train_obj["center"])
# 移動前の点に推定したアフィン変換 M x + b を適用する。
dst = obj["M"] @ src + obj["t"]
# アフィン変換後の点及び回転量を描画して、合っていることを確かめる。
# アフィン変換後の点を描画する。
cv2.arrowedLine(
img, to_int_tuple(src), to_int_tuple(dst), color=(0, 0, 255), thickness=2
)
# 回転量を描画する。
cv2.ellipse(
img,
to_int_tuple(dst),
(20, 20),
angle=0,
startAngle=0,
endAngle=obj["angle"],
color=(0, 0, 0),
thickness=-1,
)
imshow(img)
推定したアフィン変換行列が概ね正しいことが確認できます。












コメント
コメント一覧 (0件)
こんにちは。
すばらしい投稿誠にありがとうございます。
Google Colaboratory で試してみました。
import matplotlib.pyplot as pltを追加し、plt.imshow(dst) と表記することで
無事表示できました。
※Google Colaboratoryですと、全部の画像が表示できず、最後の画像しか表示できないため、
改善方法を模索中です。
サンプル画像では無事に表示できたのですが、次に試しに、背景を黒色とした金属部品で
試したのですが、うまくいきませんでした。
画像のサイズは250X200です。
すみません、よろしければ、うまくいく方法をご教示頂くことできませんでしょうか?
コメントありがとうございます。
> Google Colaboratoryですと、全部の画像が表示できず、最後の画像しか表示できないため、改善方法を模索中です。
記事内の imshow() は In [1] のコード内で定義している imshow() 関数を呼び出すことを想定しています。Google Colab の IPython のバージョンが古いので、 !pip3 install –upgrade IPython
をセルに入力して IPython をアップデート後にカーネルを再起動すれば、記事のコードでも画像が表示されると思います。
また、代わりに matplotlib の plt.imshow() を使う場合は、plt.show() をその直後に呼び出すと、全部の画像が表示されると思います。
> サンプル画像では無事に表示できたのですが、次に試しに、背景を黒色とした金属部品で
試したのですが、うまくいきませんでした。
考えられる要因を2つ記載しました。
・2値化が上手くできているかを確認してみてください。上手くできていない場合は、2値化のパラメータの調整が必要です。
“`
bin_img = cv2.inRange(hsv, (0, 0, 0), (255, 200, 255))
“`
・サンプルの消しゴムのように対象物に文字や模様など特徴となるものが存在していないと、特徴点抽出がうまくいかない可能性があります。cv2.drawMatches() で特徴点マッチングの結果を可視化できるので、特徴点マッチングが上手くできているかを確認してみてください。
もし可能であれば、どこか参照できる場所に画像をアップロードしていただければ、上手くいかない具体的な原因についてアドバイスできるかと思います。
PyStyleさん
素晴らしい投稿を有難うございます。ここまで具体化したサンプルはなかなか無いと思いました。
やはり画像を変えると2値化の調整、及びそれに依存したcontourの抽出は色々周辺の色合いなどに影響され都度試行錯誤の調整が必要になりますね。お蔭様で当方での画像での確認も一先ず上手く行きました。
この投稿で大分助けられた思いです。改めて有難うございます。
尚、投稿頂いて居る検出例で物体3に対するマッチングの結果画像が物体2と同じになっているかと思います。(本当は二つ目の消しゴムとマッチ)
お手隙の際にご確認頂ければ万全かと思います。
コメントありがとうございます。
お返事が遅くなりすみません。
ご指摘いただいた点を修正しました。