概要
OpenCV の cv2.threshold() で大津の手法による 2 値化を行う方法について解説します。
2 値化の閾値の決め方
画像中の関心がある領域を前景、それ以外の領域を背景としたとき、2 値化の目的は前景の画素と背景の画素を区別できる 2 値画像を作成することです。閾値による 2 値化がうまくいく条件として、入力画像の輝度値の分布が前景と背景で 2 つのグループに分かれている必要があります。
OpenCV での大津の手法
大津の手法で 2 値化するには、cv2.threshold() を使用します。
返り値の ret で大津の手法によって決まった閾値を確認できます。
import cv2
import numpy as np
from IPython.display import display, Image
def imshow(img):
"""ndarray 配列をインラインで Notebook 上に表示する。"""
ret, encoded = cv2.imencode(".jpg", img)
display(Image(encoded))# 画像を読み込む。
img = cv2.imread("sample.jpg")
# グレースケール形式に変換する。
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# 大津の手法
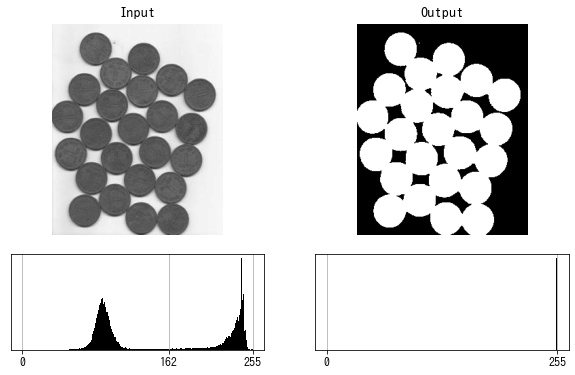
ret, bin_img = cv2.threshold(gray, 10, 255, cv2.THRESH_BINARY_INV + cv2.THRESH_OTSU)
print(f"threshold: {ret}")
imshow(bin_img)threshold: 162.0

大津の手法
画素値 $x_1, x_2, \cdots, x_n$ が与えられたとき、大津の手法では、2 値化をある閾値 $t$ で 2 つのクラス $C_1, C_2$ に線形分離する 2 クラス分類問題として考えます。
画像の画素数を $n$、輝度値 $i$ の画素数を $n_i$ としたとき、輝度値が $i$ である画素の生起確率 $p(i)$ を定義します。
$$ p(i) = \frac{n_i}{n} $$また、クラス $C_1, C_2$ の画素の生起確率を定義します。
$$ \begin{aligned} w_1 &= p(C_1) = \sum_{i = 1}^t p(i) = w(t) \\ w_2 &= p(C_2) = \sum_{i = t + 1}^{L} p(i) = 1 – w(t)\\ \end{aligned} $$クラス内分散の最小化問題として定式化
画像の画素値の平均および分散は
$$ \begin{aligned} \mu_T &= \sum_{i = 0}^L p_i \cdot i \\ \sigma_T^2 &= \sum_{i = 0}^L p_i \cdot (i – \mu_T)^2 \\ \end{aligned} $$クラス $C_1, C_2$ ごとの平均は
$$ \begin{aligned} \mu_1 &= \sum_{i = 1}^t p(i|C_1) \cdot i = \sum_{i = 1}^t \frac{p(i)}{w_1} \cdot i = \frac{\mu(t)}{w(t)} \\ \mu_2 &= \sum_{i = t + 1}^{L} p(i|C_2) \cdot i = \sum_{i = t + 1}^{L} \frac{p(i)}{w_2} \cdot i = \frac{\mu_T – \mu(t)}{1 – w(t)} \\ \end{aligned} $$ただし、
$$ \begin{aligned} w(t) &= \sum_{i = 0}^t p_i \\ \mu(t) &= \sum_{i = 0}^t p_i \cdot i \\ \end{aligned} $$は輝度値 $t \in [0, t]$ の画素の 0 次および 1 次モーメントです。また、
$$ \begin{aligned} \mu_T &= w_1 \mu_1 + w_2 \mu_2 \\ \end{aligned} $$が成り立ちます。
クラス $C_1, C_2$ ごとの分散は
$$ \begin{aligned} \sigma^2_1 &= \sum_{i = 1}^t p(i|C_1) (i – \mu_1)^2 = \sum_{i = 1}^t \frac{p(i)}{w_1} (i – \mu_1)^2 \\ \sigma^2_2 &= \sum_{i = t + 1}^{L} p(i|C_1) (i – \mu_2)^2 = \sum_{i = t + 1}^{L} \frac{p(i)}{w_2} (i – \mu_2)^2 \\ \end{aligned} $$となります。
各クラスの分散 $\sigma_i^2$ の重み付き平均 $\sigma_w^2(t)$ をクラス内分散 (within variance) といいます。
$$ \sigma_w^2(t) = w_1 \sigma_1^2 + w_2 \sigma_2^2 $$大津の手法ではこのクラス内分散を最小化する閾値 $t^*$ を選択します。
$$ t^* = \argmin_t \sigma_w^2(t) $$クラス間分散の最大化問題として定式化
各クラスの平均 $\mu_i$ の重み付き分散 $\sigma_b$ をクラス間分散 (between class variance) といいます。
$$ \begin{aligned} \sigma_b^2(t) &= w_1 (\mu_1 – \mu)^2 + w_2 (\mu_2 – \mu)^2 \end{aligned} $$ここで、
$$ \begin{aligned} \mu_1 – \mu &= \mu_1 – (w_1 \mu_1 + w_2 \mu_2) \\ &= (1 – w_1) \mu_1 – w_2 \mu_2 \\ &= w_2 \mu_1 – w_2 \mu_2 \quad \because w_1 + w_2 = 1 \\ &= w_2 (\mu_1 – \mu_2) \\ \end{aligned} $$同様に
$$ \begin{aligned} \mu_2 – \mu &= \mu_2 – (w_1 \mu_1 + w_2 \mu_2) \\ &= -w_1 \mu_1 + (1 – w_2) \mu_2 \\ &= -w_1 \mu_1 + w_1 \mu_2 \quad \because w_1 + w_2 = 1 \\ &= -w_1 (\mu_1 – \mu_2) \\ \end{aligned} $$よって、
$$ \begin{aligned} \sigma_b^2(t) &= w_1 (\mu_1 – \mu)^2 + w_2 (\mu_2 – \mu)^2 \\ &= w_1 w_2^2 (\mu_1 – \mu_2)^2 + w_2 w_1^2 (\mu_1 – \mu_2)^2 \\ &= w_1 w_2 (w_1 + w_2) (\mu_1 – \mu_2)^2 \\ &= w_1 w_2 (\mu_1 – \mu_2)^2 \quad \because w_1 + w_2 = 1 \\ \end{aligned} $$また
$$ \sigma_T^2 = \sigma_w^2(t) + \sigma_b^2(t) $$が成り立ちます。
これにより、
$$ \begin{aligned} t^* &= \argmin_t \sigma_w^2(t) \\ &= \argmin_t \sigma_T^2 – \sigma_b^2(t) \\ &= \argmax_t \sigma_b^2(t) \\ &= \argmax_t w_1 w_2 (\mu_1 – \mu_2)^2 \\ \end{aligned} $$と変形でき、元の最小化問題では 2 次モーメントを計算する必要がありましたが、この式では 1 次モーメントを計算すればよくなりました。











コメント