目次
概要
連続確率分布の1つであるベータ分布について解説します。
確率密度関数
確率変数 $X$ が次の確率密度関数をもつとき、$X$ はパラメータ $\alpha, \beta$ のベータ分布 (beta distribution) に従うといい、$X \sim Beta(\alpha, \beta)$ と表す。
$$ f_X(x) = \begin{cases} \frac{x^{\alpha – 1} (1 – x)^{\beta – 1}}{\Beta(\alpha, \beta)} & 0 \le x \le 1 \\ 0 & その他の場合 \end{cases} $$ただし、$\Beta(\alpha, \beta)$ はベータ関数で $\alpha > 0, \beta > 0$ とする。
確率関数である
$$ \int_0^1 x^{\alpha – 1} (1 – x)^{\beta – 1} = \frac{\Gamma(\alpha) \Gamma(\beta)}{\Gamma(\alpha + \beta)} $$及び
$$ \frac{\Gamma(\alpha) \Gamma(\beta)}{\Gamma(\alpha + \beta)} = \Beta(\alpha + \beta) $$より、
$$ \int_0^1 \frac{x^{\alpha – 1} (1 – x)^{\beta – 1}}{\Beta(\alpha, \beta)} = 1 $$累積分布関数
$$ \begin{aligned} P(X \le x) &= \int_{-1}^x \frac{t^{\alpha – 1} (1 – t)^{\beta – 1}}{\Beta(\alpha, \beta)} dt \\ &= \frac{\Beta_x(\alpha, \beta)}{\Beta(\alpha, \beta)} \\ &= I_x(\alpha, \beta) \end{aligned} $$ただし、$I_x(\alpha, \beta)$ は正規化された不完全ベータ関数とする。
期待値
$$ \begin{aligned} E[X] &= \int_0^1 x \frac{x^{\alpha – 1} (1 – x)^{\beta – 1}}{\Beta(\alpha, \beta)} dx \\ &= \int_0^1 \frac{x^\alpha (1 – x)^{\beta – 1}}{\Beta(\alpha, \beta)} dx \end{aligned} $$$\alpha’ = \alpha + 1$ とおくと、
$$ \int_0^1 \frac{x^{\alpha’ – 1} (1 – x)^{\beta – 1}}{\Beta(\alpha’ – 1, \beta)} dx $$ここで、ベータ関数の性質
$$ \Beta(\alpha, \beta) = \frac{\alpha + \beta}{\alpha} \Beta(\alpha + 1, \beta) $$より、
$$ \begin{aligned} & \int_0^1 \frac{x^{\alpha’ – 1} (1 – x)^{\beta – 1}}{\Beta(\alpha’ – 1, \beta)} dx \\ &= \frac{\alpha’ – 1}{\alpha’ + \beta – 1} \int_0^1 \frac{x^{\alpha’ – 1} (1 – x)^{\beta – 1}}{\Beta(\alpha’, \beta)} dx \\ &= \frac{\alpha’ – 1}{\alpha’ + \beta – 1} \quad \because 第2項はパラメータ \alpha’, \beta のベータ分布の積分なので1 \\ &= \frac{\alpha}{\alpha + \beta} \quad \because \alpha’ = \alpha + 1 \\ \end{aligned} $$分散
$$ \begin{aligned} E[X] &= \int_0^1 x^2 \frac{x^{\alpha – 1} (1 – x)^{\beta – 1}}{\Beta(\alpha, \beta)} dx \\ &= \int_0^1 \frac{x^{\alpha + 1} (1 – x)^{\beta – 1}}{\Beta(\alpha, \beta)} dx \end{aligned} $$$\alpha’ – 1 = \alpha + 1$ とおくと、
$$ \int_0^1 \frac{x^{\alpha’ – 1} (1 – x)^{\beta – 1}}{\Beta(\alpha’ – 2, \beta)} dx $$ここで、ベータ関数の性質
$$ \Beta(\alpha – 2, \beta) = \frac{\alpha + \beta – 2}{\alpha – 2} \Beta(\alpha – 1, \beta) = \frac{\alpha + \beta – 2}{\alpha – 2} \frac{\alpha + \beta – 1}{\alpha – 1} \Beta(\alpha, \beta) $$より、
$$ \begin{aligned} & \int_0^1 \frac{x^{\alpha’ – 1} (1 – x)^{\beta – 1}}{\Beta(\alpha’ – 2, \beta)} dx \\ &= \frac{\alpha’ – 2}{\alpha’ + \beta – 2} \frac{\alpha’ – 1}{\alpha’ + \beta – 1} \int_0^1 \frac{x^{\alpha’ – 1} (1 – x)^{\beta – 1}}{\Beta(\alpha’, \beta)} dx \\ &= \frac{\alpha’ – 2}{\alpha’ + \beta – 2} \frac{\alpha’ – 1}{\alpha’ + \beta – 1} \quad \because 第2項はパラメータ \alpha’, \beta のベータ分布の積分なので、1 \\ &= \frac{\alpha(\alpha + 1)}{(\alpha + \beta)(\alpha + \beta + 1)} \quad \because \alpha’ – 1 = \alpha + 1 \\ \end{aligned} $$よって、
$$ \begin{aligned} Var[X] &= E[X^2] – (E[X])^2 \\ &= \frac{\alpha(\alpha + 1)}{(\alpha + \beta)(\alpha + \beta + 1)} – \left(\frac{\alpha}{\alpha + \beta}\right)^2 \\ &= \frac{\alpha(\alpha + 1)(\alpha + \beta) – \alpha^2(\alpha + \beta + 1)} {(\alpha + \beta)^2(\alpha + \beta + 1)} \\ &= \frac{\alpha \beta}{(\alpha + \beta)^2(\alpha + \beta + 1)} \end{aligned} $$標準偏差
$$ Std[X] = \sqrt{Var[X]} = \left(\frac{\alpha \beta}{(\alpha + \beta)^2(\alpha + \beta + 1)}\right)^{\frac{1}{2}} $$積率母関数
$$ \begin{aligned} m_X(t) &= E[e^{tX}] \\ &= \int_0^1 e^{tx} f_X(x) dx \\ &= \frac{1}{\Beta(\alpha, \beta)} \int_0^1 \left( \sum_{k = 0}^\infty \frac{(tx)^k}{k!} \right) x^{\alpha – 1} (1 – x)^{\beta – 1} dx \quad \because e^{tx} のテイラー展開 \\ &= \sum_{k = 0}^\infty \frac{t^k}{k!} \frac{1}{\Beta(\alpha, \beta)} \int_0^1 x^{\alpha + k – 1} (1 – x)^{\beta – 1} dx \quad \because 収束半径内で無限級数と積分は交換可能 \\ &= \sum_{k = 0}^\infty \frac{t^k}{k!} \frac{\Beta(\alpha + k, \beta)}{\Beta(\alpha, \beta)} \quad \because ベータ関数の定義 \\ &= 1 + \sum_{k = 1}^\infty \frac{t^k}{k!} \frac{\Beta(\alpha + k, \beta)}{\Beta(\alpha, \beta)} \\ &= 1 + \sum_{k = 1}^\infty \frac{t^k}{k!} \frac{\Gamma(\alpha + k) \Gamma(\beta)}{\Gamma(\alpha + \beta + k)} \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha) \Gamma(\beta)} \quad \because ベータ関数とガンマ関数の関係 \\ &= 1 + \sum_{k = 1}^\infty \frac{t^k}{k!} \frac{\Gamma(\alpha + k)}{\Gamma(\alpha)} \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha + \beta + k)} \\ &= 1 + \sum_{k = 1}^\infty \frac{t^k}{k!} \frac{\Gamma(\alpha) \prod_{r = 0}^{k – 1} (\alpha + r)}{\Gamma(\alpha)} \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha + \beta) \prod_{r = 0}^{k – 1} (\alpha + \beta + r)} \quad \because ガンマ関数の性質 \\ &= 1 + \sum_{k = 1}^\infty \prod_{r = 0}^{k – 1} \left( \frac{\alpha + r}{\alpha + \beta + r} \right) \frac{t^k}{k!} \end{aligned} $$scipy.stats のベータ分布
scipy.stats.beta でベータ分布に従う確率変数を作成できます。
In [1]:
import numpy as np
import seaborn as sns
from matplotlib import pyplot as plt
from scipy.stats import beta
sns.set(style="white")
X = beta(a=2.31, b=0.627)サンプリング
In [2]:
x = X.rvs(size=5)
print(x)[0.99813457 0.5202959 0.95723974 0.92700918 0.8402795 ]
確率密度関数
In [3]:
from itertools import product
import numpy as np
from matplotlib import pyplot as plt
from scipy.stats import beta
fig = plt.figure(figsize=(8, 8))
fig.subplots_adjust(hspace=0.5)
for i, (a, b) in enumerate(product([0.5, 1, 3, 10], [0.5, 1, 3, 10]), 1):
x = np.linspace(0, 1, 100)
y = beta(a, b).pdf(x)
ax = fig.add_subplot(4, 4, i)
ax.set_title(f"a={a}, b={b}")
ax.plot(x, y)
ax.grid()
ax.set_ylim(0, 5)
plt.show()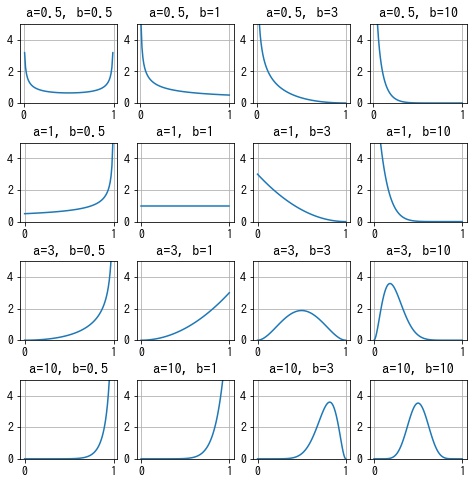
ipywidgets でインタラクティブに密度関数を描画する
In [ ]:
import numpy as np
from ipywidgets import widgets
from matplotlib import pyplot as plt
from scipy.stats import beta
def draw(a, b):
x = np.linspace(0, 1, 100)
y = beta(a, b).pdf(x)
fig, ax = plt.subplots()
ax.plot(x, y)
ax.grid()
ax.set_ylim(0, 5)
plt.show()
slider_a = widgets.FloatSlider(value=1.0, min=0.01, max=10.0, step=0.1)
slider_b = widgets.FloatSlider(value=1.0, min=0.01, max=10.0, step=0.1)
# ウィジェットを表示する。
widgets.interactive(draw, a=slider_a, b=slider_b)統計量
In [4]:
print("mean", X.mean())
print("var", X.var())
print("std", X.std())mean 0.7865168539325842 var 0.04264874077027537 std 0.20651571555277667


コメント