概要
オイラー角による 3 次元の回転表現について解説します。 オイラー角 (Euler Angle)は、3 次元空間における回転の表現方法です。ある座標系から別の座標系への回転を 3 つの回転によって記述します。オイラー角は、航空機やロボット工学、コンピュータビジョンなどの分野で広く使用されます。
オイラー角
3 次元空間における任意の回転は、各軸周りに順次 3 回の回転を行うことで表現できます。このとき、回転する際の角度をオイラー角 (Euler angles) と呼び、$(\alpha, \beta, \gamma)$ や $(\phi, \theta, \psi)$ といった記号で表します。 オイラー角による回転の表現は、回転軸の順番によって異なります。回転軸の順番が $XYZ$ のオイラー角 $\alpha, \beta, \gamma$ と表現した場合、以下を意味します。
- 基底 $(x, y, z)$ を $x$ 軸周りに $\alpha$ だけ回転させ、基底を $(x’, y’, z’)$ に変換する。
- 基底 $(x’, y’, z’)$ を $y’$ 軸周りに $\beta$ だけ回転させ、基底を $(x”, y”, z”)$ に変換する。
- 基底 $(x”, y”, z”)$ を $z”$ 軸周りに $\gamma$ だけ回転させ、基底を $(X, Y, Z)$ に変換する。
例えば、$XYZ$ 軸の順番で回転させる場合と $YXZ$ 軸の順番で回転させる場合とでは、同じ回転を表す場合でもオイラー角は異なります。回転軸の順番は以下の 12 種類が存在します。
- 2 つの軸で回転する場合 (Proper Euler angles)
- $XYX$
- $XZX$
- $YXY$
- $YZY$
- $ZXZ$
- $ZYZ$
- 3 つの軸で回転する場合 (Tait-Bryan angles/roll, pitch, yaw)
- $XYZ$
- $XZY$
- $YXZ$
- $YZX$
- $ZXY$
- $ZYX$
オイラー角 計算・可視化ツール
オイラー角による回転表現を視覚的に理解するためのツールを作成しました。
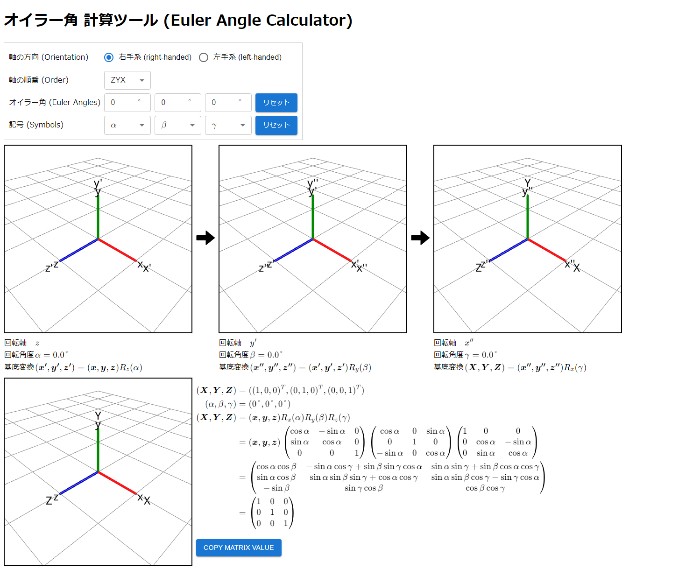
- 以下の情報を表示できます。
- オイラー角が表す回転行列の記号表記を出力
- オイラー角が表す回転行列の数値表記を出力
- 3 回の回転を 3D で可視化
オイラー角から回転行列を作成する
オイラー角による回転表現から、その回転を表す 3×3 の回転行列を作成する手順を紹介します。 回転行列の値については、以下のページで計算できますので、ご活用ください。
右手系の標準基底 $\bm{x} = (1, 0, 0)^T, \bm {y} = (0, 1, 0)^T, \bm {z} = (0, 0, 1)^T$ をとります。 $\bm{x}$ 軸周りに $\theta$ だけ回転させる基底変換行列を $R_x(\theta)$、$\bm{y}$ 軸周りに $\theta$ だけ回転させる基底変換行列を $R_y(\theta)$、$\bm{z}$ 軸周りに $\theta$ だけ回転させる基底変換行列を $R_z(\theta)$ としたとき、例えば、$XYZ$ のオイラー角 $(\alpha, \beta, \gamma)$ が表す基底変換行列 $R$ は、各軸周りの回転を表す基底変換行列を合成することで計算できます。
$$ R = R_x(\alpha)R_y(\beta)R_z(\gamma) $$基底変換行列なので、行列の順番が逆であることに注意してください。 まずは、各軸周りに回転させる基底変換行列を求めます。
x 周りの回転
$\bm{x}$ 周りに角度 $\theta$ だけ回転して得られる基底を $\bm{x}’, \bm{y}’, \bm{z}’$ とする。
このとき、元の基底 $\bm{x}, \bm{y}, \bm{z}$ と変換後の基底 $\bm{x}’, \bm{y}’, \bm{z}’$ の関係は次のようになる。
回転でノルムが変化しないので、$\|\bm{x}\| = \|\bm{y}\| = \|\bm{z}\| = \|\bm{x}’\| = \|\bm{y}’\| = \|\bm{z}’\| = 1$ に注意すると、
$$ \begin{align*} \bm{x}’ &= \bm{x} \\ \bm{y}’ &= \cos\theta \bm{y} + \sin\theta \bm{z} \\ \bm{z}’ &= -\sin\theta \bm{y} + \cos\theta \bm{z} \end{align*} $$よって、基底変換行列は
$$ (\bm{x}’, \bm{y}’, \bm{z}’) = (\bm{x}, \bm{y}, \bm{z}) \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \\ \end{pmatrix} $$y 周りの回転
$\bm{y}$ 周りに角度 $\theta$ だけ回転して得られる基底を $\bm{x}’, \bm{y}’, \bm{z}’$ とする。
このとき、元の基底 $\bm{x}, \bm{y}, \bm{z}$ と変換後の基底 $\bm{x}’, \bm{y}’, \bm{z}’$ の関係は次のようになる。
よって、基底変換行列は
$$ (\bm{x}’, \bm{y}’, \bm{z}’) = (\bm{x}, \bm{y}, \bm{z}) \begin{pmatrix} \cos\theta & 0 & \sin\theta \\ 0 & 1 & 0 \\ -\sin\theta & 0 & \cos\theta \\ \end{pmatrix} $$z 周りの回転
$\bm{z}$ 周りに角度 $\theta$ だけ回転して得られる基底を $\bm{x}’, \bm{y}’, \bm{z}’$ とする。
このとき、元の基底 $\bm{x}, \bm{y}, \bm{z}$ と変換後の基底 $\bm{x}’, \bm{y}’, \bm{z}’$ の関係は次のようになる。
よって、基底変換行列は
$$ (\bm{x}’, \bm{y}’, \bm{z}’) = (\bm{x}, \bm{y}, \bm{z}) \begin{pmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} $$3 つの行列を合成する
例として、XYZ のオイラー角 $(\alpha, \beta, \gamma)$ の回転行列による表現を求めます。
- 基底 $(x, y, z)$ を $x$ 軸周りに $\alpha$ だけ回転させ、基底を $(x’, y’, z’)$ に変換する。
- 基底 $(x’, y’, z’)$ を $y’$ 軸周りに $\beta$ だけ回転させ、基底を $(x”, y”, z”)$ に変換する。
- 基底 $(x”, y”, z”)$ を $z”$ 軸周りに $\gamma$ だけ回転させ、基底を $(X, Y, Z)$ に変換する。
基底 $(x, y, z)$ から基底 $(X, Y, Z)$ に変換する基底変換行列 $R$ は、
$$ \begin{align*} R &= R_x(\alpha)R_y(\beta)R_z(\gamma) \\ &= \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos\alpha & -\sin\alpha \\ 0 & \sin\alpha & \cos\alpha \\ \end{pmatrix} \begin{pmatrix} \cos\beta & 0 & \sin\beta \\ 0 & 1 & 0 \\ -\sin\beta & 0 & \cos\beta \\ \end{pmatrix} \begin{pmatrix} \cos\gamma & -\sin\gamma & 0 \\ \sin\gamma & \cos\gamma & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \\ &= \begin{pmatrix} \cos \beta \cos \gamma & – \sin \gamma \cos \beta & \sin \beta \\ \sin \alpha \sin \beta \cos \gamma + \sin \gamma \cos \alpha & – \sin \alpha \sin \beta \sin \gamma + \cos \alpha \cos \gamma & – \sin \alpha \cos \beta \\ \sin \alpha \sin \gamma – \sin \beta \cos \alpha \cos \gamma & \sin \alpha \cos \gamma + \sin \beta \sin \gamma \cos \alpha & \cos \alpha \cos \beta \end{pmatrix} \end{align*} $$XYZ 以外の順番の回転も同じように求めることができます。
Sympy を使用してオイラー角の回転行列の表現を計算する
Sympy を使用して 12 種類のオイラー角の表現に対応する回転行列を計算します。
import sympy as sy
from IPython.display import display, Math
def Rx(theta):
"""x 軸周りの回転行列"""
return sy.Matrix(
[
[1, 0, 0],
[0, sy.cos(theta), -sy.sin(theta)],
[0, sy.sin(theta), sy.cos(theta)],
]
)
def Ry(theta):
"""y 軸周りの回転行列"""
return sy.Matrix(
[
[sy.cos(theta), 0, sy.sin(theta)],
[0, 1, 0],
[-sy.sin(theta), 0, sy.cos(theta)],
]
)
def Rz(theta):
"""z 軸周りの回転行列"""
return sy.Matrix(
[
[sy.cos(theta), -sy.sin(theta), 0],
[sy.sin(theta), sy.cos(theta), 0],
[0, 0, 1],
]
)
# オイラー角
alpha, beta, gamma = sy.symbols("α β γ")
# 回転軸の順番のパターン
orders = [
["X", "Y", "X"],
["X", "Z", "X"],
["Y", "X", "Y"],
["Y", "Z", "Y"],
["Z", "X", "Z"],
["Z", "Y", "Z"],
["X", "Y", "Z"],
["X", "Z", "Y"],
["Y", "X", "Z"],
["Y", "Z", "X"],
["Z", "X", "Y"],
["Z", "Y", "X"],
]
R = {"X": Rx, "Y": Ry, "Z": Rz}
for axis1, axis2, axis3 in orders:
R1 = R[axis1](alpha)
R2 = R[axis2](beta)
R3 = R[axis3](gamma)
M = R1 @ R2 @ R3
print(f"順番: {axis1}{axis2}{axis3}")
display(Math(sy.latex(M)))順番: XYX
$$ \begin{align*} R &= R_x(\alpha) R_y(\beta) R_x(\gamma) \\ &= \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha \\ 0 & \sin \alpha & \cos \alpha \end{pmatrix} \begin{pmatrix} \cos \beta & 0 & \sin \beta \\ 0 & 1 & 0 \\ -\sin \beta & 0 & \cos \beta \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos \gamma & -\sin \gamma \\ 0 & \sin \gamma & \cos \gamma \end{pmatrix} \\ &= \begin{pmatrix} \cos \beta & \sin \beta \sin \gamma & \sin \beta \cos \gamma \\ \sin \alpha \sin \beta & -\sin \alpha \sin \gamma \cos \beta + \cos \alpha \cos \gamma & -\sin \alpha \cos \beta \cos \gamma -\sin \gamma \cos \alpha \\ -\sin \beta \cos \alpha & \sin \alpha \cos \gamma + \sin \gamma \cos \alpha \cos \beta & -\sin \alpha \sin \gamma + \cos \alpha \cos \beta \cos \gamma \end{pmatrix} \end{align*} $$順番: XZX
$$ \begin{align*} R &= R_x(\alpha) R_z(\beta) R_x(\gamma) \\ &= \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha \\ 0 & \sin \alpha & \cos \alpha \end{pmatrix} \begin{pmatrix} \cos \beta & -\sin \beta & 0 \\ \sin \beta & \cos \beta & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos \gamma & -\sin \gamma \\ 0 & \sin \gamma & \cos \gamma \end{pmatrix} \\ &= \begin{pmatrix} \cos \beta & -\sin \beta \cos \gamma & \sin \beta \sin \gamma \\ \sin \beta \cos \alpha & -\sin \alpha \sin \gamma + \cos \alpha \cos \beta \cos \gamma & -\sin \alpha \cos \gamma -\sin \gamma \cos \alpha \cos \beta \\ \sin \alpha \sin \beta & \sin \alpha \cos \beta \cos \gamma + \sin \gamma \cos \alpha & -\sin \alpha \sin \gamma \cos \beta + \cos \alpha \cos \gamma \end{pmatrix} \end{align*} $$順番: YXY
$$ \begin{align*} R &= R_y(\alpha) R_x(\beta) R_y(\gamma) \\ &= \begin{pmatrix} \cos \alpha & 0 & \sin \alpha \\ 0 & 1 & 0 \\ -\sin \alpha & 0 & \cos \alpha \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos \beta & -\sin \beta \\ 0 & \sin \beta & \cos \beta \end{pmatrix} \begin{pmatrix} \cos \gamma & 0 & \sin \gamma \\ 0 & 1 & 0 \\ -\sin \gamma & 0 & \cos \gamma \end{pmatrix} \\ &= \begin{pmatrix} -\sin \alpha \sin \gamma \cos \beta + \cos \alpha \cos \gamma & \sin \alpha \sin \beta & \sin \alpha \cos \beta \cos \gamma + \sin \gamma \cos \alpha \\ \sin \beta \sin \gamma & \cos \beta & -\sin \beta \cos \gamma \\ -\sin \alpha \cos \gamma -\sin \gamma \cos \alpha \cos \beta & \sin \beta \cos \alpha & -\sin \alpha \sin \gamma + \cos \alpha \cos \beta \cos \gamma \end{pmatrix} \end{align*} $$順番: YZY
$$ \begin{align*} R &= R_y(\alpha) R_z(\beta) R_y(\gamma) \\ &= \begin{pmatrix} \cos \alpha & 0 & \sin \alpha \\ 0 & 1 & 0 \\ -\sin \alpha & 0 & \cos \alpha \end{pmatrix} \begin{pmatrix} \cos \beta & -\sin \beta & 0 \\ \sin \beta & \cos \beta & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} \cos \gamma & 0 & \sin \gamma \\ 0 & 1 & 0 \\ -\sin \gamma & 0 & \cos \gamma \end{pmatrix} \\ &= \begin{pmatrix} -\sin \alpha \sin \gamma + \cos \alpha \cos \beta \cos \gamma & -\sin \beta \cos \alpha & \sin \alpha \cos \gamma + \sin \gamma \cos \alpha \cos \beta \\ \sin \beta \cos \gamma & \cos \beta & \sin \beta \sin \gamma \\ -\sin \alpha \cos \beta \cos \gamma -\sin \gamma \cos \alpha & \sin \alpha \sin \beta & -\sin \alpha \sin \gamma \cos \beta + \cos \alpha \cos \gamma \end{pmatrix} \end{align*} $$順番: ZXZ
$$ \begin{align*} R &= R_z(\alpha) R_x(\beta) R_z(\gamma) \\ &= \begin{pmatrix} \cos \alpha & -\sin \alpha & 0 \\ \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos \beta & -\sin \beta \\ 0 & \sin \beta & \cos \beta \end{pmatrix} \begin{pmatrix} \cos \gamma & -\sin \gamma & 0 \\ \sin \gamma & \cos \gamma & 0 \\ 0 & 0 & 1 \end{pmatrix} \\ &= \begin{pmatrix} -\sin \alpha \sin \gamma \cos \beta + \cos \alpha \cos \gamma & -\sin \alpha \cos \beta \cos \gamma -\sin \gamma \cos \alpha & \sin \alpha \sin \beta \\ \sin \alpha \cos \gamma + \sin \gamma \cos \alpha \cos \beta & -\sin \alpha \sin \gamma + \cos \alpha \cos \beta \cos \gamma & -\sin \beta \cos \alpha \\ \sin \beta \sin \gamma & \sin \beta \cos \gamma & \cos \beta \end{pmatrix} \end{align*} $$順番: ZYZ
$$ \begin{align*} R &= R_z(\alpha) R_y(\beta) R_z(\gamma) \\ &= \begin{pmatrix} \cos \alpha & -\sin \alpha & 0 \\ \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} \cos \beta & 0 & \sin \beta \\ 0 & 1 & 0 \\ -\sin \beta & 0 & \cos \beta \end{pmatrix} \begin{pmatrix} \cos \gamma & -\sin \gamma & 0 \\ \sin \gamma & \cos \gamma & 0 \\ 0 & 0 & 1 \end{pmatrix} \\ &= \begin{pmatrix} -\sin \alpha \sin \gamma + \cos \alpha \cos \beta \cos \gamma & -\sin \alpha \cos \gamma -\sin \gamma \cos \alpha \cos \beta & \sin \beta \cos \alpha \\ \sin \alpha \cos \beta \cos \gamma + \sin \gamma \cos \alpha & -\sin \alpha \sin \gamma \cos \beta + \cos \alpha \cos \gamma & \sin \alpha \sin \beta \\ -\sin \beta \cos \gamma & \sin \beta \sin \gamma & \cos \beta \end{pmatrix} \end{align*} $$順番: XYZ
$$ \begin{align*} R &= R_x(\alpha) R_y(\beta) R_z(\gamma) \\ &= \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha \\ 0 & \sin \alpha & \cos \alpha \end{pmatrix} \begin{pmatrix} \cos \beta & 0 & \sin \beta \\ 0 & 1 & 0 \\ -\sin \beta & 0 & \cos \beta \end{pmatrix} \begin{pmatrix} \cos \gamma & -\sin \gamma & 0 \\ \sin \gamma & \cos \gamma & 0 \\ 0 & 0 & 1 \end{pmatrix} \\ &= \begin{pmatrix} \cos \beta \cos \gamma & -\sin \gamma \cos \beta & \sin \beta \\ \sin \alpha \sin \beta \cos \gamma + \sin \gamma \cos \alpha & -\sin \alpha \sin \beta \sin \gamma + \cos \alpha \cos \gamma & -\sin \alpha \cos \beta \\ \sin \alpha \sin \gamma -\sin \beta \cos \alpha \cos \gamma & \sin \alpha \cos \gamma + \sin \beta \sin \gamma \cos \alpha & \cos \alpha \cos \beta \end{pmatrix} \end{align*} $$順番: XZY
$$ \begin{align*} R &= R_x(\alpha) R_z(\beta) R_y(\gamma) \\ &= \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha \\ 0 & \sin \alpha & \cos \alpha \end{pmatrix} \begin{pmatrix} \cos \beta & -\sin \beta & 0 \\ \sin \beta & \cos \beta & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} \cos \gamma & 0 & \sin \gamma \\ 0 & 1 & 0 \\ -\sin \gamma & 0 & \cos \gamma \end{pmatrix} \\ &= \begin{pmatrix} \cos \beta \cos \gamma & -\sin \beta & \sin \gamma \cos \beta \\ \sin \alpha \sin \gamma + \sin \beta \cos \alpha \cos \gamma & \cos \alpha \cos \beta & -\sin \alpha \cos \gamma + \sin \beta \sin \gamma \cos \alpha \\ \sin \alpha \sin \beta \cos \gamma -\sin \gamma \cos \alpha & \sin \alpha \cos \beta & \sin \alpha \sin \beta \sin \gamma + \cos \alpha \cos \gamma \end{pmatrix} \end{align*} $$順番: YXZ
$$ \begin{align*} R &= R_y(\alpha) R_x(\beta) R_z(\gamma) \\ &= \begin{pmatrix} \cos \alpha & 0 & \sin \alpha \\ 0 & 1 & 0 \\ -\sin \alpha & 0 & \cos \alpha \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos \beta & -\sin \beta \\ 0 & \sin \beta & \cos \beta \end{pmatrix} \begin{pmatrix} \cos \gamma & -\sin \gamma & 0 \\ \sin \gamma & \cos \gamma & 0 \\ 0 & 0 & 1 \end{pmatrix} \\ &= \begin{pmatrix} \sin \alpha \sin \beta \sin \gamma + \cos \alpha \cos \gamma & \sin \alpha \sin \beta \cos \gamma -\sin \gamma \cos \alpha & \sin \alpha \cos \beta \\ \sin \gamma \cos \beta & \cos \beta \cos \gamma & -\sin \beta \\ -\sin \alpha \cos \gamma + \sin \beta \sin \gamma \cos \alpha & \sin \alpha \sin \gamma + \sin \beta \cos \alpha \cos \gamma & \cos \alpha \cos \beta \end{pmatrix} \end{align*} $$順番: YZX
$$ \begin{align*} R &= R_y(\alpha) R_z(\beta) R_x(\gamma) \\ &= \begin{pmatrix} \cos \alpha & 0 & \sin \alpha \\ 0 & 1 & 0 \\ -\sin \alpha & 0 & \cos \alpha \end{pmatrix} \begin{pmatrix} \cos \beta & -\sin \beta & 0 \\ \sin \beta & \cos \beta & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos \gamma & -\sin \gamma \\ 0 & \sin \gamma & \cos \gamma \end{pmatrix} \\ &= \begin{pmatrix} \cos \alpha \cos \beta & \sin \alpha \sin \gamma -\sin \beta \cos \alpha \cos \gamma & \sin \alpha \cos \gamma + \sin \beta \sin \gamma \cos \alpha \\ \sin \beta & \cos \beta \cos \gamma & -\sin \gamma \cos \beta \\ -\sin \alpha \cos \beta & \sin \alpha \sin \beta \cos \gamma + \sin \gamma \cos \alpha & -\sin \alpha \sin \beta \sin \gamma + \cos \alpha \cos \gamma \end{pmatrix} \end{align*} $$順番: ZXY
$$ \begin{align*} R &= R_z(\alpha) R_x(\beta) R_y(\gamma) \\ &= \begin{pmatrix} \cos \alpha & -\sin \alpha & 0 \\ \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos \beta & -\sin \beta \\ 0 & \sin \beta & \cos \beta \end{pmatrix} \begin{pmatrix} \cos \gamma & 0 & \sin \gamma \\ 0 & 1 & 0 \\ -\sin \gamma & 0 & \cos \gamma \end{pmatrix} \\ &= \begin{pmatrix} -\sin \alpha \sin \beta \sin \gamma + \cos \alpha \cos \gamma & -\sin \alpha \cos \beta & \sin \alpha \sin \beta \cos \gamma + \sin \gamma \cos \alpha \\ \sin \alpha \cos \gamma + \sin \beta \sin \gamma \cos \alpha & \cos \alpha \cos \beta & \sin \alpha \sin \gamma -\sin \beta \cos \alpha \cos \gamma \\ -\sin \gamma \cos \beta & \sin \beta & \cos \beta \cos \gamma \end{pmatrix} \end{align*} $$順番: ZYX
$$ \begin{align*} R &= R_z(\alpha) R_y(\beta) R_x(\gamma) \\ &= \begin{pmatrix} \cos \alpha & -\sin \alpha & 0 \\ \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} \cos \beta & 0 & \sin \beta \\ 0 & 1 & 0 \\ -\sin \beta & 0 & \cos \beta \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos \gamma & -\sin \gamma \\ 0 & \sin \gamma & \cos \gamma \end{pmatrix} \\ &= \begin{pmatrix} \cos \alpha \cos \beta & -\sin \alpha \cos \gamma + \sin \beta \sin \gamma \cos \alpha & \sin \alpha \sin \gamma + \sin \beta \cos \alpha \cos \gamma \\ \sin \alpha \cos \beta & \sin \alpha \sin \beta \sin \gamma + \cos \alpha \cos \gamma & \sin \alpha \sin \beta \cos \gamma -\sin \gamma \cos \alpha \\ -\sin \beta & \sin \gamma \cos \beta & \cos \beta \cos \gamma \end{pmatrix} \end{align*} $$左手系の場合
左手系の場合 $\bm{y}$ が反転します。また、正の回転を時計回りと規定します。 右手系と同じ考え方で基底変換行列を求めると、$\bm{x}$ 軸周り、$\bm{y}$ 軸周り、$\bm{z}$ 軸周りの回転を表す基底変換行列は、いずれも右手系と同じになります。
ロール・ピッチ・ヨー
オイラー角の回転を、ロール (roll)、ピッチ (pitch)、ヨー (yaw) で表現することもあります。 この場合、x 軸周りの回転を roll、y 軸周りの回転を pitch、z 軸周りの回転を yaw といます。


コメント