MENU

統計学 – t 分布

数学
数学 機械学習 統計学
  1. ホーム
  2. 数学
  3. 統計学 – t 分布
目次
  1. 概要
  2. t 分布
  3. 確率関数
  4. 確率密度関数の導出
  5. 期待値
  6. 分散
  7. 標準偏差
  8. scipy.stats の t 分布
    1. サンプリング
    2. 確率密度関数
    3. 累積分布関数
    4. 統計量

概要

連続確率分布の1つであるt分布について解説します。

t 分布

確率変数 XX が自由度 nn のカイ二乗分布に従い、環境変数 ZZ が標準正規分布に従うとし、X,YX, Y は独立であるとする。このとき、

Y=ZXn Y = \frac{Z}{\sqrt{\frac{X}{n}}}

は自由度 nn の t 分布 (t distribution) に従うという。 確率変数 XX が自由度 nn の t 分布に従うとき、Y∼tnY \sim t_n と表す。

確率関数

確率変数 YY が t 分布に従う確率変数のとき、確率密度関数は

fY(y)=Γ[n+12]nπΓ(n2)[1+y2n]−n+12,y∈R f_Y(y) = \frac{\Gamma \left[ \frac{n + 1}{2} \right]}{\sqrt{n \pi} \Gamma(\frac{n}{2})} \left[ 1 + \frac{y^2}{n} \right]^{- \frac{n + 1}{2}} , y \in \R

ただし、Γ(⋅)\Gamma(\cdot) はガンマ関数、n∈Nn \in \N とする。

確率密度関数の導出

結合確率密度関数は

fX,Z(x,z)=12πexp⁡(–z22)⋅1Γ(n2)2n2xn2–1e−x2∵X,Zは独立 \begin{aligned} f_{X, Z}(x, z) &= \frac{1}{\sqrt{2 \pi}} \exp \left( – \frac{z^2}{2} \right) \cdot \frac{1}{\Gamma \left( \frac{n}{2} \right) 2^{\frac{n}{2}}} x^{\frac{n}{2} – 1} e^{- \frac{x}{2}} \quad \because X, Z は独立 \end{aligned}

ここで、Y=ZXn,V=XY = \frac{Z}{\sqrt{\frac{X}{n}}}, V = X の変数変換をすると、

{y=zxnv=x⇔{z=vnyx=v \begin{cases} y = \frac{z}{\sqrt{\frac{x}{n}}} \\ v = x \end{cases} \Leftrightarrow \begin{cases} z = \sqrt{\frac{v}{n}} y \\ x = v \end{cases}

ヤコビアンは

∣∂z∂y∂z∂v∂x∂y∂x∂v∣=∣vny2nv01∣=vn \begin{vmatrix} \frac{\partial z}{\partial y} & \frac{\partial z}{\partial v} \\ \frac{\partial x}{\partial y} & \frac{\partial x}{\partial v} \\ \end{vmatrix} = \begin{vmatrix} \sqrt{\frac{v}{n}} & \frac{y}{2 \sqrt{nv}} \\ 0 & 1 \\ \end{vmatrix} = \sqrt{\frac{v}{n}}

また、−∞<y<∞,0<v<∞-\infty < y < \infty, 0 < v < \infty

よって、

fY,V(y,v)=12πexp⁡(–vy22n)⋅1Γ(n2)2n2vn2–1e−v2vn=1Γ(n2)2n22πnexp⁡(–v2(y2n+1))vn2–1+12 \begin{aligned} f_{Y, V}(y, v) &= \frac{1}{\sqrt{2 \pi}} \exp \left( – \frac{v y^2}{2n} \right) \cdot \frac{1}{\Gamma \left( \frac{n}{2} \right) 2^{\frac{n}{2}}} v^{\frac{n}{2} – 1} e^{- \frac{v}{2}} \sqrt{\frac{v}{n}} \\ &= \frac{1}{\Gamma \left( \frac{n}{2} \right) 2^{\frac{n}{2}} \sqrt{2 \pi n}} \exp \left( – \frac{v}{2} \left(\frac{y^2}{n} + 1\right) \right) v^{\frac{n}{2} – 1 + \frac{1}{2}} \\ \end{aligned}

YY の周辺確率密度関数は

fY(y)=∫−∞∞fY,V(y,v)dv=K∫0∞exp⁡(–v2(y2n+1))vn+12–1dv \begin{aligned} f_Y(y) &= \int_{-\infty}^\infty f_{Y, V}(y, v) dv \\ &= K \int_0^\infty \exp \left( – \frac{v}{2} \left(\frac{y^2}{n} + 1\right) \right) v^{\frac{n + 1}{2} – 1} dv \\ \end{aligned}

ただし、

K=1Γ(n2)2n22πn K = \frac{1}{\Gamma \left( \frac{n}{2} \right) 2^{\frac{n}{2}} \sqrt{2 \pi n}}

とおいた。

ここで、t=v2(y2n+1)t = \frac{v}{2} \left(\frac{y^2}{n} + 1\right) とおくと、v=2ny2+ntv = \frac{2n}{y^2 + n} t、dv=2ny2+ndtdv = \frac{2n}{y^2 + n} dt より、

∫0∞e−t(2ny2+nt)n+12–12ny2+ndt=(2ny2+n)n+12∫0∞tn+12–1e−tdt=(2ny2+n)n+12Γ(n+12)∵ガンマ関数の定義 \begin{aligned} & \int_0^\infty e^{-t} \left( \frac{2n}{y^2 + n} t \right)^{\frac{n + 1}{2} – 1} \frac{2n}{y^2 + n} dt \\ &= \left( \frac{2n}{y^2 + n} \right)^{\frac{n + 1}{2}} \int_0^\infty t^{\frac{n + 1}{2} – 1} e^{-t} dt \\ &= \left( \frac{2n}{y^2 + n} \right)^{\frac{n + 1}{2}} \Gamma\left( \frac{n + 1}{2} \right) \quad \because ガンマ関数の定義 \end{aligned}

以上より、

fY(y)=1Γ(n2)2n22πn(2ny2+n)n+12Γ(n+12)=Γ(n+12)Γ(n2)πn(y2n+1)−n+12,−∞<y<∞ \begin{aligned} f_Y(y) &= \frac{1}{\Gamma \left( \frac{n}{2} \right) 2^{\frac{n}{2}} \sqrt{2 \pi n}} \left( \frac{2n}{y^2 + n} \right)^{\frac{n + 1}{2}} \Gamma\left( \frac{n + 1}{2} \right) \\ &= \frac{\Gamma\left( \frac{n + 1}{2} \right) }{\Gamma \left( \frac{n}{2} \right) \sqrt{\pi n}} \left( \frac{y^2}{n} + 1 \right)^{-\frac{n + 1}{2}}, -\infty < y < \infty\\ \end{aligned}

期待値

n>1n > 1 のとき、

E[Y]=E[ZXn]=nE[ZX]=nE[1X]E[Z]∵X,Zは独立=0∵E[Z]=0 \begin{aligned} E[Y] &= E\left[\frac{Z}{\sqrt{\frac{X}{n}}} \right] \\ &= \sqrt{n} E\left[\frac{Z}{\sqrt{X}} \right] \\ &= \sqrt{n} E\left[\frac{1}{\sqrt{X}}\right] E[Z] \quad \because X, Z は独立 \\ &= 0 \quad \because E[Z] = 0 \end{aligned}

分散

n>2n > 2 のとき、

E[Y2]=E[Z2Xn]=nE[Z2X]=nE[1X]E[Z2]∵X,Zは独立 \begin{aligned} E[Y^2] &= E\left[\frac{Z^2}{\frac{X}{n}} \right] \\ &= n E\left[\frac{Z^2}{X} \right] \\ &= n E\left[\frac{1}{X}\right] E[Z^2] \quad \because X, Z は独立 \end{aligned}

ここで、X∼χn2X \sim \chi_n^2 より、

E[1X]=1n–2 E\left[\frac{1}{X}\right] = \frac{1}{n – 2}

Z2∼χ12Z^2 \sim \chi_1^2 より、

E[Z2]=1 E[Z^2] = 1

よって、

E[Y2]=nE[1X]E[Z2]=nn–2 \begin{aligned} E[Y^2] &= n E\left[\frac{1}{X}\right] E[Z^2] \\ &= \frac{n}{n – 2} \end{aligned}

したがって、分散は

Var[Y]=E[Y2]–(E[Y])2=nn–2 \begin{aligned} Var[Y] &= E[Y^2] – (E[Y])^2 \\ &= \frac{n}{n – 2} \\ \end{aligned}

標準偏差

Std[X]=Var[X]=nn–2 \begin{aligned} Std[X] &= \sqrt{Var[X]} \\ &= \sqrt{\frac{n}{n – 2}} \end{aligned}

scipy.stats の t 分布

scipy.stats.t で t 分布に従う確率変数を作成できます。

In [1]: 
import numpy as np
import seaborn as sns
from matplotlib import pyplot as plt
from scipy.stats import t

sns.set(style="white")

df = 2.74
X = t(df)
Python

サンプリング

In [2]: 
x = X.rvs(size=5)
print(x)
Python
[-0.30791396  0.34077362 -2.2863223  -1.55023673  1.40032404]

確率密度関数

In [3]: 
x = np.linspace(-5, 5, 100)
y = X.pdf(x)

fig, ax = plt.subplots()
ax.plot(x, y)
ax.grid()

plt.show()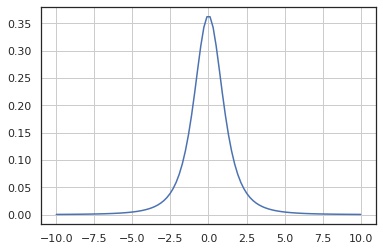
Python

累積分布関数

In [4]: 
x = np.linspace(-5, 5, 100)
y = X.cdf(x)

fig, ax = plt.subplots()
ax.plot(x, y)
ax.grid()

plt.show()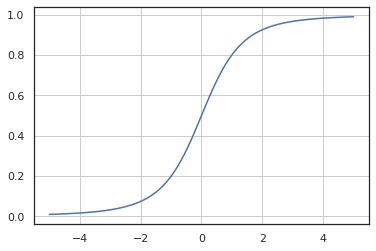
Python

統計量

In [5]: 
print("mean", X.mean())
print("var", X.var())
print("std", X.std())
Python
mean 0.0
var 3.7027027027027017
std 1.924240812035412
数学
数学 機械学習 統計学

コメント

コメントする

目次
  1. 概要
  2. t 分布
  3. 確率関数
  4. 確率密度関数の導出
  5. 期待値
  6. 分散
  7. 標準偏差
  8. scipy.stats の t 分布
    1. サンプリング
    2. 確率密度関数
    3. 累積分布関数
    4. 統計量