Warning: Undefined variable $position in /home/pystyles/pystyle.info/public_html/wp/wp-content/themes/lionblog/functions.php on line 4897
  1. HOME
  2. 数学
  3. 統計学 - 非心カイ二乗分布

統計学 – 非心カイ二乗分布

統計学 – 非心カイ二乗分布
目次

概要

連続確率分布の1つである非心カイ二乗分布について解説します。

Advertisement

非心カイ二乗分布

確率変数 $X_1, X_2, \cdots, X_n$ が独立でそれぞれ平均 $\mu_i$、分散 $1$ の正規分布に従うとき、$Y = X_1^2 + X_2^2 + \cdots + X_n^2$ は非心度 $\delta = \mu_1^2 + \mu_2^2 + \cdots + \mu_n^2$、自由度 $n$ の非心カイ二乗分布に従う。

積率母関数

確率変数 $X_1, X_2, \cdots, X_n$ が独立でそれぞれ平均 $\mu_i$、分散 $1$ の正規分布に従うとし、$Y = X_1^2 + X_2^2 + \cdots + X_n^2$ とする。

$$ \begin{aligned} m_Y(t) &= E[e^{tY}] \\ &= E\left[ \exp \left(t \sum_{i = 1}^n X_i^2 \right) \right] \\ &= E\left[ \prod_{i = 1}^n \exp \left(t X_i^2 \right) \right] \\ \end{aligned} $$

ここで、

$$ \begin{aligned} & E\left[ \prod_{i = 1}^n \exp \left(t X_i^2 \right) \right] \\ &= \int_{-\infty}^\infty t x_i^2 \frac{1}{\sqrt{2 \pi}} \exp \left( – \frac{(x_i – \mu_i)^2}{2} \right) dx_i \\ &= \int_{-\infty}^\infty \frac{1}{\sqrt{2 \pi}} \exp \left( t x_i^2 – \frac{(x_i – \mu_i)^2}{2} \right) dx_i \\ &= \int_{-\infty}^\infty \frac{1}{\sqrt{2 \pi}} \exp \left(\frac{1}{2} (-(1 – 2 t) x_i^2 + 2 x \mu – \mu^2) \right) dx_i \\ &= \int_{-\infty}^\infty \frac{1}{\sqrt{2 \pi}} \exp \left( \frac{1}{2} \left( -(1 – 2 t) \left(x_i – \frac{\mu_i}{1 – 2 t}\right)^2 – \mu_i^2 + \frac{\mu_i^2}{1 – 2t} \right) \right) dx_i \quad \because 平方完成 \\ &= \int_{-\infty}^\infty \frac{1}{\sqrt{2 \pi}} \exp \left( -\frac{1 – 2 t}{2} \left(x_i – \frac{\mu_i}{1 – 2 t}\right)^2 + \frac{t \mu_i^2}{1 – 2t} \right) dx_i \\ &= \exp(\frac{t \mu_i^2}{1 – 2t}) \int_{-\infty}^\infty \frac{1}{\sqrt{2 \pi}} \exp \left(-\frac{1 – 2 t}{2} \left(x_i – \frac{\mu_i}{1 – 2 t}\right)^2 \right) dx_i \\ &= \exp(\frac{t \mu_i^2}{1 – 2t}) \frac{1}{\sqrt{1 – 2t}} \int_{-\infty}^\infty \frac{\sqrt{1 – 2t}}{\sqrt{2 \pi}} \exp \left(-\frac{1 – 2 t}{2} \left(x_i – \frac{\mu_i}{1 – 2 t}\right)^2 \right) dx_i \\ &= \exp \left(\frac{t \mu_i^2}{1 – 2t} \right) \frac{1}{\sqrt{1 – 2t}} \int_{-\infty}^\infty f(x_i) dx_i \quad \because t < \frac{1}{2} のとき、平均 \frac{\mu_i}{1 – 2t}、分散 \frac{1}{1 – 2t} の正規分布 \\ &= \exp \left(\frac{t \mu_i^2}{1 – 2t} \right) \left( \frac{1}{1 – 2t} \right)^\frac{1}{2} \end{aligned} $$

よって、

$$ \begin{aligned} m_Y(t) &= E\left[ \prod_{i = 1}^n \exp \left(t X_i^2 \right) \right] \\ &= \exp \left(\frac{t \sum_{i = 1}^n \mu_i^2}{1 – 2t} \right) \left( \frac{1}{1 – 2t} \right)^\frac{n}{2}, t < \frac{1}{2} \end{aligned} $$

確率関数

確率変数 $X$ が次の確率密度関数をもつとき、$X$ は非心度 (noncentral parameter) $\delta$、自由度 $n$ の非心カイ二乗分布 (noncentral chi squared distribution) または非心 $\chi^2$ 分布に従うという。

確率変数 $X$ が非心度 $\delta$、自由度 $n$ の非心カイ二乗分布に従うとき、$X \sim \chi_n^2(\delta)$ と表す。

$$ \begin{aligned} f_X(x) &= \begin{cases} \displaystyle f_X(x) = \sum_{k = 0}^\infty \frac{e^{-\frac{\delta}{2}} (\frac{\delta}{2})^k}{k!} \frac{1} {2^{\frac{n}{2} + k} \Gamma \left(\frac{n}{2} + k\right)} x^{\frac{n}{2} + k – 1} e^{- \frac{x}{2}} & x > 0 \\ 0 & その他の場合 \end{cases} \\ \end{aligned} $$

ただし、$\Gamma(\cdot)$ はガンマ関数、$n \in \N, \delta \ge 0$ とする。

$f_{2_k + n}(x)$ を自由度 $2k + n$ のカイ二乗分布の確率密度関数とすると、

$$ \begin{aligned} f_X(x) &= \begin{cases} \displaystyle f_X(x) = e^{-\frac{\delta}{2}} \sum_{k = 0}^\infty \frac{ (\frac{\delta}{2})^k}{k!} f_{2k + n}(x) & x > 0 \\ 0 & その他の場合 \end{cases} \\ \end{aligned} $$

とかける。

期待値

$X_i \sim N(\mu_i, 1)$ なので、$E[X_i^2] = \mu_i^2 + 1$ に注意すると、

$$ \begin{aligned} E[Y] &= E[X_1^2 + \cdots + X_n^2] \\ &= \sum_{i = 1}^n E[X_i^2] \\ &= \sum_{i = 1}^n (\mu_i^2 + 1) \\ &= \sum_{i = 1}^n \mu_i^2 + n \\ &= \delta + n \\ \end{aligned} $$

分散

$X_i \sim N(\mu_i, 1)$ のとき、正規分布の中心積率 より $E[(X_i – \mu_i)^4] =3, E[(X_i – \mu_i)^2] = 1$ なので、

$$ \begin{aligned} Var[(X_i – \mu_i)^2] &= E[(X_i – \mu_i)^4] – (E[(X_i – \mu_i)^2])^2 \\ &= 3 – 1 \quad \because 正規分布の k 次の中心積率 \\ &= 2 \end{aligned} $$

に注意すると、

$$ \begin{aligned} Var[Y] &= Var[X_1^2 + \cdots + X_n^2] \\ &= \sum_{i = 1}^n Var[X_i^2] \quad \because X_1, X_2, \cdots, X_n は独立 [1] \\ &= \sum_{i = 1}^n Var[(X_i – \mu_i)^2 + 2 \mu_i (X_i – \mu_i) + \mu_i^2] \\ &= \sum_{i = 1}^n (Var[(X_i – \mu_i)^2] + Var[2 \mu_i (X_i – \mu_i)]) \quad \because (X_i – \mu_i)^2, X_i – \mu_i は独立 \\ &= \sum_{i = 1}^n Var[(X_i – \mu_i)^2] + \sum_{i = 1}^n 4 \mu_i^2 Var[X_i – \mu_i] \\ &= 2n + 4 \sum_{i = 1}^n \mu_i^2 \quad \because Var[X_i – \mu_i] = Var[X_i] = 1 \\ &= 2n + 4 \delta \\ \end{aligned} $$

標準偏差

$$ Std[X] = \sqrt{Var[X]} = \sqrt{2n + 4 \delta} $$
Advertisement

scipy.stats の非心カイ二乗分布

scipy.stats.ncx2 で非心カイ二乗分布に従う確率変数を作成できます。

In [1]: 
import numpy as np
import seaborn as sns
from matplotlib import pyplot as plt
from scipy.stats import ncx2

sns.set(style="white")

df, nc = 21, 1.06
X = ncx2(21, 1.06)

サンプリング

In [2]: 
x = X.rvs(size=5)
print(x)
[15.41757792 23.61434967 27.98127105 22.85990679 37.43546455]

確率密度関数

In [3]: 
x = np.linspace(0.01, 50, 100)
y = X.pdf(x)

fig, ax = plt.subplots()
ax.plot(x, y)
ax.grid()

plt.show()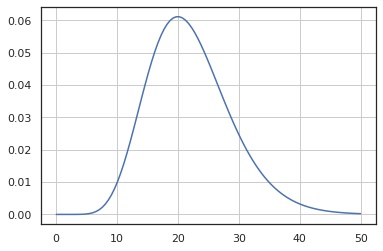

累積分布関数

In [4]: 
x = np.linspace(0.01, 50, 100)
y = X.cdf(x)

fig, ax = plt.subplots()
ax.plot(x, y)
ax.grid()

plt.show()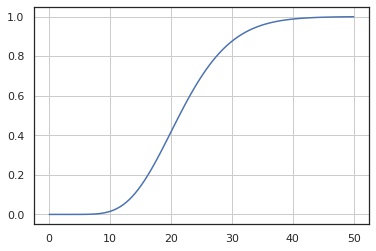

統計量

In [5]: 
print("mean", X.mean())
print("var", X.var())
print("std", X.std())
mean 22.06
var 46.24
std 6.8