Warning: Undefined variable $position in /home/pystyles/pystyle.info/public_html/wp/wp-content/themes/lionblog/functions.php on line 4897
  1. HOME
  2. 数学
  3. 統計学 - 正規分布

統計学 – 正規分布

統計学 – 正規分布
目次

概要

連続確率分布の1つである正規分布について解説します。

Advertisement

確率密度関数

確率変数 $X$ が次のような確率密度関数をもつとき、$X$ はパラメータ $\mu, \sigma^2$ の正規分布 (normal distribution) またはガウス分布 (Gaussian distribution) に従うという。 確率変数 $X$ がパラメータ $\mu, \sigma^2$ の正規分布に従うとき、$X \sim N(\mu, \sigma^2)$ と表す。

$$ f_X(x) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left( -\frac{(x – \mu)^2}{2 \sigma^2} \right), x \in \mathbb{R} $$

確率密度関数の要件を満たしている

$$ \begin{aligned} \int_{-\infty}^{\infty} \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left( -\frac{(x – \mu)^2}{2 \sigma^2} \right) dx &= \int_{-\infty}^\infty \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left( -\frac{(t – \mu)^2}{2 \sigma^2} \right) dt \\ &= \frac{1}{\sqrt{2 \pi} \sigma} \int_{-\infty}^\infty \exp(-u^2) \sqrt{2} \sigma du \quad \because u = \frac{t – \mu}{\sqrt{2} \sigma} と置換積分 \\ &= \frac{1}{\sqrt{\pi}} \int_{-\infty}^\infty \exp(-u^2) du \quad \because ガウス積分 \\ &= \frac{1}{\sqrt{\pi}} \sqrt{\pi} \\ &= 1 \end{aligned} $$

累積確率関数

$$ \begin{aligned} P(X \le x) &= \int_{-\infty}^x \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left( -\frac{(t – \mu)^2}{2 \sigma^2} \right) dt \\ &= \frac{1}{\sqrt{2 \pi} \sigma} \int_{-\infty}^\frac{x – \mu}{\sqrt{2} \sigma} \exp(-u^2) \sqrt{2} \sigma du \quad \because u = \frac{t – \mu}{\sqrt{2} \sigma} と置換積分 \\ &= \frac{1}{\sqrt{\pi}} \int_{-\infty}^\frac{x – \mu}{\sqrt{2} \sigma} \exp(-u^2) du \\ &= \frac{1}{\sqrt{\pi}} \left( \int_{-\infty}^0 \exp(-u^2) du + \int_{0}^\frac{x – \mu}{\sqrt{2} \sigma} \exp(-u^2) du \right) \\ &= \frac{1}{\sqrt{\pi}} \left( \frac{\sqrt{\pi}}{2} + \int_{0}^\frac{x – \mu}{\sqrt{2} \sigma} \exp(-u^2) du \right) \quad \because ガウス積分 \\ &= \frac{1}{2} + \frac{1}{2} \frac{2}{\sqrt{\pi}} \int_{0}^\frac{x – \mu}{\sqrt{2} \sigma} \exp(-u^2) du \\ &= \frac{1}{2} \left(1 + \text{erf}\left(\frac{x – \mu}{\sqrt{2} \sigma}\right) \right) \quad \because \text{erf} の定義 \\ \end{aligned} $$

期待値

$$ \begin{aligned} E[X] &= \frac{1}{ \sigma \sqrt{2 \pi}} \int_{-\infty}^\infty x \exp \left( -\frac{(x – \mu)^2}{2 \sigma^2} \right) dx \\ &= \frac{\sqrt{2} \sigma}{\sqrt{2 \pi} \sigma} \int_{-\infty}^\infty (\sqrt{2} \sigma t + \mu) \exp \left( -t^2 \right) dx \quad \because t = \dfrac {x – \mu} {\sqrt 2 \sigma} で置換積分 \\ &= \frac{1}{\sqrt{\pi}} \left( \sqrt{2} \sigma \int_{-\infty}^\infty t \exp(-t^2) dt + \mu \int_{-\infty}^\infty \exp(-t^2) dt \right) \\ &= \frac{1}{\sqrt{\pi}} \left( \sqrt{2} \sigma \cdot 0 + \mu \sqrt{\pi} \right) \quad \because ガウス積分 \\ &= \mu \end{aligned} $$

分散

$$ \begin{aligned} E[X^2] &= \frac{1}{ \sigma \sqrt{2 \pi}} \int_{-\infty}^\infty x^2 \exp \left( -\frac{(x – \mu)^2}{2 \sigma^2} \right) dx \\ &= \frac{\sqrt{2} \sigma}{\sqrt{2 \pi} \sigma} \int_{-\infty}^\infty (\sqrt{2} \sigma t + \mu)^2 \exp \left( -t^2 \right) dx \quad \because t = \dfrac {x – \mu} {\sqrt 2 \sigma} で置換積分 \\ &= \frac{1}{\sqrt{\pi}} \left( 2 \sigma^2 \int_{-\infty}^\infty t^2 \exp(-t^2) dt + 2 \sqrt{2} \sigma \mu \int_{-\infty}^\infty t \exp(-t^2) dt + \mu^2 \int_{-\infty}^\infty \exp(-t^2) dt \right) \\ &= \frac{1}{\sqrt{\pi}} \left( 2 \sigma^2 \frac{\sqrt{\pi}}{2} + 2 \sqrt{2} \sigma \mu \cdot 0 + \mu^2 \sqrt{\pi} \right) \\ &= \sigma^2 + \mu^2 \end{aligned} $$

よって、分散は

$$ \begin{aligned} Var[X] &= E[X^2] – (E[X])^2 \\ &= \sigma^2 + \mu^2 – \mu^2 \\ &= \sigma^2 \end{aligned} $$
Advertisement

標準偏差

$$ Std[X]= \sqrt{Var[X]} = \sigma $$

積率母関数

$$ \begin{aligned} m_X(t) &= E[e^{tX}] \\ &= \frac{1}{\sqrt{2 \pi} \sigma} \int_{-\infty}^\infty e^{tx} \exp \left( -\frac{(x – \mu)^2}{2 \sigma^2} \right) dx \\ &= \frac{1}{\sqrt{2 \pi} \sigma} \int_{-\infty}^\infty \exp \left( tx -\frac{(x – \mu)^2}{2 \sigma^2} \right) dx \\ &= \exp \left(\mu t + \frac{\sigma^2 t^2}{2} \right) \int_{-\infty}^\infty \frac{1}{\sqrt{2 \pi} \sigma} \exp \left( -\frac{(x – (\mu + \sigma^2 t))^2}{2 \sigma^2} \right) dx \\ &= \exp \left(\mu t + \frac{\sigma^2 t^2}{2} \right) \int_{-\infty}^\infty f_X(x) dx \quad \because パラメータ \mu + \sigma^2 t, \sigma^2 の正規分布 \\ &= \exp \left(\mu t + \frac{\sigma^2 t^2}{2} \right) \end{aligned} $$

正規分布のk次の中心積率

$X \sim N(\mu, \sigma^2)$ のとき、

$$ E[(X – \mu)^k] = \begin{cases} (k – 1)!! \sigma^{k} = ((k – 1)(k – 3) \cdots 1) \sigma^{k} & k = 2, 4, \cdots \\ 0 & k = 1, 3, \cdots \\ \end{cases} $$

例:

$$ \begin{aligned} E[(X – \mu)^2] &= 1 \\ E[(X – \mu)^4] &= 3 \end{aligned} $$

証明:

積率母関数の定義より、

$$ \begin{aligned} m_{X – \mu}(t) &= E[\exp((X – \mu)t)] \\ &= E \left[ \sum_{k = 0}^\infty \frac{\left((X – \mu)t \right)^k}{k!} \right] \quad \because マクローリン展開 \\ &= \sum_{k = 0}^\infty E[(X – \mu)^k] \frac{t^k}{k!} \quad (1) \\ \end{aligned} $$

他方、$X – \mu \sim N(0, \sigma^2)$ であるから、正規分布の積率母関数に当てはめると、

$$ \begin{aligned} m_{X – \mu}(t) &= \exp \left(\frac{\sigma^2 t^2}{2} \right) \\ &= \sum_{k = 0}^\infty \frac{\left(\frac{\sigma^2 t^2}{2} \right)^k}{k!} \quad \because マクローリン展開 \\ &= \sum_{k = 0}^\infty \frac{\sigma^{2k} t^{2k}}{2^k k!} \quad (2) \end{aligned} $$

両者の式の係数を比較すると、

$k$ が奇数のとき、$E[(X – \mu)^k] = 0$
$k$ が偶数のとき、(1) における $k = 2n$ としたときの $t^{2n}$ の係数 $\frac{E[(X – \mu)^{2n}]}{2n!}$ と、(2) における $t^{2n}$ の係数 $\frac{\sigma^{2n}}{2^n n!}$ が同じなので、

$$ \begin{aligned} \frac{E[(X – \mu)^{2n}]}{2n!} &= \frac{\sigma^{2n}}{2^n n!} \\ E[(X – \mu)^{2n}] &= \frac{2n!}{2^n n!} \sigma^{2n} \\ \end{aligned} $$

$2^n n! = 2n \cdot 2 (n – 1) \cdots (2 \cdot 1) = 2n \cdot (2n – 2) \cdot 2$ に注意すると、

$$ \begin{aligned} E[(X – \mu)^{2n}] &= \frac{2n!}{2^n n!} \sigma^{2n} \\ &= \frac{2n \cdot (2n – 1) \cdot (2n – 2) \cdots 2 \cdot 1}{2n \cdot (2n – 2) \cdot 2} \sigma^{2n} \\ &= ((2n – 1) \cdot (2n – 3) \cdots 3 \cdot 1) \sigma^{2n} \\ &= (2n – 1)!! \sigma^{2n} \\ \end{aligned} $$

scipy.stats の正規分布

scipy.stats.norm で正規分布に従う確率変数を作成できます。

In [1]: 
import numpy as np
import seaborn as sns
from matplotlib import pyplot as plt
from scipy.stats import norm

sns.set(style="white")

X = norm()

サンプリング

In [2]: 
x = X.rvs(size=5)
print(x)
[ 0.49353417  1.45683727 -2.78100417 -0.28630157 -0.79504348]

確率密度関数

In [3]: 
x = np.linspace(-10, 10, 100)
y = X.pdf(x)

fig, ax = plt.subplots()
ax.plot(x, y)
ax.grid()

plt.show()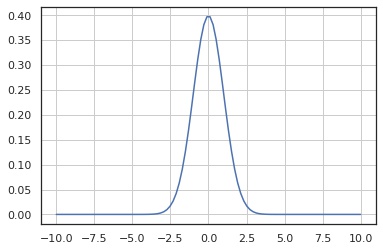

累積分布関数

In [4]: 
x = np.linspace(-10, 10, 100)
y = X.cdf(x)

fig, ax = plt.subplots()
ax.plot(x, y)
ax.grid()

plt.show()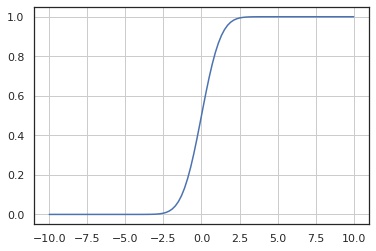

統計量

In [5]: 
print("mean", X.mean())
print("var", X.var())
print("std", X.std())
mean 0.0
var 1.0
std 1.0