概要
ディープラーニングの最適化に使用されるアルゴリズムである確率的勾配降下法について解説します。
勾配降下法
確率的勾配降下法は勾配降下法が元になっています。勾配降下法については以下の記事を参照してください。
[blogcard url=”https://pystyle.info/ml-gradient-descent”]
アルゴリズム 最急降下法
- 初期値 $\boldsymbol{w}_0$ を決める。
- 勾配 $\nabla f (\boldsymbol{w}_t; \boldsymbol{x})$ を計算し、$\nabla f (\boldsymbol{w}_t; \boldsymbol{x}) = \boldsymbol{0}$ の場合、終了する。
点を次のように更新する。
$$ \boldsymbol{w}_{t + 1} = \boldsymbol{w}_t -\alpha \nabla f (\boldsymbol{w}_t; \boldsymbol{x}) $$
2 に戻る。
確率的勾配降下法
データセットを $\mathbf{x} = (x_1, x_2, \cdots, x_n)$、最適化対象のパラメータを $\mathbf{w}$ としたとき、目標関数 $f(\mathbf{w}; \mathbf{x})$ が以下のように各サンプルから計算される関数 $f_i(\mathbf{w};x_i)$ の和の形で表せる場合を対象とします。
$$ f(\mathbf{w}; \mathbf{x}) = \sum_{i = 1}^N f_i(\mathbf{w};x_i) $$例えば、最小二乗誤差はサンプル $x_i$ に対応する正解を $y_i$、パラメータで表される関数の形状 (例 $g(x) = ax + b$) を $g(x)$ としたとき、
$$ f(\mathbf{w}; \mathbf{x}) = \frac{1}{N} \sum_{i = 1}^N (g(\mathbf{w}; x_i) – y_i)^2 $$と和で表す形になっています。
確率的勾配降下法は、すべてのサンプルを使って損失を計算する代わりに、ランダムに選んだサンプル1つで計算した $f_i$ の勾配でパラメータを更新します。
アルゴリズム 確率的最急降下法
- 初期値 $\boldsymbol{w}_0$ を決める。
- サンプルの1つ $x_i$ をランダムに選ぶ。
- 勾配 $\nabla f_i(\boldsymbol{w}_t;x_i)$ を計算する。
点を次のように更新する。
$$ \boldsymbol{w}_{t + 1} = \boldsymbol{w}_t -\alpha \nabla f_i(\boldsymbol{w}_t; x_i) $$
2 に戻る。
確率的勾配降下法の実装例
データセット $(x_1, y_1), (x_2, y_2), \cdots, (x_N, y_N)$ で関数 $g(x) = a x + b$ のパラメータを二乗誤差を最小化することで求めます。
二乗誤差は以下のように計算できます。
$$ f(\mathbf{w}; \mathbf{x}) = \frac{1}{N} \sum_{i = 1}^N (g(x_i) – y_i)^2 $$- 初期値 $a_0, b_0$ を決める。
- サンプルの1つ $x_i, y_i$ をランダムに選ぶ。
- 勾配 $\nabla (g(x_i) – y_i)^2$ を計算する。
点を次のように更新する。
$$ a_{t + 1} = a_t -\alpha \frac{\partial}{\partial a} \frac{1}{N} (g(x_i) – y_i)^2 = a_t -\alpha \frac{2}{N} (g(x_i) – y_i) x_i $$
$$ b_{t + 1} = b_t -\alpha \frac{\partial}{\partial b} \frac{1}{N} (g(x_i) – y_i)^2 = b_t -\alpha \frac{2}{N} (g(x_i) – y_i) $$
2 に戻る。
import matplotlib.pyplot as plt
import numpy as np
np.random.seed(0)
def g(x, a, b):
return a * x + b
# g(x) = 6x + 2 でデータを作成する。
a_true, b_true = 6, 2
xs = np.arange(-10, 10)
ys = g(xs, a_true, b_true)
def get_sample():
"""ランダムにサンプルを1つ選択する。"""
i = np.random.randint(len(xs))
return xs[i], ys[i]
a, b = 3, 8 # パラメータの初期値
lr_a, lr_b = 0.1, 2
max_steps = 50 # 反復回数
history = [(a, b)]
for _ in range(max_steps):
# ランダムにサンプルを選ぶ。
x, y = get_sample()
a -= lr_a * 2 / len(xs) * (g(x, a, b) - y) * x
b -= lr_b * 2 / len(xs) * (g(x, a, b) - y)
history.append((a, b))
history = np.array(history)
print(f"Optimization is complete. a={a:.6f}, b={b:.6f}")Optimization is complete. a=6.006183, b=2.033849
# 損失関数 MSE (\sum_{i = 0}^N (ax + b - y)^2) の形状をプロットする。
A, B = np.mgrid[:11, :11]
Y = np.square(A[..., np.newaxis] * xs + B[..., np.newaxis] - ys).mean(axis=-1)
def draw_history(A, B, Y, history, elev=70, azim=-70):
fig = plt.figure(figsize=(14, 6))
fig.suptitle("MSE Loss", fontsize=16)
# 勾配のベクトル図を作成する。
ax1 = fig.add_subplot(121)
ax1.grid()
ax1.set_title("Contour")
ax1.set_xlabel("$a$", fontsize=15)
ax1.set_ylabel("$b$", fontsize=15)
ax1.plot(history[:, 0], history[:, 1], "ro-", mec="b", mfc="b", ms=4)
contours = ax1.contour(A, B, Y, levels=15)
ax1.clabel(contours, inline=1, fontsize=10, fmt="%.2f")
# グラフを作成する。
ax2 = fig.add_subplot(122, projection="3d")
ax2.set_title("Surface")
ax2.set_xlabel("$a$", fontsize=15)
ax2.set_ylabel("$b$", fontsize=15)
ax2.set_zlabel("$loss$", fontsize=15)
ax2.plot(history[:, 0], history[:, 1], "ro-", mec="b", mfc="b", ms=4)
ax2.plot_surface(A, B, Y, alpha=0.3, edgecolor="black")
ax2.view_init(elev=elev, azim=azim)
plt.show()
draw_history(A, B, Y, history)
print(history[-1])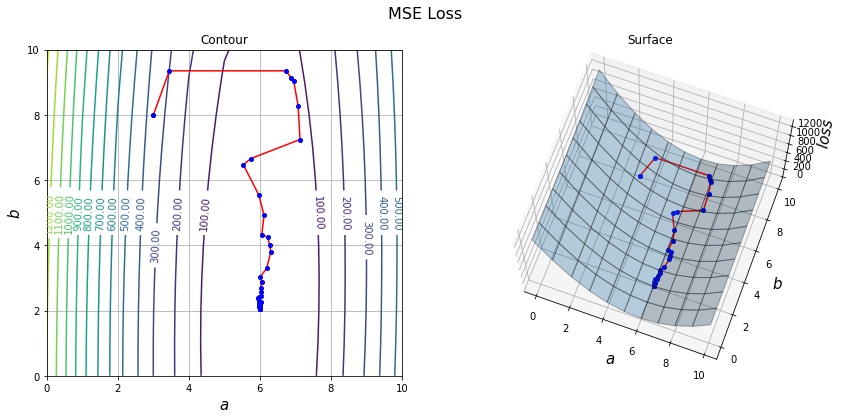
[6.00618334 2.0338487 ]
ミニバッチ勾配降下法
ミニバッチ勾配降下法は、すべてのサンプルを使って損失を計算する代わりに、ランダムに選んだ $b$ 個のサンプルで計算した勾配でパラメータを更新します。1個のサンプルで計算する勾配よりデータすべての勾配に近づくので、収束が早くなります。
アルゴリズム 確率的最急降下法
- 初期値 $\boldsymbol{w}_0$ を決める。
- $b$ 個のサンプルをランダムに選ぶ。
- 勾配 $\nabla \sum_{x \in batch} f_i(\boldsymbol{w}_t;x)$ を計算する。
点を次のように更新する。
$$ \boldsymbol{w}_{t + 1} = \boldsymbol{w}_t -\alpha \nabla \sum_{x \in batch} f_i(\boldsymbol{w}_t;x) $$
2 に戻る。
import matplotlib.pyplot as plt
import numpy as np
np.random.seed(0)
def g(x, a, b):
return a * x + b
# g(x) = 6x + 2 でデータを作成する。
a_true, b_true = 6, 2
xs = np.arange(-10, 10)
ys = g(xs, a_true, b_true)
def get_sample(batch_size):
"""ランダムにサンプルを1つ選択する。"""
i = np.random.randint(len(xs), size=batch_size)
return xs[i], ys[i]
a, b = 3, 8 # パラメータの初期値
lr_a, lr_b = 0.01, 0.1
max_steps = 50 # 反復回数
history = [(a, b)]
for _ in range(max_steps):
# ランダムにサンプルを選ぶ。
x, y = get_sample(10)
a -= lr_a * 2 / len(xs) * ((g(x, a, b) - y) * x).sum()
b -= lr_b * 2 / len(xs) * (g(x, a, b) - y).sum()
history.append((a, b))
history = np.array(history)
print(f"Optimization is complete. a={a:.6f}, b={b:.6f}")
draw_history(A, B, Y, history)
print(history[-1])Optimization is complete. a=6.000140, b=2.037621
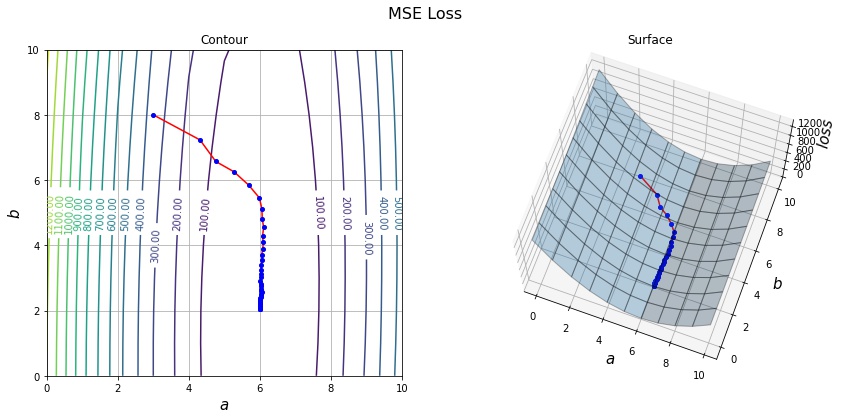
[6.00014004 2.03762096]










コメント