Warning: Undefined variable $position in /home/pystyles/pystyle.info/public_html/wp/wp-content/themes/lionblog/functions.php on line 4897
  1. HOME
  2. 機械学習
  3. 機械学習 - 棄却オプション

機械学習 – 棄却オプション

機械学習 – 棄却オプション
目次

概要

決定理論における棄却オプションについて解説します。

Advertisement

棄却オプション

誤り率 $\varepsilon(\bm{x})$ が一定の値より大きい領域では判断を避けることを棄却オプション (reject option) といいます。 棄却する領域は

$$ L_R(t) = \{ \bm{x} \in \R^d \mid \varepsilon(\bm{x}) \ge t \} $$

と表せます。

最尤識別規則の場合の棄却オプション

棄却領域

最尤識別規則の場合の棄却領域は

$$ \begin{aligned} L_R(t) &= \{ \bm{x} \in \R^d \mid \varepsilon(\bm{x}) \ge t \} \\ &= \{ \bm{x} \in \R^d \mid 1 – \max_i p(\bm{x}|c_i) \ge t \} \\ &= \{ \bm{x} \in \R^d \mid \max_i p(\bm{x}|c_i) \le 1 – t \} \\ \end{aligned} $$

2クラス分類の場合の棄却領域

釣った魚の大きさが $x \in \R$ であったとき、その魚が鮭 (salmon)、スズキ (sea bass) のどちらであるかを識別する2クラス分類問題を考えます。(鮭、スズキ以外の魚が釣れることはないと仮定します)

以下の情報がわかっているものとします。

  • 鮭の大きさは正規分布 $\mathcal{N}(5, 1)$ に従う $$ p(x|salmon) = \frac{1}{\sqrt{2 \pi}} \exp \left( -\frac{(x – 5)^2}{2} \right) $$
  • スズキの大きさは正規分布 $\mathcal{N}(10, 4)$ に従う $$ p(x|bass) = \frac{1}{2 \sqrt{2 \pi}} \exp \left( -\frac{(x – 10)^2}{8} \right) $$

このとき、棄却領域は

$$ \begin{aligned} L_R &= \{ \bm{x} \in \R^d \mid 1 – \max(p(x|salmon), p(x|bass)) \ge t \} \\ &= \{ \bm{x} \in \R^d \mid \max(p(x|salmon), p(x|bass)) \ge 1 – t \} \end{aligned} $$

棄却オプションの閾値を $t = 0.9$ として、グラフを描画します。

In [1]: 
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm

x = np.linspace(0, 20, 100)

salmon_y1 = norm.pdf(x, loc=5, scale=1)
bass_y1 = norm.pdf(x, loc=10, scale=2)
error = 1 - np.maximum(salmon_y1, bass_y1)
t = 0.9

fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(9, 12))
ax1.plot(x, salmon_y1, "b", label=r"$p(x|salmon)$")
ax1.plot(x, bass_y1, "g", label=r"$p(x|bass)$")
ax1.axhline(1 - t, color="k", ls="--")
ax1.text(0, 1 - t + 0.01, f"$1 - t={1 - t:.1f}$", fontsize=16)
ax1.set_xlabel("Length")
ax1.grid()
ax1.legend()

ax2.plot(x, error, "r", label=r"$\varepsilon(x)$")
ax2.axhline(t, color="k", ls="--")
ax2.text(0, t + 0.01, f"$t={t:.1f}$", fontsize=16)
ax2.set_xlabel("Length")
ax2.grid()
ax2.legend()

plt.show()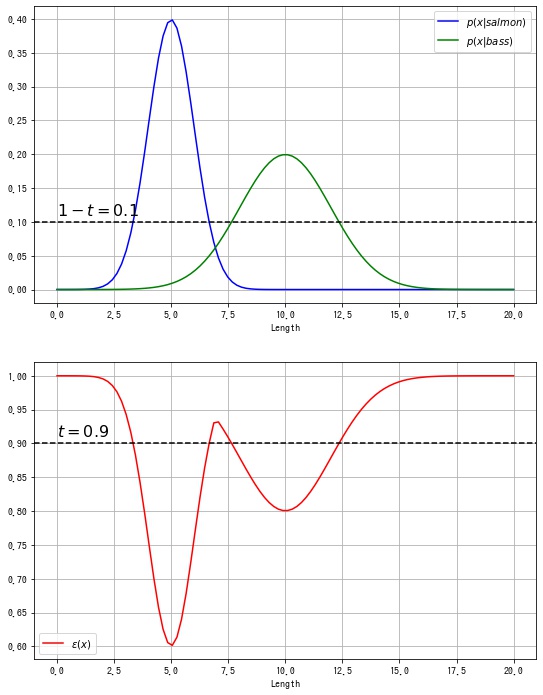

Sympy で $\max(p(x|salmon), p(x|bass)) = 1 – t$ を解いて、棄却領域の範囲を計算します。

In [2]: 
import sympy as sym
from sympy.stats import density, Normal

x = sym.symbols("x")

salmon_pdf = density(Normal("salmon", 5, 1))(x)
bass_pdf = density(Normal("bass", 10, 2))(x)
t = 0.9

# 方程式を解く。
sol = []
ret = sym.solve(salmon_pdf - (1 - t))
sol += list(map(sym.N, ret))

ret = sym.solve(bass_pdf - (1 - t))
sol += list(map(sym.N, ret))

for x in sol:
    print(f"{x:.2f}", end=" ")
3.34 6.66 7.65 12.35

棄却領域は $L_R = [-\infty, 3.34] \cup [6.66, 7.65] \cup [12.35, \infty]$ とわかりました。

最尤識別規則の棄却領域

Advertisement

最大事後確率識別規則の場合の棄却オプション

棄却領域

最尤識別規則の場合の棄却領域は

$$ \begin{aligned} L_R(t) &= \{ \bm{x} \in \R^d \mid \varepsilon(\bm{x}) \ge t \} \\ &= \{ \bm{x} \in \R^d \mid 1 – \max_i p(c_i|\bm{x}) \ge t \} \\ &= \{ \bm{x} \in \R^d \mid \max_i p(c_i|\bm{x}) \le 1 – t \} \\ \end{aligned} $$

2クラス分類の場合の棄却領域

釣った魚の大きさが $x \in \R$ であったとき、その魚が鮭 (salmon)、スズキ (sea bass) のどちらであるかを識別する2クラス分類問題を考えます。(鮭、スズキ以外の魚が釣れることはないと仮定します)

以下の情報がわかっているものとします。

  • 事前確率
    • 釣った魚が鮭である確率は $p(salmon) = \frac{2}{3}$
    • 釣った魚がスズキである確率は $p(bass) = \frac{1}{3}$
  • 尤度
    • 鮭の大きさは正規分布 $\mathcal{N}(5, 1)$ に従う $$ p(x|salmon) = \frac{1}{\sqrt{2 \pi}} \exp \left( -\frac{(x – 5)^2}{2} \right) $$
    • スズキの大きさは正規分布 $\mathcal{N}(10, 4)$ に従う $$ p(x|bass) = \frac{1}{2 \sqrt{2 \pi}} \exp \left( -\frac{(x – 10)^2}{8} \right) $$

このとき、棄却領域は

$$ \begin{aligned} L_R &= \{ \bm{x} \in \R^d \mid 1 – \max(p(salmon|x), p(bass|x)) \ge t \} \\ &= \{ \bm{x} \in \R^d \mid \max(p(salmon|x), p(bass|x)) \le 1 – t \} \end{aligned} $$

棄却オプションの閾値を $t = 0.95$ として、グラフを描画します。

In [3]: 
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm

x = np.linspace(0, 20, 100)

salmon_y1 = norm.pdf(x, loc=5, scale=1) * 2 / 3
bass_y1 = norm.pdf(x, loc=10, scale=2) * 1 / 3
error = 1 - np.maximum(salmon_y1, bass_y1)
t = 0.95
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(9, 12))
ax1.plot(x, salmon_y1, "b", label=r"$p(salmon|x)$")
ax1.plot(x, bass_y1, "g", label=r"$p(bass|x)$")
ax1.axhline(1 - t, color="k", ls="--")
ax1.text(0, 1 - t + 0.01, f"$1 - t={1 - t:.2f}$", fontsize=16)
ax1.set_xlabel("Length")
ax1.grid()
ax1.legend()

ax2.plot(x, error, "r", label=r"$\varepsilon(x)$")
ax2.axhline(t, color="k", ls="--")
ax2.text(0, t + 0.01, f"$t={t:.2f}$", fontsize=16)
ax2.set_xlabel("Length")
ax2.grid()
ax2.legend()

plt.show()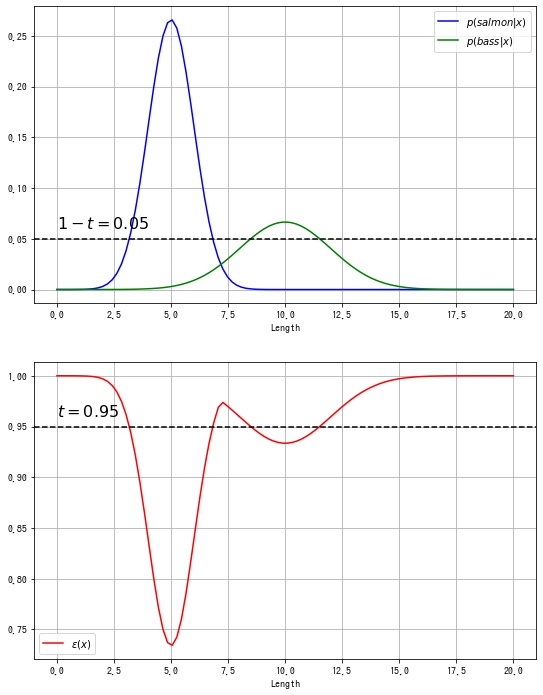

Sympy で $\max(p(salmon|x), p(bass|x)) = 1 – t$ を解いて、棄却領域の範囲を計算します。

In [4]: 
import sympy as sym
from sympy.stats import density, Normal

x = sym.symbols("x")

salmon_pdf = density(Normal("salmon", 5, 1))(x) * 2 / 3
bass_pdf = density(Normal("bass", 10, 2))(x) * 1 / 3
t = 0.95

# 方程式を解く。
sol = []
ret = sym.solve(salmon_pdf - (1 - t))
sol += list(map(sym.N, ret))

ret = sym.solve(bass_pdf - (1 - t))
sol += list(map(sym.N, ret))

for x in sol:
    print(f"{x:.2f}", end=" ")
3.17 6.83 8.49 11.51

棄却領域は $L_R = [-\infty, 3.17] \cup [6.83, 8.49] \cup [11.51, \infty]$ とわかりました。

MAP 識別規則の棄却領域